§ 2. Примеры математических теорий из алгебры, анализа, геометрии

1. Теория частичного упорядочения.

Пусть теория Т содержит одну предикатную букву и не содержит функциональных букв и предметных констант. Вместо формул и обычно пишут х₁ < х₂ и х₁ не < х₂ .

Пусть Т содержит две специальные аксиомы:

а) ( ) – иррефлективность;

б)  – транзитивность.

Всякая модель этой теории называется частично упорядоченной структурой.

2. Теория групп.

Пусть теория Т содержит одну предикатную букву , одну функциональную букву и одну предметную константу а₁. Пользуясь принятыми в алгебре обозначениями, будем писать:

t = s вместо (t, s),

t + s вместо (t,s),

0 вместо а₁.

Специальными аксиомами теории Т здесь являются формулы:

а) – ассоциативность;

б) – свойство нуля;

в) – существование обратного элемента;

г) – рефлексивность равенства;

д) – симметричность равенства;

е) – транзитивность равенства;

ж) –

подстановочность равенства.

Всякая модель этой теории называется группой. Если в группе истинна формула , то группа называется абелевой или коммутативной. Примерами групп являются:

1. множество всех взаимно однозначных отображений множества М на себя, рассматриваемое вместе с операцией суперпозиции отображений;

2. множество Z всех целых чисел, рассматриваемое вместе с операцией сложения целых чисел;

з) множество V₂ всех векторов плоскости, рассматриваемое вместе с операцией сложения векторов по правилу треугольника или параллелограмма;

4. пространство R₂ⁿ всех векторов n-мерного пространства с операцией сложения векторов, определяемой как покоординатное сложение;

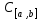5. –пространство непрерывных на [a,b] функций с нормой 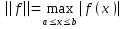и обычной операцией сложения.

Теория частичного упорядочения и теория групп являются эффективно аксиоматизированными, то есть имеется возможность для любой данной формулы эффективно выяснить, принадлежит ли она к числу логических аксиом.

3. Аффинная геометрия.

Первичными терминами этой теории являются: множество Р (элементы которого, называемые точками, будут обозначаться прописными латинскими буквами Р, Q, ...), множество L (элементы которого, называемые прямыми, будут обозначаться строчными латинскими буквами l, т, ...) и множество J, называемое отношением инцидентности.

Специальными аксиомами теории Т здесь являются формулы:

а) J  РL (< Р,l > J) читается «Р лежит на l», или « l содержит Р», или «l проходит через Р», или «Р и l инцидентны».

б) Для любых двух различных точек Р и Q существует в точности одна прямая, проходящая через Р и Q. Будем обозначать такую прямую через P + Q.

в) Для любой точки Р и любой прямой l существует в точности одна прямая m, проходящая через Р и параллельная прямой l (т.е. либо т = l, либо не существует точек, лежащих на обеих прямых l и т).

г) Если А, B, С, D, Е, и F – шесть различных точек, причем А + В параллельна С + D , С + D параллельна .Е + F, А + С параллельна В + D и С + E параллельна D + Е, то А + Е параллельна и B + F.

д) Существует три различных точки, не лежащие на одной прямой.

4. Геометрия (теория равенства отрезков).

Первичные термины: множество S – множество всех отрезков, и «=» – отношение равенства, так что выражение «х = у» читается так: «отрезок х равен отрезку у». Специальные аксиомы:

а) ;

б) .

5. Аксиоматическая теория натуральных чисел (построенная итальянским математиком Дж.Пеано).

Первоначальные понятия: непустое множество N, отношение следования « ' » и выделенный элемент 1. Специальные аксиомы:

а)N (x1);

б) N (x=yx=y);

в) N (x=yx=y);

г) Пусть M  N. Тогда (l  M)(М  xМ)M=N.

Доказательство в теории есть способ обоснования истинности некоторого суждения. В математике, для которой характерен аксиоматический метод, взгляд на доказательство определяется взглядом на аксиоматическую теорию. Слово «теория» понимается здесь в определенном специальном смысле. Термин «теория» применяют по отношению к двум множествам высказываний, одно из которых есть собственное подмножество другого. Большое (объемлющее) множество высказываний определяет предметную область теории, элементы же меньшего (охватывающего) множества высказываний – это высказывания теории, которые считаются в ней истинными или доказуемыми (или теоремами). Они определяются как высказывания, выводимые чисто логическим путем из некоторых заранее выбранных и фиксированных высказываний, называемых аксиомами.

В аксиоматической теории понятию истинности нет места – понятие истинного высказывания имеет смысл лишь в связи с возможными приложениями теории.

Определение 1 (доказательства). Доказательством называют конечную последовательность s₁, s₂, ..., s_k высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода.

Определение 2 (теоремы). Теоремой или доказуемым высказыванием называется высказывание, являющееся последним высказыванием некоторого доказательства.

Ясно, что любая аксиома является теоремой, причем ее доказательство состоит из одного шага.

Вывод высказывания С из пустого множества посылок есть, очевидно, доказательство высказывания С.

Теорема. Если формула А теории первого порядка Т есть частный случай тавтологии, то А есть теорема в Т и может быть выведена с употреблением схем логических аксиом (1), (2) и (3) и правила заключения.

Доказательство. Пусть формула А получена из некоторой тавтологии В с помощью подстановок, и x₁, x₂, ..., х_n – набор переменных, входящих в В. Как известно, в этом случае существует вывод В из совокупности . Сделаем в этом выводе всюду подстановки по следующим правилам:

1. если какая-нибудь переменная x_i входит в В, то на места всех ее вхождений в каждую формулу вывода подставляем ту формулу теории Т, которая подставлялась в В на места вхождения той же буквы при построении А.

2. если некоторая переменная x_k не входит в В, то на места всех ее вхождений в формулы вывода подставляет произвольную (одну и ту же для данной буквы) формулу теории Т.

Полученная таким образом последовательность формул и будет выводом формулы А в теории Т. При этих рассуждениях использовались только аксиомы (1), (2), (3) и правило заключения.

Как известно, в исчислении высказываний справедлива Теорема дедукции:

Если Н, С ├ А, то Н ├ СА.

Эта теорема без соответствующих изменений не справедлива для произвольных теорий первого порядка Т. Например, в любой теории первого порядка всегда

А ├ , но не всегда доказуема формула А. Действительно, рассмотрим область, содержащую по крайней мере два элемента М = а, в, ...}.

Пусть Т – исчисление предикатов, и пусть формула А есть . Проинтерпретируем каким-нибудь свойством, которым обладает только элемент а. Тогда выполнима на множестве, которое содержит а, при этом формула не выполнима на множестве М.