§ 1. Теории первого порядка. Основные понятия

Определим язык теории первого порядка.

Определение 1. Алфавитом А называется всякое непустое конечное множество символов. Символы алфавита называются буквами.

Определение 2. Словом в алфавите А называется всякая конечная последовательность букв алфавита А. Пустая последовательность букв называется пустым словом и обозначается через А.

Будем говорить, что два конкретных слова a₁a₂...а_п и b₁b₂...b_k алфавита А равны и писать а₁а₂... а_п = b₁b₂...b_k, если п = k и a₁ = b₁, а₂ = b₂, ..., а_п =b_п. При этом число п называют длиной этого слова.

Пусть Т – некоторая теория. Обозначим через А(Т) алфавит этой теории. Множество Е(Т) слов алфавита А(Т) называют множеством выражений теории Т.

Пару (А(Т), Е(Т)), состоящую из алфавита А(Т) и множества выражений Е(Т) теории Т называют языком теории Т.

Языки первого порядка обслуживают теории первого порядка. В алфавит всякой теории Т первого порядка входят по существу те же символы, которые были введены ранее. Это символы логических операций , , , –; символы кванторных операций , ; вспомогательные символы – скобки, запятые; счетное множество n-местных предикатных букв (n,j  l), где верхний индекс указывает на число мест, а нижний – номер предикатной буквы; конечное (возможно, и пустое) или счетное множество функциональных букв (n,j  l), где верхний индекс указывает на число переменных, входящих в функцию, а нижний – номер функциональной буквы; конечное (возможно пустое) или счетное множество предметных констант а_i (i  l).

В частности, под функциональной буквой может пониматься цепочка логических операций.

Множество предикатных букв вместе с множеством функциональных букв и констант называется сигнатурой языка данной теории и является его специфической частью.

Таким образом, в теории Т первого порядка могут отсутствовать некоторые или даже все функциональные буквы и предметные константы, а также некоторые, но не все предикатные буквы.

Различные теории первого порядка могут отличаться друг от друга по составу букв в алфавите.

Определение терма.

1. Предметная переменная и предметная константа – термы.

2.Если r₁, r₂, ..., r_п – термы и А – символ n-местной операции, то (r₁, r₂, …, r_n) терм.

3. Никаких других термов, кроме определенных в п. 1 и п. 2, в Т нет.

Согласно естественной интерпретации, терм – это имя некоторого предмета. Кроме переменных и предметных констант, термами являются цепочки, образованные из переменных и предметных констант посредством символов операций, так как в подразумеваемой интерпретации он истолковывается как значение некоторой функции.

Определение формулы.

1. Если А – символ n-местного отношения (предикат или функция), а r₁, r₂, ..., r_п – термы, то A(r₁, r₂, ..., r_п) – формула. В частности, если А – предикатная буква , то (r₁, r₂, ..., r_п) называется элементарной формулой.

2. Если А и В формулы, то АВ, AВ, АВ , – формулы.

3. Если А – формула, а у – предметная переменная, которая входит в А свободно или не содержится в А, то выражения yA, уА – формулы. При этом А называется областью действия квантора.

4. Никаких других формул, кроме определенных в п. 1 – 3, нет.

Логические и специальные аксиомы. Правила вывода.

Аксиомы теории первого порядка Т разбиваются на два класса: логические аксиомы и специальные (нелогические или собственные аксиомы).

Логические аксиомы. Каковы бы ни были формулы А, В и С теории Т следующие формулы являются логическими аксиомами теории Т:

1. А(ВА);

2. (А(ВС))((АВ)(АС));

3. ;

4. , где есть формула теории Т и t есть терм теории Т, свободный в А(x_i). Отметим, что t может совпадать с х_i, и тогда мы приходим к аксиоме ;

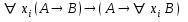1. 5. , если x_i не входит свободно в формулу А.

Замечание. Ранее в главе 2 было построено классическое исчисление высказываний, содержащее 11 аксиом. Однако может быть построено исчисление высказываний с меньшим числом аксиом (в частности, с логическими аксиомами 1) – 3).

Специальные аксиомы. Они не могут быть сформулированы в общем случае, так как меняются от теории к теории.

Теория первого порядка, не содержащая собственных аксиом, очевидно, представляет собой чисто логическую теорию. Она носит название исчисления предикатов первого порядка.

Во многих теориях, которые могут быть аксиоматизированы как теории первого порядка, используется понятие равенства. Оно вводится путем добавления двухместного предиката « х = у » и в связи с этим добавляются две специальные аксиомы: 1) x (х = х); 2) Если х, у, z – различные предметные переменные и F(z) – формула, то xy(x = yF(x) = F(y)).

Правила вывода. Как и в исчислении высказываний, будем пользоваться понятиями вывода из совокупности формул (высказываний) Н. Высказывания, входящие в Н, будем называть допущениями (или посылками). Если последним высказыванием в выводе из Н стоит высказывание А, то будем говорить, что предложение А выводимо из Н и записывать: Н├А. В частном случае, если Н = , то пишут ├А.

В число правил вывода теории первого порядка включаются два правила:

1. Правило заключения (или modus ponens):

Если ├ А и ├ АВ, то ├ В.

2. Правило связывания квантором всеобщности (или правило обобщения):

Если ├ А, то ├ .