892

А.Н. Колмогоров доказал, что при любой функции распределения F(x) и достаточно большом числе наблюдений, вероятность неравенства

Dmax 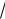n стремится к пределу:

k

При малых значениях вероятности Рλ гипотезу следует отвергать, а при достаточно большом – считать опытные данные не противоречащими выдвинутой гипотезе.

Наибольшая разность теоретического F(x) и фактического распределения в предыдущем примере составляет Dmax

В этом случае Dmax n 0,442 0,5 , что соответствует Рλ=0,964,

т.е. и по этому критерию опытные данные не противоречат гипотезе о показательном распределении времени обслуживания машин.

Проверка гипотез о параметрах распределения. Поскольку в каче-

стве основных параметров распределений случайных величин используют значения их математических ожиданий и дисперсий, то, прежде всего, важно сопоставить оценки этих числовых характеристик. Например, иногда результаты одной серии экспериментов значительно отличаются от результатов другой серии. Становится неясным, можно ли объяснить обнаруженное расхождение параметров случайными ошибками опыта или оно вызвано принадлежностью к различным закономерностям?

В некоторых случаях, особенно при испытаниях модернизированных рабочих органов, получают результаты, которые мало отличаются от соответствующих показателей базовых машин. В этом случае следует определить существенность различий оценок параметров исследуемых распределений. Проверку существенности различий оценок математического ожидания проводят с помощью t-критерия.

Для этого, прежде всего, определяют значение критерия:

характеристик соответственно первого и второго распределений; n1 и n2 – число измерений.

Затем по таблицам [38] находят критическое значение критерия Стьюдента в зависимости от числа степеней свободы k = n1+n2-2 и принятой доверительной вероятности β. Если t > tкр, то оценки математических ожиданий считают неоднородными, а при t < tкр разница между оценками несущественна.

Пример 1.

В опытах по фракционированию зерна после обмолота двухбарабанным комбайном проверена всхожесть семян. Результаты, полученные А.А.Майстренко, внесены в таблицу 7.8.

231

Таблица 7.8

Всхожесть семян, выделенных после первого и второго молотильного барабанов

Критическое значение tкр = 6,86 при доверительной вероятности β=0,999 и числе степеней свободы k = n – 1 = 6 – 1 = 5.

Поскольку t > tкр , то отличие во всхожести фракций семян следует считать существенным.

Пример 2.

Изучается величина потерь зерна за двумя вариантами молотильносепарирующих устройств конструкции ГСКБ Ростсельмаш.

Величина потерь представлена в таблице 7.9.

Таблица 7.9

Потери зерна за молотильно-сепарирующими устройствами

232

Усредненное значение среднеквадратического отклонения:

β=0,95 и числе степеней свободы (n-1)=3 [38].

Таким образом t > tкр, т.е. различие в величине потерь зерна за моло- тильно-сепарирующей частью исследуемых комбайнов существенно.

Пример 3.

Изучается расход топлива автомобиля Chevrolet Lacetti с рабочим объемом двигателя 1,4 л, в сравнении с ВАЗ-21043, имеющим объем двигателя 1,45 л.

Результаты измерений занесены в таблицу 7.10.

Таблица 7.10

Расход топлива двигателей автомобилей на 100 км пробега

Критическое значение tкрит = 2,26 при β=0,95 и k=n-1=10-1=9. Поскольку t < tкрит, то отличие в расходах топлива этих автомобилей

несущественно.

Существенность различий двух сравниваемых дисперсий проверяют

спомощью критерия Фишера (F-критерия):

~~

F x2 / y2 ,

где ~ и ~2 - соответственно, большее и меньшее значения сравни-

2

x y

ваемых дисперсий.

Далее по таблицам [38, 48, 56] находят критическое значение крите-

233

рия Фишера, соответствующее выбранному уровню риска α и числам сте-

пеней свободы k1 = n1 – 1 и k2 = n2 – 1. Если F < Fкр, то различие дисперсий считают несущественным.

Пример. В опытах В.С. Кирова (Пермская ГСХА) исследовано влияние постановки двухступенчатого ротора на разбрасывателе удобрений из куч РУН-Ф-15ВМ.

В результате полевых опытов получены следующие результаты. На серийном разбрасывателе с одноступенчатыми роторами:

среднее количество удобрений на 1 м2 - x1 =3 кг/м2; дисперсия D1=2,25; на экспериментальном разбрасывателе с двухступенчатым рото-

ром x2 = 2,9 кг/м2, D2 = 1,96.

Число измерений в каждом варианте n1 = n2 = 200. Величина F-критерия оказывается равной:

F D1 2,25 1,15 . D2 1,96

Критическое значение критерия для 1%-го уровня риска составляет

Fкр=1,39.

Поскольку F < Fкр, то постановка ступенчатого ротора в данной серии опытов существенного влияния на равномерность распределения органических удобрений не оказала.

Если необходимо проверить гипотезы об однородности некоторого ряда дисперсий (например, при нескольких последовательных выборках), используют критерий Кохрена (если число измерений одинаково) или Бартлета (если числа элементов в выборках различные).

Критерий Кохрена вычисляют по формуле:

где ~ - максимальное значение сравниваемых дисперсий.

2

max

Критическое значение этого критерия находят по таблицам [48] с учетом принятого уровня риска, числа степеней свободы n - 1 и сравниваемых дисперсий.

Если G > Gкр, то различие дисперсий существенно, а при G < Gкр ряд сравниваемых дисперсий считают однородным.

Проверка гипотез о принадлежности к выборке. Если при обработке опытных данных возникает сомнение в некоторых числах (например, они резко отличаются от остальных измерений), то их проверяют на несоответствие («на промах») с помощью критериев Грэбса-Смирнова (V-критерий) и Ирвина.

Схема использования V-критерия состоит в следующем. По результа-

~

там измерений, в том числе и по считающимся ошибочным, определяют x

~

и .

234

Затем, в зависимости от того, какое из экстремальных значений (хmax

После этого по таблице V-критерия [48], в зависимости от принятого уровня риска и числа измерений n, находят значение Vmax, при котором результат измерения хmax и хmin можно считать следствием статистического разброса величины хi.

Когда V < Vmax, подозреваемое измерение нужно сохранить, а при V>Vmax его можно исключить из анализа как ошибочное.

Пример.

Произведено испытание образцов металлокерамики, пропитанной медью, предназначенных для изготовления антифрикционных накладок.

Результаты измерений представлены в таблице 7.11.

Таблица 7.11

Результаты испытаний образцов, пропитанных медью

235

Критическое значение критерия при n = 8 и α = 0,01, равно

Vкр 2,4.

Поскольку V < Vкрит, то результаты измерений 6-го образца не являются грубой ошибкой, их нужно сохранить в расчетах.

Если используют критерий Ирвина, все результаты измерения выстраивают в ранжированный ряд (обычно в порядке уменьшения). Затем считающийся ошибочным (подозреваемый «на промах») результат сравни-

вают с соседним значением ряда, вычисляя при этом критерий Ирвина:

~

хmax xпред,max / .

После этого по таблице критерия Ирвина [48] находят критическое значение критерия в зависимости от числа измерений и принятой доверительной вероятности β. Если кр , то подозреваемый результат отбрасы-

вают, а при кр – сохраняют.

Пример.

При определении времени безотказной работы машины выявлено, что после ранжирования ряд оказался следующим (час):

х 85; 70; 62; 60; 58; 55; 52; 50; 47; 45.

Среднее значение времени безотказной работы составит:

Дисперсия этого ряда равна D = 141,3 ч2, а среднеквадратическое отклонение = 11,84 ч.

Значение критерия Ирвина окажется равным:

Критическое значение критерия при n = 10 и доверительной вероятности β = 0,99 равно λкр = 2. Таким образом, λ < λкр и подозреваемое на грубую ошибку значение хmax = 85 ч нужно сохранить.

7.5. Оценки систем случайных величин

В практике работы со случайными величинами достаточно часто приходится сталкиваться с задачами, в которых результат опыта зависит не от одной, а от двух или более случайных величин, образующих комплекс или систему.

Например, при оценке равномерности распределения семян и удобрений по площади питания приходится учитывать и абсциссу, и ординату расположения частиц как систему случайных величин.

Свойства системы нескольких случайных величин не исчерпываются характеристиками отдельных величин, ее составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами.

Вероятностная или «стохастическая» зависимость означает, что изменение одной величины из системы более или менее влияет на вероят-

236

ностные характеристики другой.

Ранее уже было отмечено, что отдельно взятая случайная величина может быть охарактеризована начальными

ms[ X ] M[ X s ]

или центральными моментами

s[ X ] M[ X s ] M[ x mx s ] ,

где mх – математическое ожидание случайной величины Х.

Из этих характеристик важнейшими являются математическое ожидание mx и дисперсия Dx:

s X Dx M X 2 .

Система случайных величин характеризуется [56] начальным мо-

т.е. математическое ожидание произведения центрированных величин. Ввиду того, что этот момент играет важную роль в теории систем

случайных величин, для него введено особое обозначение:

где ζх, ζy – средние квадратические отклонения величин х и у.

Корреляция может быть положительной (когда с ростом х увеличивается у) и отрицательной (когда с ростом х, у – уменьшается). Коэффициент корреляции характеризует линейную зависимость х и у.

237

Статистическая оценка коэффициента корреляции

При вычислении коэффициента корреляции r опытные данные обычно сводят в таблицу со значениями х и у.

При использовании данных таблицы коэффициент корреляции вычисляют в следующем порядке.

1. Определяют средние арифметические значения Х и Y:

2. Вычисляют выборочный корреляционный момент:

3.Определяют скорректированные дисперсии и средние квадратические отклонения величин X и Y:

4. Вычисляют оценку коэффициента корреляции; r Kxy / x y .

Пример: Используя данные испытаний отечественных и зарубежных комбайнов на МИС АПК, в ГОСНИТИ проанализирована зависимость их производительности (т/ч) от мощности двигателя N, кВт.

Среди 9 исследованных комбайнов «Нива-эффект», «Вектор», «Век- тор-410», «Акрос-530», «Енисей КЗС-950», КЗС-1218 (Брянсксельмаш) и 3

комбайна фирм «John Deer» и Claas (LEXION-580 и Tucano-540).

Результаты испытаний внесены в таблицу 7.12.

Таблица 7.12

Зависимость производительности зерноуборочных комбайнов (yi) от мощности двигателя (xi)

238

Вычисленные характеристики:

Значимость выборочного коэффициента корреляции r проверяют с помощью нулевой гипотезы r = 0, т.е. с помощью гипотезы о том, что изучаемые признаки X и Y генеральной совокупности не связаны между собой линейной зависимостью. Отбрасывание нулевой гипотезы будет свидетельствовать о том, что полученный коэффициент корреляции r достоверен.

Нулевую гипотезу Н0 можно проверить с помощью критерия Стьюдента со степенями свободы k = N – 2

При |t| ≥ t2|2 гипотезу Н0 отвергают.

Критическое значение критерия t при α = 0,05 и k = 7 будет t = 2,36. Поскольку 7,29 > 2,36, то вычисленное значение r достоверно.

Коэффициент корреляции указывает на направление и степень сопряженности в изменении признаков, но не позволяет судить о том, как количественно меняется результативный признак при изменении факториального на единицу измерения, что нередко важно в познавательных и практических целях. В подобных случаях на помощь приходит регрессионный анализ.

Под регрессией понимают изменение результативного признака, называемого зависимой переменной, или функцией Y, при определенных изменениях факториального признака, называемого независимой переменной, или аргументом Х.

По форме регрессия может быть прямолинейной и криволинейной. Прямолинейная регрессия – это такая зависимость, когда при любом значе-

239

нии аргумента одинаковые приращения его вызывают одинаковые приращения функции, криволинейная – когда при одинаковых приращениях аргумента функция имеет неодинаковые приращения.

Регрессия называется простой, если изменение функции исследуется от одного аргумента [y = f(x)], и множественной – от двух и более аргумен-

тов [y= f(x1,x2,x3…)].

Зависимость функции от аргумента при линейной регрессии может быть выражена коэффициентом регрессии. Коэффициентом линейной регрессии называется число, показывающее, в каком направлении и на какую величину изменяется один признак (функция) при изменении другого (аргумента) на единицу измерения.

Обычно обозначают коэффициент регрессии буквой b и вычисляют по формулам:

Коэффициент регрессии byx показывает, как меняется Y при изменении Х на единицу измерения и выражается в единицах Y; a bxy указывает регрессию Х на Y и выражается в единицах X (что, впрочем, не всегда имеет логический смысл, например, урожай может зависеть от количества осадков, а осадки от урожая, как известно, не зависят).

Коэффициенты линейной регрессии имеют знак коэффициента корреляции.

Произведение коэффициентов регрессии равно квадрату коэффициента корреляции:

byx bxy r 2 .

Этой формулой можно пользоваться как проверочной при вычислении коэффициентов регрессии.

Среднеквадратическую ошибку коэффициентов регрессии вычисляют по формулам:

3,55 0,05x .

Уравнение регрессии позволяет определить производительность комбайна с тем или иным двигателем.

Например, если х = 200, то у = 3,55+10 = 13,55 т/ч.

Очень часто причиной изменчивости тех или иных элементов техно-

240