892

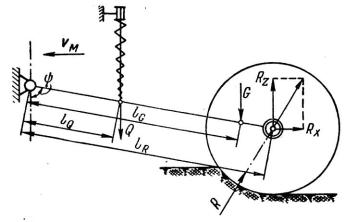
Но на систему наложено пять связей, уравнения которых имеют вид:

х0=0; у0=0; х12 у12 l12 ; x2 x1 2 y2 y1 2 l22 ; у2=0.

Независимой остается лишь одна из шести координат. За обобщенную координату можно принять любую из трех координат х1; у1; х2, у2, но удобнее взять угол поворота кривошипа θ, так как через него легко выразить все остальные координаты.

В современной практике моделирования [17] в качестве обобщенных координат рекомендуются величины, производные по времени, от которых представляют фазовые координаты типа потока (скорости, расходы, температуры, токи).

Производные от обобщенных координат qi называют обобщенными скоростями qi . В механических системах обобщенными могут быть ли-

нейные или угловые скорости.

Одновременное задание всех координат и скоростей полностью определяет состояние системы и позволяет в принципе ее дальнейшее движение. С математической точки зрения это значит, что заданием всех координат qi, и скоростей qi в некоторый момент времени однозначно опреде-

ляется также и значение ускорений qi в этот момент.

Обобщенные силы. Каждой обобщенной координате qi соответствует своя обобщенная сила Qi.

Работу всех обобщенных сил на возможных перемещениях системы (виртуальную работу) можно вычислить по формуле:

i 1

где δqi – вариация i-той обобщенной координаты;

δАi – работа i-й обобщенной силы на возможном перемещении.

Из этой формулы следует, что обобщенные силы представляют собой коэффициенты при вариациях обобщенных координат в выражении для виртуальной работы.

Так как вариации обобщенных координат δqi независимы, то вычисляя работу всех приложенных к системе сил на одном из возможных перемещений δqi, а все остальные вариации в формуле (5.21) полагая равными нулю, легко определить каждую обобщенную силу Qi в отдельности.

Из этой же формулы получают размерность обобщенной силы [Q]=[A]/[q]. Так, если обобщенная координата имеет размерность длины, то обобщенная сила имеет размерность силы (Н), если же обобщенной координатой является угол, то обобщенная сила имеет размерность момента

(Н м).

В гидравлических, тепловых или электрических системах размерность обобщенных сил может быть иной, связанной с физической размерностью гидравлических или тепловых потоков, электромагнитных моментов и др. Обобщенные силы часто подразделяют на произвольные (внешние,

активные), потенциальные (консервативные) и диссипативные (рассеива-

ющие). Такая классификация обычно связана с выделением из моделируе-

101

мого технического объекта типовых элементов. К ним относят завершенные в конструктивном отношении узлы, предназначенные для выполнения определенных функций и обладающие своеобразными динамическими свойствами. Примерами таких элементов являются инерционные (обычно сосредоточенные массы, обладающие свойством накапливать кинетическую энергию); упругие (способные накапливать потенциальную энергию); диссипативные (отображающие свойства диссипации (рассеяния) энергии конструктивными элементами технического объекта, обусловленные силами внутреннего трения); фрикционные (отражающие свойства фрикционных механизмов); трансформаторные (отображающие безинерционные преобразования параметров потока энергии) и др.

В настоящее время создают библиотеку математических моделей функционально законченных элементов, позволяющую построить общую модель технического объекта с учетом его структурного состава [17].

Как уже было отмечено ранее, блестящим завершением поиска наиболее удачного описания динамики механических систем с помощью дифференциальных уравнений явились труды Жозефа Луи Лагранжа (17361813 гг.), и особенно его «Аналитическая механика», опубликованная в

1788 г.

Особое значение при моделировании сложных технических систем приобрели уравнения Ж. Лагранжа второго рода. Их в настоящее время используют при построении моделей не только механических систем, но и объектов любой физической природы, если они рассматриваются как системы с сосредоточенными параметрами. При этом никаких ограничений на структуру и физические свойства объекта не накладываются.

Уравнения Ж. Лагранжа второго рода для системы с голономными связями имеют вид:

где Т - кинетическая энергия системы; qi – обобщенные координаты;

qi - обобщенная скорость;

Qi – обобщенная сила;

n – число степеней свободы системы.

Вывод этого уравнения не столь уже сложен, но выходит за рамки данного учебного пособия, тем более, что он приводится практически во всех учебниках и учебных пособиях по теоретической механике [27], [29], [30].

Если среди обобщенных сил имеют место потенциальные и диссипативные, то уравнение (5.22) может принять форму:

где П – потенциальная энергия системы; Ф – диссипативная функция Рэлея.

102

Обобщенная сила Qi, фигурирующая в этом уравнении, определяется с учетом работы источников всех внешних воздействий, а также некоторых внутренних источников, которые не могут быть отнесены к упругим и диссипативным элементам.

Очень часто уравнения Ж. Лагранжа используют при изучении колебаний машин и механизмов. Если при этом исследователя интересуют параметры свободных колебаний (т.е. Qi = 0), то уравнение принимают в виде (5.22), без учета диссипативной функции, а для изучения затухающих колебаний необходимо полное уравнение (5.23).

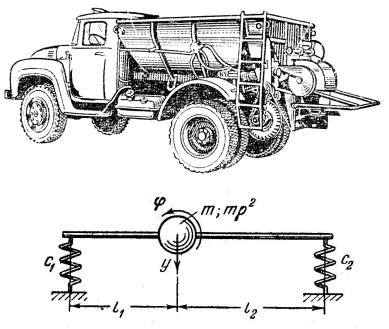
В качестве примера можно рассмотреть свободные колебания автомобильного разбрасывателя удобрений (рис. 5.22).

Обычно принимается, что переднюю и заднюю подвески можно представить в виде двух пружин; при этом раму и кузов машины вместе с другими, жестко связанными с ними телами схематически представляют в виде тела, обладающего конечным моментом инерции.

Если обозначить жесткости пружин как С1 и С2, через m и ρ – массу и радиус инерции тела, а в качестве обобщенных координат принять вертикальное перемещение центра тяжести у и угол поворота связанной с телом жесткой балки θ, тогда кинетическую и потенциальную энергии можно записать в виде:

Рис. 5.22. Схема к исследованию свободных колебаний машины для внесения удобрений

103

Производные, необходимые для подстановки в уравнение Ж.Лагранжа,

Если предположить, что параметры рассматриваемой системы удовлетворяют двум простым (и реально осуществимым) соотношениям:

тогда систему дифференциальных уравнений можно упростить:

т.е. линейные однородные уравнения второго порядка с постоянными коэффициентами.

Вид общего решения линейных дифференциальных уравнений, как известно, зависит от значений корней характеристических уравнений, которые в данном случае одинаковы:

2 k 2 0 .

Поскольку корни этого уравнения – чисто мнимые числа: 1 k i ,2 k i , то общим решением дифференциального уравнения для любой

переменной, допустим х, будет

x C1 coskt C2 sin kt ,

104

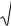
где в данном случае прописными буквами С1 и С2 обозначены постоянные интегрирования.

Для большего удобства анализа этого решения вводят обычно новые постоянные интегрирования А и α, предположив, что

C1 A sin , C2 A cos .

Это можно сделать, так как из этих соотношений постоянные А и α определяются через С1 и С2 с помощью формул:

Первое из колебаний представляет собой «подпрыгивание», не сопровождающееся поворотами рамы, а второе колебаний – «галопирование», при котором центр тяжести машины остается неподвижным, и происходят угловые колебания вокруг этой точки.

Постоянные А и α (или С1 и С2) определяются заданием начальных положений и скоростей движения точки. Коэффициенты А1 и А2 определяют амплитуду соответствующих колебаний, α1 и α2 – начальные фазы, а k – угловую частоту.

Вприведенном примере рассмотрен простейший случай колебаний – собственные колебания материальной точки (правая часть уравнения Лагранжа равная нулю). В случае, когда в правой части уравнения помещают обобщенную силу вязкого трения (например, в случае, когда хотят учесть влияние эластичных шин), то в результате решения приходят к затухающим колебаниям, а при воздействии внешних возмущающих сил (например, от воздействия неровностей поля) – к вынужденным колебаниям.

Вполне конкретные примеры использования уравнения Лагранжа второго рода есть в работах В.А. и Л.А. Гоберманов [13] (пятимассовая система плнетарного редуктора), В.А. Сысуева и др. [29] (движение рулона переменной массы в питателе-измельчителе раздатчика грубых кормов), В.П. Тарасика [17] (построение модели анализа динамических нагрузок в трансмиссии автомобиля при включении сцепления) и др. Примеры таких моделей применительно к исследованию почвообрабатывающих, посевных

ипосадочных, уборочных и других машин можно найти в работах А.Б. Лу-

рье [23], [24].

Одной из наиболее ранних работ в исследовании динамики рабочих органов сельскохозяйственных машин стала модель вынужденных колебаний сошника зерновой сеялки [23].

Расчетная схема модели представлена на рис. 5.23.

Вкачестве обобщенной координаты принят угол наклона поводка сошников к раме сеялки.

105

Под воздействием возмущающей силы со стороны поверхности почвы сошник совершает колебания около горизонтальной оси.

Силы, действующие на сошник, в общем случае зависят от его поло-

жения, скорости движения и времени:

Rx f1 , ,t , Rz f2 , ,t .

Рис. 5.23. Схема к выводу уравнения малых колебаний сошника

После проведения неполной линеаризации этих сил по формуле Тей-

лора

получено уравнение малых колебаний сошника в виде:

свойства сошника при движении его в почве и имеют размерность времени, масштабный коэффициент k (коэффициент усиления) имеет размерность 1/кг, f(t) – функция внешних возмущений.

Линеаризацию функции внешних возмущений осуществлять нельзя, так как поверхность поля не может быть представлена в виде непрерывной, гладкой, дифференцируемой функции.

Полный вывод этого уравнения с использованием различных методик приведен в работах [23], [24], [31].

Существенной особенностью моделей, основанных на использовании уравнения Ж. Лагранжа, является то, что оно приводит обычно к системе дифференциальных уравнений, содержащих столько уравнений, сколько независимых координат учитывает модель. Если потребуется описать движение машины в трехмерном пространстве, т.е. помимо курсового движения учесть еще возможность поперечного крена и поворота управляемых колес в горизонтальной плоскости, то система будет содержать шесть урав-

106

нений. В случае исследования более сложных механических систем, допустим «трактор+навесная машина» и «трактор+сцепка+с.-х. машина», число дифференциальных уравнений в системе может увеличиться до нескольких десятков.

Решение систем таких уравнений приводит к значительным трудностям, и в свое время потребовало создания так называемого операционного исчисления.

Основы операционного исчисления заложены английским физиком Оливером Хевисайдом (1850…1925 гг.), который при разработке вопросов теоретической электротехники ввел основные правила действий с операто-

ром dtd P и функциями этого оператора.

В этой системе действий дифференцирование функции х = х(t) рассматривается как умножение оператора Р на функцию Х = Х(Р) этого оператора.

т.е. операции дифференцирования он заменил на умножение оператора Р в соответствующей степени на некоторую функцию этого оператора Х(Р).

Интегрирование рассматривалось как деление функции Х(Р) на этот оператор Р:

Самое важное в этом методе состоит в том, что его использование позволило линейные дифференциальные уравнения свести к простым алгебраическим уравнениям относительно функции Х(Р). Установив для наиболее простых функций связь между f(x) и X(P), О. Хевисайд успешно использовал такой метод при решении инженерных задач. На замечание математиков о бездоказательности такого приема О.Хевисайд якобы возражал, что не должен отказываться от обеда, если не знает поварского дела. Так или иначе, его расчеты соответствовали действительности, и он свой метод использовал.

Только через год после смерти О. Хевисайда американский инженер Д. Карсон установил связь между операционным исчислением и интегральным преобразованием Лапласа. Соотношение между функцией-оригиналом f(t) и ее изображением F(P) по Лапласу, как известно, определяется интегральным уравнением:

L f t F P . Обратную зависимость между функциями изображения и

107

оригинала нашел английский математик Т. Бромвич в виде контурного интеграла:

для случая, когда f(t) изображается как F(P). Если необходима обратная зависимость, то F(P) f (t) , т.е. функция F(P) изображает функцию f(t).

После подстановки в уравнение (5.35) в качестве f(t) простых функ-

ций, допустим f(t)=1; f(t)=t; f (t) e t ; f(t) = sinωt; f(t)= cosωt, нетрудно

В современной справочной литературе приводятся многочисленные прямые и обратные соотношения между функциями-оригиналами и их изображениями. Особого внимания требует нахождение изображений производных.

Допустим, что известно изображение функции f(t)←F(P). Требуется найти изображение производной f (t)←?

В формулу интеграла Лапласа (5.26) подставим f (t) вместо f(t) и

Итак,

f (t) P F(P) f (0) ,

где f(0) – значение функции f(t) при начальных условиях. Совершенно аналогично можно вывести:

108

Эти уравнения представляют собой так называемую теорему изоб-

ражений, согласно которой операции дифференцирования оригинала соответствует умножение изображения на Р.

От уравнений, используемых О. Хевисайдом, эти соотношения отличаются только учетом начальных значений функций и их производных.

Изображение интеграла. Интегрирование оригинала от нуля до переменной точки t соответствует в пространстве изображений деление изображения на Р:

Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу найти изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» [32] или в соответствующих разделах математической литературы [33].

Решение дифференциальных уравнений операционным методом можно наглядно изобразить в виде схемы:

Схема

Пусть, например, требуется найти решение линейного дифференциального уравнения с постоянными коэффициентами:

К такому виду, в частности, приводится в теории колебаний [34] общее дифференциальное уравнение вынужденных колебаний системы с учетом сил сопротивления. Примером такой модели при исследовании движения рабочих органов сельскохозяйственных машин является уравнение малых колебаний сошника сеялки [24], [31]:

Т12 Т2 кf (t) .

При исследованиях динамики механических систем их модели часто представляют в виде, как говорят «черного ящика», преобразующего определенным образом входные воздействия f(xi) c выходными, искомыми параметрами уi (рис. 5.24).

109

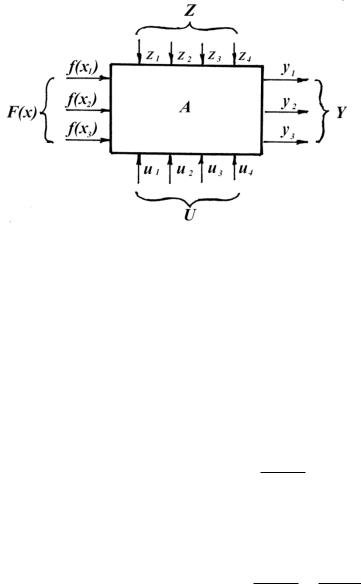
Помимо входных воздействий с вектором F(x) на работу системы могут оказывать влияние вектор состояния элементов Z и вектор U управляющих воздействий со стороны оператора. С помощью такой схемы достигается предельное абстрагирование модели от реального объекта и сосредоточение внимания на связях воздействий и результатов работы.

Свойства самой системы А могут быть описаны, как об этом было отмечено ранее, решением системы дифференциальных уравнений, связывающих входные воздействия векторов F(x), Z и U на выходные параметры Y, что, вообще говоря, представляет собой сложную задачу.

Рис. 5.24. Схема функционирования динамической системы

Гораздо проще связь входных и выходных параметров может быть установлена, если дифференциальные уравнения, связывающие эти параметры, представить в преобразованиях Лапласа.

В общем виде такая замена может быть представлена как

L1(P) Y (P) L2 (P) X (P) ,

где L1(P), L2(P) – преобразования Лапласа выходных и входных воздействий.

В этих терминах связь между входом и выходом, определяющая свойство системы А, правда в операторной форме, может быть установлена легко:

Y (P) L2 (P) X (P) .

L1(P)

Отношение преобразований Лапласа выходного параметра к входному называется передаточной функцией, которую чаще всего обозначают как W(P), т.е.

W (P) L2 (P) Y (P) . L1(P) X (P)

Таким образом, передаточная функция определяет операторную про-

водимость объекта (системы).

Если обратиться к примеру с колебаниями сошников, то в терминах «входа» и «выхода» уравнение преобразуется к виду:

Т12 у Т2 у у kх ,

110