892

В.П. Горячкин предложил учесть лишь главное обстоятельство, известное из курса физики: чем тяжелее тело, тем больше сила трения.

P1 = f G,

где f – коэффициент трения; G – сила веса.

Но поскольку сила Р1 затрачивается еще и на перекатывание колеса, то под коэффициентом f стали понимать не коэффициент трения, а коэф-

фициент перекатывания плуга.

Вторую составляющую Р2 В.П. Горячкин выразил по аналогии с разрушением образцов в курсе «Сопротивление материалов», как

Р2 = k а b,

где k – коэффициент крошения почвы.

Третья составляющая, Р3 найдена с использованием простых закономерностей механики.

Кинетическая энергия отбрасываемого пласта равна:

W mV12 ,

2

где m – масса отбрасываемой почвы; V1 – скорость отбрасывания пласта.

Скорость отбрасывания V1 не равна скорости движения пахотного агрегата V, но пропорциональна ей, т.е.

V1 = ε1 V.

Масса почвы, отбрасываемая в единицу времени равна: m = ρ a b V,

где ρ – плотность почвы. В таком случае

W 1 2 abV 3 , или W = ε a b V3, если обозначить ε = ρ ε12/2,

2

где ε – так называемый скоростной коэффициент.

Но кинетическая энергия W может быть представлена как величина работы в единицу времени, т.е.

W = A = P3 l1 = P3 V,

где l1 – путь, пройденный плугом в единицу времени.

Если поставить в эту формулу значения W и выразить величину Р3,

Это соотношение представляет собой так называемую рациональную формулу В.П. Горячкина. В последующем эта формула была значительно усложнена с учетом многих факторов, таких, например, как изменение удельного сопротивления почвы, влияние формы лемешно-отвальной поверхности, случайного характера всех факторов, но это уже другие, более точные, но менее очевидные модели.

В ряде случаев математические модели могут быть представлены в

91

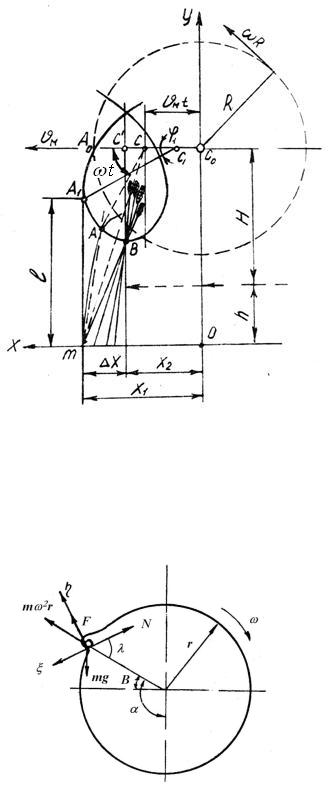
виде систем алгебраических уравнений. Примером таких моделей могут быть траектории движения рабочих органов (допустим, почвенных фрез, мотовила), записанные в параметрическом виде:

Рис. 5.16. Схема работы планки мотовила

Часто такими моделями пользуются при описании условий статической устойчивости, например, для определения фазы поворота триерного

где η и – подвижные оси координат, направленные по касательной к поверхности ячейки и перпендикулярно ей.

Рис. 5.17. Условия устойчивого положения семян в ячейках

92

5.5.2. Математические модели в виде дифференциальных уравнений,

составленных с использованием принципа Даламбера

Математические модели, представленные обыкновенными дифференциальными уравнениями, нашли широкое применение для описания взаимодействия рабочих органов сельскохозяйственных машин с обрабатываемой средой, для анализа движения динамических систем, для различного рода возмущений, воздействующих на сельскохозяйственную технику, при исследовании различных физических явлений – гидравлических, электрических, электромагнитных и т.д.

Широкое использование обыкновенных дифференциальных уравнений объясняется рядом причин. Во-первых, теория дифференциальных уравнений достаточно хорошо разработана; во-вторых, модели, составленные из дифференциальных уравнений, оказались настолько удачными, что нашли применение не только в задачах механики, но и для описания различных процессов в биологии, агрономии, что очень значимо именно для земледельческой механики, имеющей непосредственную связь с живой природой.

Существует много методов составления моделей на основе дифференциальных уравнений. При исследовании сельскохозяйственной техники наиболее распространенным является использование принципа Ж. Даламбера, уравнений Ж. Лагранжа и П. Аппеля.

Принцип Ж. Даламбера состоит в том, что сила инерции движущейся массы (по модулю равная произведению массы на ее ускорение) уравновешивается суммой проекций всех действующих на эту частицу сил (или про-

екций сил) в направлении возможного перемещения, т.е. mx Px .

В качестве примера может быть представлена задача описания движения материала по шероховатой поверхности, очень основательно изученная в свое время проф. П.М. Василенко [26].

При исследовании работы центробежных распределительных дисков машин для внесения удобрений необходимо определять скорость схода удобрений с диска, время пребывания их на диске в зависимости от размеров и режима работы распределительного аппарата.

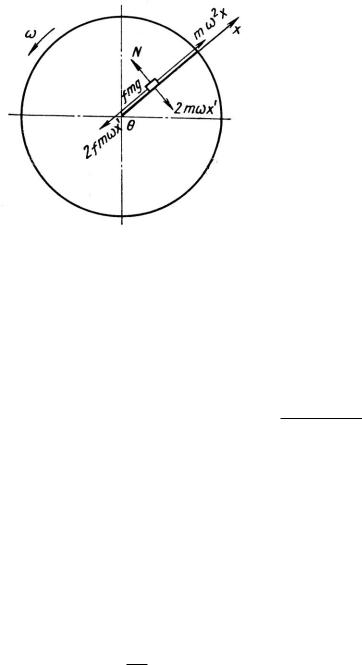
Если рассмотреть движение удобрений в самом простом случае по радиальным лопастям плоского диска (рис.5.18), то силами, действующими на удобрения, являются центробежная сила mω2x, сила Кориолиса, действующая на лопасть 2m x , силы трения (удобрений по лопасти 2 fm x и

по поверхности самого горизонтального диска fmg).

Предполагается, что коэффициент трения удобрений f по лопасти и диску одинаков.

Дифференциальное уравнение движения удобрений вдоль лопасти имеет вид:

поскольку проекция силы Кариолиса на лопасть окажется равной нулю.

93

После сокращения правой и левой частей на m и переноса неизвестных в левую часть соотношение (5.20) сводится к неоднородному линейному дифференциальному уравнению:

x 2 f x 2 x fg .

Рис. 5.18. Схема сил, действующих на частицу, движущуюся по радиальным лопастям плоского диска

Известно, что решение такого уравнения включает в себя общий и частный х1 интегралы:

х = u + x1.

Общий интеграл находят в зависимости от вида корней характеристического уравнения:

2 2 f 2 0 .

Корни этого квадратного уравнения оказываются действительными числами и отличаются друг от друга:

1,2 f 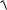f 2 2 2 .

В этом случае общее решение дифференциального уравнения имеет

вид:

u c1е 1t c2е 2t ,

где с1 и с2 – постоянные интегрирования.

В случае, когда в правой части дифференциального уравнения находится постоянная величина, то частный интеграл повторяет ее вид, т.е. тоже является постоянной величиной, х1 = А.

Если А подставить в дифференциальное уравнение, то окажется, что

0 + 2f ω0 - ω2A = -fg.

Откуда А fg .

Таким образом

где r0 – место подачи удобрений на диск.

94

Чтобы воспользоваться вторым начальным условием, необходимо иметь уравнение, описывающее скорость относительного движения удобрений вдоль лопасти. Для получения такого уравнения можно продифференцировать соотношение, определяющее перемещение (5.13):

После подстановки этих значений в (5.13) и (5.14) определяются уравнения, описывающие перемещения и скорости удобрений в произвольный момент времени:

В момент схода частиц с диска х = R (где R – радиус диска), т.е.

Решив это уравнение относительно t, находят время пребывания удобрений на диске, а после подстановки этого времени в уравнение (5.16) – радиальную скорость частиц при сходе с дисков. Начальная скорость схода частиц с дисков при радиальных лопастях будет равна:

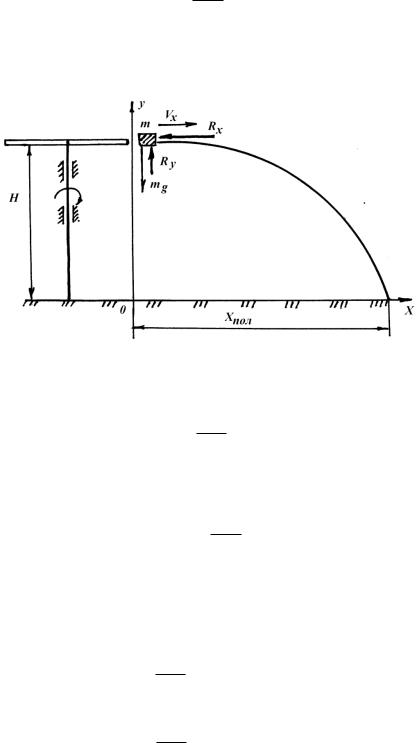
Движение удобрений после схода с распределительных дисков также может быть описано дифференциальным уравнением, составленным с использованием принципа Ж. Даламбера (рис. 5.19):

mx Rx ,

где Rx – сила сопротивления воздуха.

95

В диапазоне возможных скоростей полета сила Rx может быть найде-

на по формуле И. Ньютона:

Rx k F x 2 , g

где k – коэффициент, зависящий от шероховатости тела; ρ = γ/g – плотность среды;

F – площадь Миделева сечения.

Рис. 5.19. Движение удобрений после схода с центробежного диска

После подстановки Rx в дифференциальное уравнение получаем:

x k F x 2 . mg

Дробь, стоящую перед (x)2 , в правой части называют коэффициен-

том парусности:

Кп k F . mg

С учетом этого уравнение приобретет вид:

x Kп x2 .

Решение данного уравнения может быть осуществлено методом понижения порядка:

dVdtx KnVx2 ;

или после разделения переменных:

dVx Kndx , Vx

так как Vxdt = dx.

Интегрируя правую и левую части, получаем: ln Vx ln e kn x ln c1 ,

где с1 – постоянная интегрирования.

96

После потенцирования получится, что

Vx c1 e kn x .

Постоянную с1 можно найти из начальных условий, поскольку при

х= 0, Vx = Vнач, тогда

Vx Vнач e Kn x .

Для нахождения дальности полета требуется еще раз произвести понижение порядка, т.е.

где с2 – очередная постоянная интегрирования, которую можно найти из начальных условий – при t = 0 перемещение х = 0:

Kn x ln(Vнач t Kn 1) .

При определении времени падения частиц с высоты Н до поверхности почвы сопротивление среды обычно не учитывают, так как скорость падения относительно мала.

Попытки найти это время с учетом сопротивления среды показали, что уточнение оказывается незначительным.

С учетом этого дальность полета частиц может быть определена:

Уравнения (5.15), (5.16) и (5.18), представляющие собой основные технологические характеристики процесса, введены в компьютерную программу, позволяющую провести вычислительный эксперимент при анализе зависимости дальности полета, а, следовательно, и ширины захвата машины от таких параметров, как частота вращения дисков, размер дисков, места подачи удобрений на диск. Поскольку исходная модель, введенная в компьютер, была не-

97

сколько усложнена с учетом возможностей изменения углов наклонов лопастей и анализа конусных дисков, то дополнительно появилась возможность провести вычислительный эксперимент и для этих параметров. Анализ результатов вычислительного эксперимента показывает, в частности, что для обеспечения большой ширины захвата необходимо использовать конусный диск с углом бросания 10…15 и вносить гранулированные удобрения.

5.5.3. Математические модели, основанные на использовании уравнений Ж.Лагранжа

Уравнения Ж. Лагранжа, основанные на общем уравнении динамики механических систем, представляют собой наиболее обоснованный подход к образованию моделей.

Идея, лежащая в основе общего уравнения, состоит из использования принципа Ж. Даламбера, позволяющего записывать динамические уравнения в виде уравнений равновесия с добавлением к действующим активным силам сил инерции.

Но если такая система сил уравновешена, то к ней применим принцип возможных перемещений Лагранжа.

Последовательное применение этих принципов к движущейся механической системе позволяет сформулировать принцип ДаламбераЛагранжа: если к движущейся механической системе, на которую наложены голономные связи, условно приложить силы инерции всех ее точек, то в каждый момент времени сумма элементарных работ активных сил и сил

miqi – сила инерции точки Мi массой mi в направлении qi;

i = (1…n) – номер точки М в динамической системе.

Если мысленно зафиксировать время t, и дать системе виртуальное перемещение δri (i = 1…n), перемножить на него каждое слагаемое уравнения (5.19) и сложить результат, то

Под связями механической системы понимают ограничения, стесняющие движение тел. Обычно это шарнирные опоры, опорные поверхности, жесткие или упругие заделки стержней и балок и т.п.

В общем случае уравнение связи, налагаемой на систему точек, запи-

В зависимости от вида данной функции связи делятся так:

-геометрические и дифференциальные;

-стационарные и нестационарные;

-удерживающие и неудерживающие.

98

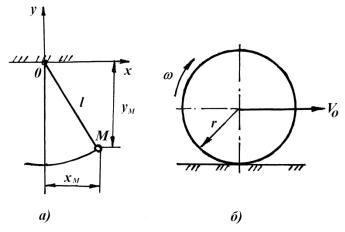
К геометрическим относятся связи, в уравнения которых входят только координаты точек системы, и, может быть, время. Например, в случае математического маятника с подвесом в начале координат (рис. 5.20а) уравнение связи имеет вид:

хМ2 уМ2 l2 или

xM2 yM2 l2 0 .

Рис. 5.20. Виды связей динамических систем: а – геометрические, б – дифференциальные

Дифференциальными называются связи, уравнения которых, кроме координат точек системы, содержат и первые производные от этих координат по времени и, может быть, время. Примером дифференциальной связи может быть ограничение, накладываемое на колесо, катящееся без скольжения по неподвижной поверхности (рис. 5.20б).

В этом случае скорость центра колеса и его угловая скорость связаны между собой:

V0 = ω r, или V0 – ω r = 0 .

К голономным относятся все геометрические связи, а также те из дифференциальных, которые путем интегрирования могут быть сведены к геометрическим.

Рассмотренная выше дифференциальная связь, наложенная на колесо, является голономной, так как ее уравнение можно проинтегрировать и свести к геометрической.

Действительно, V0 = ω r, т.е. dx0 = r dθ,

Виртуальные перемещения – это воображаемые бесконечно малые перемещения системы из одного ее положения в другое, допускае-

мое связями в тот же момент времени без освобождения от связей.

~

Виртуальным перемещением r соответствуют изменения координат и обозначаются δх, δу, δz, в отличие от обозначения дифференциалов dx, dy и dz.

99

Дифференциалы представляют собой тоже бесконечно малые изменения координат, но за определенный, пусть малый промежуток времени dt, под действием приложенных к системе сил.

Операции дифференцирования и варьирования являются независимыми одна за другой, поэтому имеет место равенство:

δ(df)=d(δf),

где f – какая-либо непрерывная функция координат, скоростей и вре-

мени.

Изменения функции f от вариаций координат, т.е. δf(x,y,z,t) называется вариацией функции f.

Если сумма элементарных работ на всех виртуальных перемещениях системы равна нулю, т.е. если

n

Ri ri 0 ,

i 1

или то же самое в проекциях на оси координат

n Rix xi Riy yi Riz zi 0 ,

i 1

то связи называют идеальными.

Идеальными связями будут, например, абсолютно гладкие (без трения) опорные поверхности, нерастяжимые, несжимаемые и несгибаемые стержни и т.п., входящие в состав основных допущений в задачах, представляющих собой первое приближение к действительности.

Независимые или обобщенные координаты. Если система состоит из

N точек, то ее пространственное положение может быть описано 3N координатами (x,y,z). При наличии S голономных связей, ограничивающих перемещения, положения точек описывают через остальные, независимые ко-

ординаты.

Часто вместо обычных, декартовых координат выбирают другие, связанные с ними величины, иногда другой природы и размерности.

Эти независимые величины называют обобщенными координатами, например q1,q2,q3,….,qn, где n = 3N - S, причем n называют числом степеней свободы.

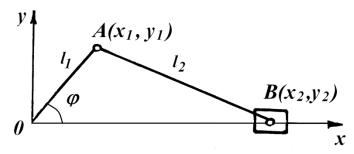
Пусть, например, исследуется работа кривошипно-шатунного механизма (рис. 5.21)

Рис. 5.21. Схема к выбору обобщенной

координаты кривошипно-шатунного механизма

Положение точек О, А и В определяется шестью координатами: х0у0; х1у1; х2у2.

100