
892
.pdf
формируют случайные числа с равномерным распределением, а затем, с помощью тех или иных преобразований, получают величины с заданным законом распределения. Практически все современные ЭВМ имеют встроенные подпрограммы вычислений случайных чисел с равномерным распределением в интервале (0,1).
Известно, что при равномерном распределении в интервале (0,1) непрерывная случайная величина имеет плотность распределения:
|
|
1 |
при 0 х 1 |
|
f |
|
|
|
. |
|
(x) |
при x 0 |
||
|
0 |
и x 1 |
||
|
|
|
|
|
Математическое ожидание равно m 1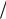 2 .
2 .
Дисперсия D 1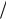 12 , а 1/(2
12 , а 1/(2
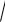 3) .
3) .
Равномерно распределенные числа Ri могут быть преобразованы в случайные числа Si с заданным законом распределения посредством решения интегрального уравнения:
Si |
|
f (x)dx Ri . |
(5.104) |
Для показательного распределения (которое лежит в основе распределения семян в рядке при пунктирном посеве)
f (x) e x .
Тогда в силу соотношения (5.104)
Si
e xdx Ri ,
0
или после вычислений интеграла
1 е i Si Ri .
Решая это уравнение относительно Si можно получить:
S |
|
|
1 |
ln(1 R ) . |
(5.105) |
i |
|
||||
|
|
|
i |
|
|
|
|
|
|
|
Иными словами, чтобы получить случайные числа с экспоненциальным распределением, необходимо взять логарифм от (1 - Ri), а поскольку эта разность представляет собой также равномерно распределенную величину, то и lnRi будет распределен по показательному закону.
Суммируя (k + 1) отрезок Si, можно получить числа с гаммараспределением, которые будут характеризовать размещение семян в рядке:
k 1 |
|
Li Si . |
(5.106) |
i 1
Моделирование процесса всхожести отдельных семян представляется возможным осуществить сравнением конкретного случайного числа Ri с принятой величиной всхожести Р. Если Ri Р, то семя можно считать всхожим, а если Ri > P – семя можно отнести к невзошедшему.
В случае, когда такая проверка заканчивается положительно (семя всхожее), формирование интервала заканчивают, а если нет, то к сформи-
151

рованному уже интервалу добавляют (k+1) отрезок с показательным распределением (или, что то же самое - следующий отрезок Li), и вновь следует проверка на всхожесть.
Таким образом может быть сформирован массив чисел, характеризующих размещение растений в рядке.
Внекоторых случаях преобразование случайных чисел Ri по уравнению (5.104) оказывается неэффективным. Прежде всего это случается, когда интегральное уравнение (5.104) не может быть решено точно. В частности, рассмотренный метод является неприемлемым для получения последовательности чисел, имеющих нормальное распределение. В этом случае используют приемы преобразования случайных чисел, основанные на моделировании условий, при которых оказываются справедливыми предельные теоремы теории вероятностей.
Всилу центральной предельной теоремы сумма большого числа случайных слагаемых (при выполнении весьма общих условий) имеет асимптотически нормальное распределение. Иными словами, некоторая нормаль-
но распределенная случайная величина (например, длина букета или выреза) может быть представлена как сумма независимых одинаково распределенных величин:
1 2 3... п . |
(5.107) |
Математическое ожидание и средне-квадратическое отклонение такой суммы равны:
ас = а*n; c 
 n ,
n ,
где а*, * - числовые характеристики i.
Для равномерно-распределенных величин а 1/ 2 ; 1/(2
 3) ,
3) ,
тогда ас n / 2 и c (1/ 2
 n / 3) .
n / 3) .
Таким образом, чтобы получить случайные числа с нормальным распределением, необходимо на ЭВМ вызвать n последовательных случайных чисел Ri с равномерным распределением и просуммировать их:
|
|
|
|
|
n |
|
|
|||
|
R Ri . |
(5.108) |
||||||||
|
|
|
|
i 1 |
|
|
||||
Чтобы пронормировать распределение этих чисел, каждое из чисел R |
||||||||||
нужно преобразовать: |
~ |
|
|
|
|
|
|
|
|
|
|
(R ac ) / c . |
|||||||||
|
R |
|||||||||
Учитывая значения ас и c, можно записать: |
||||||||||
|
~ |
|
2 |
|
3 |
(R |
n |
|||
|
R |
|
|
|
|
|
) . |
|||
|
|
|
|
|
|
2 |
||||
|
|
|
n |
|||||||
Для получения чисел Rз, образующих последовательность с другими, заданными параметрами mз и з (например mбукета, букета или mвыреза и выреза)
необходимо провести еще одно преобразование. |
|
|||
Поскольку |
~ |
|
~ |
|
|
(Rз mз ) / з , |
mз . |
||
|
R |
то Rз R 3 |
||
152
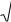
~
После подстановки значения R можно получить случайные числа с нормальным распределением и заданными параметрами:
|
|
|
n |
|
|
|
|
Rз |
A Ri |
B , |
(5.109) |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
где А 2 3 3/ n, |
В m3 |
Аn / 2. |
|
|
|
По этому уравнению можно сформировать массив чисел, характеризующих вырезанные и невырезанные участки рядка при «слепом» и автоматическом прореживании.
Подсчет числа растений, оставшихся в букетах, и определение характеристик их размещения могут быть осуществлены обычными методами математической статистики.
Программа Пунктир (Punktir), разработанная на кафедре сельскохозяйственных машин Пермской ГСХА, предусматривает формирование 5000 расстояний между семенами, моделирование чередования всхожих и невсхожих семян, моделирование участков «вырез», «невырез» по схемам «слепого» и автоматического прореживания и определение результатов прореживания (числовые характеристики, ряды распределения, многоугольники распределения).
На основе проведенных расчетов можно обоснованно выбрать схему обработки и назначить параметры технологического процесса прореживания.
Пример определения результатов имитационного моделирования формирования густоты насаждений при пунктирном посеве
ипрореживании растений различными методами
Вкомпьютер введены следующие исходные данные:
Вариант «слепого» прореживания
Всхожесть семян, % - 60.
Среднее расстояние между семенами, см – 4. Коэффициент вариации, % - 60; Величина междурядья, см – 45;
Вы используете автоматический прореживатель ПСА 2,7(Y,N)-n; Средняя длина букета, см – 6.
Среднеквадратическое отклонение длины букета, см – 1. Средняя величина выреза, см - 6.
Среднее квадратическое отклонение выреза, см – 1.
|
|
|
|
Таблица 5.14 |
||
Результаты расчета при «слепом» прореживании |
|
|||||
|
|
|
|
|
|
|
|
|
Среднее |
Число |
Длина |
Коэф- |
|
|
Среднее |
фици- |
||||
|
квадратиче- |
семян и |
модели- |
|||
Характеристика |
значе- |
ент ва- |
||||
ское откло- |
расте- |
руемого |
||||
|
ние, mср |
риации, |
||||
|
нение, см |
ний |
рядка, м |
|||
|
|
% |
||||
|
|
|
|
|
||
По посеву семян |
4,023 |
2,313 |
3500 |
140,82 |
57,5 |
|
По всходам |
6,890 |
5,254 |
2043 |
140,82 |
76,28 |
|
153
После прореживания |
13,692 |
11,211 |
1028 |
140,76 |
81,88 |
По площади питания |
|
|
|
|
|
растений, см2 |
615,866 |
351,197 |
- |
- |
57,02 |
В процессе расчетов сформированы следующие ряды распределения: расстояния между семенами
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
0 |
1,82 |
3,64 |
5,46 |
|
7,28 |
9,09 |
|
10,91 |
12,73 |
|
14,55 |
|
|
16,37 |
|
18,19 |
||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
556 |
|
|
1227 |
|
|
939 |
|
|
450 |
|
210 |
|
|
79 |
|
|
23 |
|
9 |
|
|
6 |
|
1 |
||||||
|
|
|
|
|
|
|
|
|
Расстояния между всходами |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
0 |
5,52 |
11,04 |
16,57 |
|
22,09 |
27,61 |
33,13 |
38,66 |
44,18 |
|
49,30 |
55,22 |
||||||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
1031 |
|
667 |
|
|
233 |
|
|
|
73 |
|
|
24 |
|
|
11 |
|
|
2 |
|
1 |
|
|
0 |
|
1 |
|||||
|
Расстояния между растениями после прореживания |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
0 |
8,18 |
16,37 |
24,55 |
32,74 |
40,92 |
49,10 |
57,29 |
65,47 |
73,66 |
81,84 |
||||||||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
329 |
|
|
411 |
|
|
136 |
|
|
|
79 |
|
|
45 |
|
|
13 |
|
|
7 |
|
7 |
|
|
0 |
|
1 |
||||
|
|
Площади питания растений после прореживания |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
234,16 468,32 702,48 936,63 1170,79 1404,95 1639,11 1873,27 2107,43 |
||||||||||||||||||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
67 |
|
322 |
|
285 |
185 |
|
100 |
|
38 |
|
|
17 |
|
6 |
|
|
5 |
|
|
2 |
||||||||||
Вариант селективного прореживания
Всхожесть семян, % - 60.
Среднее расстояние между семенами, см – 4,0. Коэффициент вариации, % - 60.
Величина междурядья, см – 45.
Вы используете автоматический прореживатель ПСА-2,7 (Y,N)-Y. Длина букета, см – 6.
Длина переднего ножа, см – 6. Длина заднего ножа, см – 6.
154
Шаг прореживания, см – 12.
Таблица 5.15
Результаты расчета при автоматическом прореживании
Числовые ха- |
Среднее |
Среднее |
Коэффици- |
Длина моде- |
Число |
рактеристики |
значе- |
квадратиче- |
ент вариа- |
лируемого |
семян и |
|
ние, mср |
ское отклоне- |
ции, % |
рядка, м |
расте- |
|
|
ние, см |
|
|
ний |
По посеву се- |
|
|
|
|
|
мян |
3,964 |
2,284 |
57,62 |
3500 |
138,74 |
По всходам |
6,719 |
5,124 |
76,26 |
2065 |
138,74 |
После проре- |
|
|
|
|
|
живания |
12,084 |
6,944 |
57,46 |
1148 |
138,74 |
По площади |
|
|
|
|
|
питания рас- |
|
|
|
|
|
тений, см2 |
543,916 |
216,878 |
39,87 |
- |
- |
В процессе расчетов сформированы следующие ряды распределения: расстояния между семенами
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
1,66 |
3,32 |
|
4,99 |
|
6,65 |
|
8,31 |
9,97 |
|
11,63 |
13,29 |
|
14,96 |
|
||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
474 |
|
1109 |
|
984 |
|
504 |
|
|
243 |
|
115 |
|
|
47 |
|
|
17 |
|
|
|
2 |
|
5 |
|||||
Расстояния между всходами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
3,90 |
|
7,81 |
|
11,71 |
|
15,62 |
19,52 |
23,43 |
27,33 |
31,24 |
|
35,14 |
||||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
719 |
|
721 |
|
332 |
|
155 |
|
|
|
71 |
|
|
41 |
|
|
14 |
|
|
8 |
|
|
|
2 |
|
2 |
|||
Расстояния между растениями после прореживания |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
4,45 |
8,89 |
13,34 |
17,79 |
22,23 |
26,18 |
31,13 |
35,58 |
40,02 |
||||||||||||||||||||
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шт |
262 |
|
24 |
|
327 |
|
352 |
|
|
117 |
|
|
39 |
|
|
15 |
|
|
9 |
|
|
|
2 |
|
1 |
||||
Площади питания растений после прореживания |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
классов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
131,82 |
263,63 |
|
395,45 |
527,26 |
659,08 |
790,89 922,71 |
1054,52 |
1186,34 |
||||||||||||||||||||
155

Частота, |
|
|
|
|
|
|
|
|
|
|
шт |
24 |
59 |
263 |
187 |
256 |
213 |
101 |
31 |
9 |
4 |
Сравнение результатов «слепого» селективного прореживания обнаруживает, что даже при одинаковых схемах, обеспечивающих удаление половины растений, равномерность оставшихся растений после ПСА-2,7 гораздо выше (коэффициент вариации 54,46% против 81,88%).
Использование метода вычислительного эксперимента, использующего имитационные модели формирования густоты насаждений, может выявить влияние того или иного параметра технологического процесса на равномерность конечного распределения растений.
В качестве примера определенно влияние шага прореживания на характеристики распределения растений.
Исходная характеристика посева семян принята одинаковой, т.е. шаг размещения семян а = 4см с коэффициентами вариации V = 60% (характерный для современных сеялок), всхожесть семян Р = 60%, число моделируемых расстояний между семенами n = 3500.
Таблица 5.16
Числовые характеристики распределения растений после прореживания по различным схемам
|
Среднее |
|
|
|
Коэффи- |
|
|
расстоя- |
|
|
Число |
||
|
|
|
циент ва- |
|||
Схема |
ние |
Среднеквадра- |
Длина мо- |
остав- |
||
риации |
||||||
прорежи- |
между |
тическое откло- |
делируемо- |
шихся |
||
распреде- |
||||||
вания, см |
расте- |
нение, см |
го рядка, м |
расте- |
||
ления |
||||||
|
ниями, |
|
|
ний, шт |
||
|
|
|
растений |
|||
|
см |
|
|
|
||
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
|
4х4 |
13,630 |
10,770 |
139,43 |
1023 |
79,00 |
|
6х6 |
13,692 |
11,211 |
140,76 |
1028 |
80,30 |
|
8х8 |
13,118 |
11,059 |
137,34 |
1047 |
84,30 |
|
10х10 |
13,399 |
11,486 |
140,28 |
1047 |
85,72 |
|
12х12 |
13,278 |
11,428 |
140,22 |
1056 |
86,06 |
|
15х15 |
13,300 |
11,805 |
137,92 |
1037 |
88,76 |
|
20х20 |
13,361 |
13,426 |
140,29 |
1050 |
100,49 |
|
25х25 |
13,476 |
14,030 |
141,90 |
1053 |
104,11 |
|
30х30 |
13,862 |
15,426 |
140,70 |
1015 |
111,28 |
|
35х35 |
13,403 |
16,228 |
141,14 |
1053 |
121,08 |
|
40х40 |
14,060 |
18,370 |
140,88 |
1002 |
130,65 |
|
45х45 |
13,465 |
18,284 |
140,17 |
1041 |
135,79 |
Результаты расчета свидетельствуют, что увеличение шага прореживания неизбежно ведет к росту коэффициента вариации, т.е. к существенному снижению равномерности распределения растений.
156
5.5.9. Модели, основанные на использовании теории случайных функций
Работа сельскохозяйственных агрегатов протекает, как правило, в условиях изменяющихся внешних воздействий, обусловленных многочисленными и разнообразными факторами (неровности поверхности поля, непостоянство физико-механических свойств почвы и т.д.) Случайный характер факторов, воздействующих на сельскохозяйственные машины, является основной особенностью условий их функционирования.
Все случайные возмущения, действующие на сельскохозяйственные агрегаты и их рабочие органы, непрерывно изменяются в зависимости от пути, пройденного машиной, или времени и являются, таким образом, случайными функциями.
Случайной называется такая функция, которая в результате опыта может принять тот или иной вид, причем неизвестно заранее – какой именно.
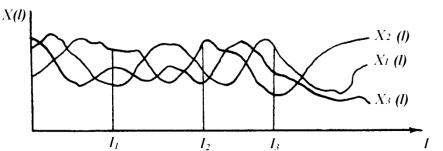
Аналогично тому, как случайную величину описывает совокупность возможных значений, с учетом частоты появления этих значений случайную функцию можно представить в виде семейства или ансамбля возможных реализаций (рис. 5.51).
Рис. 5.51. Ансамбль реализации случайной функции
Отметим, что в каждом сечении (l1; l2; l3 и т.д.) мы имеем обычные случайные величины. Случайная функция может иметь различный аргумент (длина рядка, путь, время, координаты положения и т.д.).
Если аргументом случайной функции является время, то такую функцию называют случайным процессом. Часто встречаются такие случайные процессы, которые имеют вид непрерывных случайных колебаний около некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени. Такие случайные процессы называют стационарными. (Например, профиль поверхности поля на ровном участке, колебания сошника около среднего положения, масса валка хлебной массы и т.д.). Вообще говоря, профиль поверхности поля является функцией пути, но поскольку воздействие микронеровностей на рабочие органы и агрегат в целом зависит от скорости движения агрегата, то при каждой определенной скорости движения машины изменение профиля поля считают случайным процессом. При обработке наблюдений над стационарным случайным процессом часто возникает вопрос: существенно ли необходимо располагать несколь-
157
кими реализациями?
Поскольку стационарный процесс протекает однородно во времени, то можно предположить, что одна единственная реализация, но большой длительности, может служить достаточным опытным материалом для получения характеристик случайной функции.
Стационарные процессы, у которых любые характеристики, полученные по ансамблю реализаций, совпадают со средним по аргументу (т.е., могут быть представлены в виде одной достаточно продолжительной реализации), называют эргодическими. В практике использования статистической динамики с.-х. агрегатов обычно принимают предпосылку об эргодичности случайных процессов.
Характеристики случайных функций
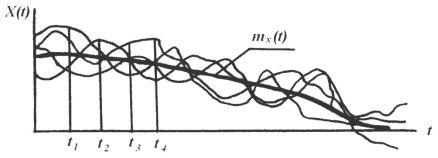
Пусть имеется случайный процесс X(t) (рис. 5.52). Для определения математического ожидания (среднего значения) случайной функции находят среднее значение каждого сечения (t1, t2, t3) и соединяют точки между собой:
mx (t) M X (t) .
Рис. 5.52. Функция математического ожидания
Математическим ожиданием случайной функции X(t) называется неслучайная функция mx(t), которая при каждом сечении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
Аналогичным образом определяется дисперсия случайной функции:
Dx (t) D X (t) .
Дисперсией случайной функции X(t) называется неслучайная функция Dх(t), значение которой для каждого t равно дисперсии соответствующего сечения случайной функции. Дисперсия случайной функции характеризует возможный разброс отдельных реализаций относительно среднего значения.
Для стационарного случайного процесса математическое ожидание и
дисперсия являются конкретными числами mx и Dх, а не функциями. |
||||||||
|
1 |
|
|
X (ti ) mx |
2 |
|
2 |
|
mx |
x(ti ) ; Dx |
|
|
x(ti ) |
|
; |
||
n |
|
n |
n |
|
||||
|
|
|
|
|
|
|||
Если для случайных величин среднее значение и дисперсия являются исчерпывающими числовыми характеристиками, то для случайных функ-
158
ций это не так.
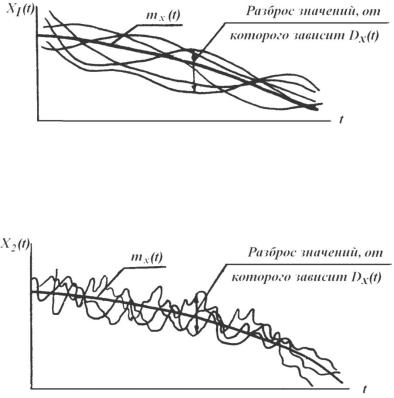
Рассмотрим две случайные функции, у которых приблизительно одинаково mx(t) и Dх(t) (рис. 5.53, 5.54).
Рис 5.53. Случайная функция с плавно протекающим процессом
Если функция Х1(t) имеет плавный, спокойный характер изменения ее значений, то Х2(t) – резко переменный.
Рис. 5.54. Случайная функция с резко переменным процессом
Таким образом, внутренняя структура процесса не улавливается ни значением mx(t), ни Dх(t). Для выявления структуры процесса вводится специальная характеристика, которая называется корреляционной функцией. Корреляционная функция характеризует связь между значениями случайной функции, относящимися к различным t (или при различном расстоянии между сечениями η):
R |
M |
|
|
|
|
, |
(5.110) |
|
Х t |
X t |
|
||||
x |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
т.е. корреляционной функцией случайной функции называется неслучайная функция двух аргументов Rx(ti, ti+η), которая при каждой паре значений ti и ti+η равна корреляционному моменту соответствующих сечений случайной функции. Для эргодического стационарного случайного процесса корреляционная функция определяется средней величиной произведения центрированных ординат, отстоящих друг от друга на расстоянии η. Заметим, что
X (t) и X (t1 ) – это центрированные значения случайных функций, т.е.
,
X (ti ) X ti mx (t) .
В случае, когда ti = ti + η, т.е. η = 0, то Rx(η) = Dx(t), так что необходимость в использовании отдельной характеристики – дисперсии случайной функции – отпадает.
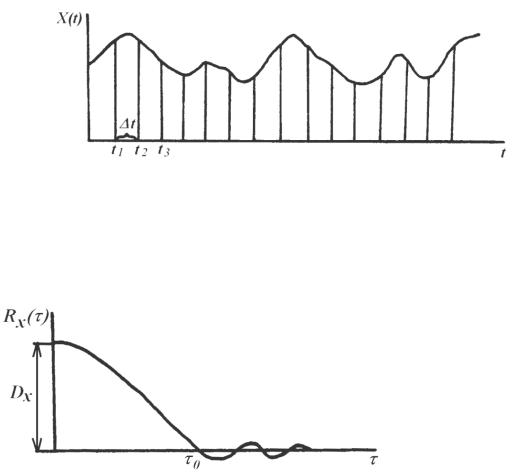
Если придать η различные значения (0, t, 2 t, 3 t) и т.д. (рис. 5.55), то после вычисления соответствующих значений Rx(0), Rx( t), Rx(2 t) и т.д. можно построить корреляционную функцию (рис. 5.56).
Рис.5.55. Эргодический стационарный случайный процесс
|
1 |
n m |
|
|
|
|
Rx ( ) |
x |
(ti )x |
(ti m ) . |
(5.111) |
||
|
||||||
|
n m |
|
|
|
||
|
|
i 1 |
|
|
|
|
Рис. 5.56. Корреляционная функция
Вместо корреляционной Rx( ) часто используют нормированную корреляционную функцию:
x( ) |
|
Rx ( ) |
|
|
. |
||
x (ti ) x |
(ti |
|
|||||
|
) |
||||||
Поскольку для стационарного случайного процесса mx(t) = const и |
|||||||
Dх(η) = const (для любого сечения), то |
|
|
|
|
|
|
|
х( ) |
Rx ( ) |
. |
(5.112) |
||||
Dх |
|
|
|||||
|
|
|
|
|
|
|
|
160
