892
.pdf



|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 7.7 |
|
|
|
|
|
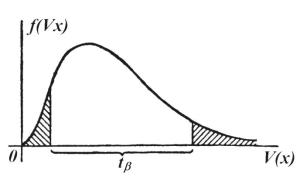
Проверка гипотезы о законе распределения времени обслуживания машин |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Время обслужива- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ния, ti, чo |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
||
|
|
|
|
|
|
|||||||||||
Наблюдаемая |
ча- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стота, mi |
|
370 |
|
244 |
147 |
95 |
58 |
35 |
22 |
14 |
8 |
7 |
|
1000 |
||
|
|
|
|
|
|
|||||||||||
ni ti |
|
185 |
|
366 |
367.5 |
332.5 |
261 |
192.5 |
143 |
105 |
68 |
66.5 |
|
2087 |
||
Накопленная |
ве- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
роятность |
факт. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ряда F (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0.37 |
|
0.614 |
0.761 |
0.856 |
0.914 |
0.949 |
0.971 |
0.985 |
0.993 |
1.000 |
|
|
Теоретическая ча- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
стота, nPi |
|
381 |
|
236 |
146 |
90 |
56 |
35 |
21 |
13 |
9 |
6 |
|
993 |
||
|
|
|
|
|
|
|||||||||||
Разность i=mi-nPi |
-11 |
|
8 |
1 |
5 |
2 |
0 |
1 |
1 |
1 |
1 |
|
|
|||
|
(Δi)2=(mi-nPi)2 |
121 |
|
64 |
1 |
25 |
4 |
0 |
1 |
1 |
1 |
1 |
|
|
||
(mi-nPi)2/nPi |
|
0.318 |
|
0.271 |
0.007 |
0.278 |
0.071 |
0 |
0.048 |
0.077 |
0.111 |
0.167 |
|
1.348 |
||
Накопленная |
ча- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стота теор. |
ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0.384 |
|
0.622 |
0.768 |
0.859 |
0.915 |
0.951 |
0.972 |
0.985 |
0.991 |
1 |
|
|
|
D |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F(x) F(x) |
0.014 |
|
0.008 |
0.007 |
0.003 |
0.001 |
0.002 |
0.001 |
0.000 |
0.001 |
0.00 |
|
|
||
|
|
|
|
|
|
|
||||||||||
230