
892
.pdf
Рис. 5.57. Нормированная корреляционная функция
У плавно протекающих случайных функциях (типа Х1(t) (рис.5.53)) расстояние η0 больше, чем, например, у резко переменных (типа Х2(t) рис. 5.61), т.е. корреляционная функция отражает внутреннюю структуру случайного процесса.
Если случайный процесс может быть отнесен к классу стационарных, то представляется возможным по корреляционной функции получить представление о частотном составе этого процесса. Для этого производят преобразование корреляционной функции по Фурье и получают так называемую спектральную плотность S(ω) случайного процесса (по частотному спектру).
Корреляционная функция Rx(η) и спектральная плотность связаны ко- синус-преобразованием Фурье:
Rx ( ) Sx ( ) cos d ;
|
0 |
|
||
Sx |
|
2 |
|
|
Rx ( ) cos d . |
||||
|
||||
|
0 |
|||
(5.113)
(5.114)
Преобразование Фурье непосредственно связано с заменой непериодических функций рядом и интегралом Фурье. С помощью этого преобразования производят спектральное разложение функций, т.е. заменяют апериодическую функцию суммой периодических гармоник с различными частотами.
Рассмотрим более подробно смысл спектральной характеристики
Sх(ω) (рис. 5.58).
Рис. 5.58. График спектральной плотности Sx(ω)
Прежде всего, можно отметить, что при η = 0 из уравнения
Rx ( ) Sx ( ) cos d
0
следует
Rx (0) Sx ( )d ,
0
161
т.е. площадь, ограниченная кривой Sx(ω) и осью частот ω, представляет собой дисперсию стационарного случайного процесса X(t).
Для какой-либо частоты ω произведение Sx(ω)dω (рис. 5.58) представляет собой площадь элементарного прямоугольника, т.е. часть дисперсии, приходящуюся на элементарный участок частот dω, около частоты ω.
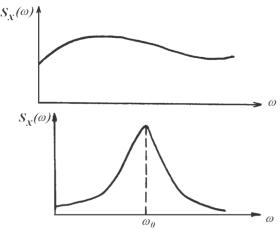
Таким образом, дисперсия Dх распадается на бесконечную сумму элементарных слагаемых по непрерывному спектру частот ω, иначе говоря, спектральная плотность стационарного случайного процесса описывает спектр его дисперсии по отдельным частотам. Чем более широк спектр, тем более беспорядочен случайный процесс (рис. 5.59, 5.60).
Рис. 5.59. Спектральная плотность широкополосного случайного процесса (белый шум)
Рис. 5.60. Спектральная плотность узкополосного случайного процесса (в процессе преобладают определенные частоты)
Спектральную плотность можно определить на основе опытных значений корреляционной функции, заменяя интеграл Фурье
|
|
|
2 |
|
|
|
|
|
Sx ( ) |
Rx ( ) cos d |
|
||
|
|
|
|
|||
|
|
|
0 |
|
|
|
конечной суммой |
|
|
|
|
||
|
|
Sx ( ) |
2 t |
R i t cos k i t , |
(5.115) |
|
|
|
|
||||
|
|
|
|
|
||
где m |
- расчетное количество точек корреляционной функции; |
|
||||
|
|
|||||
t |
|
|||||
|
|
|
|
|
|
|
k – порядковый номер коэффициента спектральной плотности. Совершенно аналогично можно получить и нормированную спек-
тральную плотность:
x Sx ( ) / Dx .
В этом случае
|
2 t |
m |
|
|
x |
i t cos k i t . |
(5.116) |
||
|
||||
|
i 0 |
|
||
|
|
|
Обычно задаются значениями ω, например, ω0 = 0; ω1 = 1; ω2 = 2; и т.д.
При ограниченном числе коэффициентов спектральной плотности шаг изменения ω определяют по соотношению / t .
Числовой пример, иллюстрирующий методику расчета характеристик, основан на использовании данных, полученных при испытаниях картофелесажалки КСМ-4 в полевых условиях. На осциллографную бумагу записаны случайные процессы изменения профиля поверхности поля, профиля дна борозды, глубины заделки клубней, колебаний сошников сажалки и заделывающих дисков при различных скоростях движения агрегата (рис. 5.61).
162
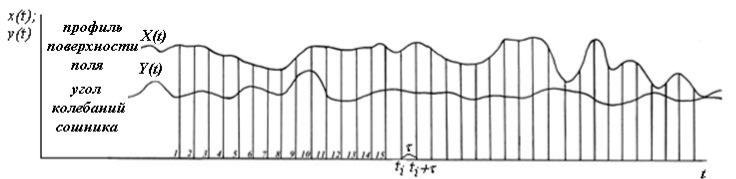
Рис. 5.61. Синхронная запись входного X(t) и выходного Y(t) процессов
Таблица 5.17
Расчет коэффициентов корреляционной функции
№ |
x(ti) |
x(ti) |
[x(ti)]2 |
x(ti)-x(ti+1) |
|
x(ti)-x(ti+2) |
x(ti)-x(ti+3) |
x(ti)-x(ti+4) |
п/п |
|
|
|
|
|
|
|
|
1 |
47 |
4 |
16 |
|
|
|
|
|
2 |
47 |
4 |
16 |
16 |
|
|
|
|
3 |
46 |
3 |
9 |
12 |
|
12 |
|
|
4 |
42 |
-1 |
1 |
-3 |
|
-4 |
-4 |
|
5 |
42 |
-1 |
1 |
1 |
|
-3 |
-4 |
-4 |
6 |
38 |
-5 |
25 |
5 |
|
5 |
-15 |
-20 |
7 |
37 |
-6 |
36 |
30 |
|
6 |
6 |
-18 |
8 |
37 |
-6 |
36 |
36 |
|
30 |
6 |
6 |
9 |
42 |
-1 |
1 |
6 |
|
6 |
5 |
1 |
10 |
48 |
5 |
25 |
-5 |
|
-30 |
-30 |
-25 |
Σ |
426 |
|
166 |
98 |
|
22 |
-36 |
-60 |
Rx(τ) |
|
|
16,6 |
0,89 |
|
2,75 |
-5,14 |
-10 |
ρx(τ) |
|
|
1 |
0,656 |
|
0,165 |
-0,310 |
-0,602 |
|
|
|
|
|
163 |
|
|
|
Измерение ординат профиля поверхности поля проверено с шагом квантования t = 0,1 c – по линиям отметчика времени осциллографа. Первый десяток измерений внесен в табл. 5.17, с помощью которой иллюстрируется порядок расчета коэффициентов корреляционной функции. Разумеется, что столь малое число измерений приведет к большим ошибкам в определении характеристик случайной функции и может быть оправдано лишь методическими соображениями.
Впоследующем расчет коэффициентов корреляционной функции и спектральной функции и спектральной плотности предусматривается определить с помощью ЭВМ по большому массиву ординат.
Втабл. 5.17 расчет коэффициентов проведен следующим образом:
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(ti ) |
|
426 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
m |
|
|
1 |
|
|
|
|
|
|
|
42,6 43 мм; |
|||||||||||||||||||
|
|
|
x |
|
|
|
n |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(ti ) x ti mx ; |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x(ti ) |
|
|
|
|
|
166 |
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
D |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16,6 мм ; |
|||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
10 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Rx (0) Dx |
16,6 |
|
|
мм; x ( ) 1; |
||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
n m |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
Rx ( ) ; |
||||||||
Rx ( ) |
|
x(ti )x(ti m) |
|
x ( ) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n m i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dх |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
R |
(0,1) |
98 |
10,89 ; |
|
|
|
|
(0,1) |
10,89 |
0,656 ; |
|||||||||||||||||||||||
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
x |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16,6 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
R (0,2) |
22 |
2,75 ; |
R (0,2) |
2,75 |
|
0,165 ; |
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
x |
|
8 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
16,6 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R (0,3) 36 5,14 ; |
|
R (0,3) 5,14 0,310 ; |
|||||||||||||||||||||||||||||||
x |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
16,6 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R |
x |
(0,4) 60 10 ; |
|
R |
x |
(0,4) 10 0,602 . |
|||||||||||||||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16,6 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При обработке массивов данных с большим числом измерений часто под сомнением остается вопрос о соблюдении условий стационарности исследуемого процесса. Чтобы исключить возможность влияния нестационарности на характеристики случайных функций, прибегают к фильтрации исходных данных. Для этой цели центрирование ординат проводят не относительно mx, а около текущего, непрерывно изменяющегося значения mx(ti), которое вычисляется по М1 ординатам, симметричным относительно ti. Число ординат М1, по которым определяется текущее значение средней высоты, называют объемом фильтра, размером или памятью фильтра.
Обычно М1 не превышает 0,1N, но в каждом исследовании выбор М1 должен быть проанализирован, так как при фильтрации возможна потеря информации о низкочастотных колебаниях процесса.
164
Помимо определения корреляционной функции и спектральной плотности отдельно входного или выходного процессов можно находить значения взаимной корреляционной функции и спектральной плотности этих процессов:
|
|
|
|
|
) |
|
|
R |
( ) M |
x(t |
) y(t |
, |
(5.117) |
||
xy |
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
т.е. взаимная корреляционная функция определяется математическим ожиданием средней величины произведения нормированных ординат входного и выходного процессов, отстоящих друг от друга на расстоянии η (рис.5.59).
Так как Rxy( ) не является четной функцией, то ее нужно вычислять не только для положительных, но и для отрицательных значений:
|
|
|
|
|
) |
|
|
R |
( ) M |
x(t |
i |
) y(t |
, |
(5.118) |
|
xy |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
или, что то же самое,
|
|
|
|
|
|
|
|
|
Ryx ( ) M y(ti ) x(ti ) . |
||||||
|
|
|
|
|
|
|
|
Вычисление нормированных |
|
|
оценок |
взаимной |
|||
функции производится по уравнениям: |
|
||||||
|
|
|
1 |
|
|
N m |
|
xy |
|
|
|
|
x(ti ) y(ti ) , |
||
|
|
|
|
|
|||
|
|
(N m) |
|||||
|
y |
i 1 |
|
||||
|
x |
|
|
|
|
||
|
|
|
1 |
|
N m |
|
|
yx |
|
|
|
|
y(ti ) x(ti ) , |
||
|
|
|
|
|
|||
|
|
(N m) |
|
|
|||
|
y |
|
|
i 1 |
|
||
|
x |
|
|
|
|
||
(5.119)
корреляционной
(5.120)
(5.121)
где N – число ординат в анализируемой реализации случайного процесса; m – число коэффициентов корреляционной функции.
В отличие от взаимной корреляционной функции обычную, определяемую по уравнению (5.110), иногда называют автокорреляционной и обо-
значают Rxx(η) или ρxx(η).
Для конкретной реализации стационарных случайных процессов X(t) и Y(t) взаимная спектральная плотность хх(ω) определяется как прямое преобразование Фурье корреляционной функции:
|
|
|
1 |
|
|
|
|
Sxy |
|
Rxy ( )e i d . |
(5.122) |
||||
|
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
Взаимная спектральная плотность является комплексной функцией |
|||||||
аргумента – частоты , поэтому |
|
|
|
||||
S |
xy |
( ) S в |
iS M , |
(5.123) |
|||
|
|
|
xy |
xy |
|
||
где Sвxy и SМxy – соответственно, вещественная и мнимая части взаимной спектральной плотности.
Поскольку в соответствии с известной формулой Эйлера
еi t cos t i sin t ,
вещественная часть Sвxy вычисляется как косинус-преобразование, а мнимая
165
SМxy – синус-преобразование Фурье:
|
|
m |
|
t |
|
|
|
|
||
Sxyв |
xy (0) ( xy yx ) cos t |
|
|
x |
|
y |
, (5.124) |
|||
|
|
|
|
|||||||
|
|
i 1 |
|
|
|
|
|
|
||
|
m |
|
t |
|
|
|
|
|
|
|
S yМх |
( xy yx ) sin t |
|
x |
y |
, |
|
|
(5.125) |
||
|
|
|
|
|
||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
где t – промежуток времени между двумя соседними ординатами в реализации изучаемого случайного процесса;
Δω – шаг изменения частоты w; / m 1 t .
Нормированная взаимная спектральная плотность определяется по
формуле: |
|
xy ( ) Sxy / x y , |
(5.126) |
где ζх и ζy – среднеквадратическое отклонение реализации случайных процессов.
Особо важное значение, отводимое определению спектральной плотности случайного процесса, связано с тем, что ее широко используют при изучении преобразования входных, возмущающих случайных функций, линейными динамическими системами сельскохозяйственных машин.
5.5.10. Информационные модели
Моделирование таких сложных динамических систем, как сельскохозяйственные машины и агрегаты, функционирующих в непрерывно изменяющихся условиях, представляет собой достаточно сложную задачу.
Аналитическое решение, даже при значительной идеализации, часто приводит к очень громоздким построениям, затрудняющим практическое использование, а иногда вообще невозможно.
Эффективным методом в таких случаях может стать построение информационных моделей. Смысл метода состоит в том, что объект моделирования представляют в виде некоторого оператора А или W («черного ящика»), а его свойства определяют по соотношению входных X(t) воздействий и выходных Y(t) параметров (рис.5.2). О принципиальной возможности такого подхода при неслучайных, стандартных воздействиях (единичных скачков, гармонических колебаний) уже было указано ранее. Осуществить такие воздействия обычно удается лишь на отдельные рабочие органы.
Свойства оператора W для сложных машин и агрегатов приходится определять по соотношению входных и выходных параметров, представляющих собой случайные функции.
Так, пусть на вход линейной динамической системы (т.е., например, механической системы, описываемой линейными дифференциальными уравнениями) поступает стационарная случайная функция X(t), а реакция системы представляет собой случайную функцию Y(t) (рис. 5.62). Например, сошник сажалки перемещается по полю, микронеровности которого
166
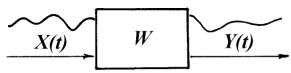
описываются случайной функцией X(t). В качестве выходной Y(t) можно рассматривать глубину бороздки.
Рис. 5.62. Схема одномерной модели преобразования входных возмущающих функций линейной динамической системой
Поскольку характеристиками случайных функций являются неслу-
чайные функции mx(t), Rx( ), Sx( ) и my(t), Ry( ), Sy( ), то, прежде всего, можно рассмотреть задачу об определении реакции системы на неслучай-
ные воздействия f(t).
При анализе характеристик линейных динамических систем было отмечено, что при воздействии на нее стандартными возмущениями (допустим, в виде гармонических колебаний определенной частоты), реакцией системы оказываются колебания с той же частотой, но с измененной амплитудой и сдвигом фаз.
Например, уравнения малых колебаний сошника сеялки (5.26) в терминах «вход» х(t) и «выход» у(t) может быть записано в виде:
T12 y(t) T2 y(t) y(t) k x(t) ,
где Т1, Т2 и k – соответственно, инерционный, демпфирующий коэффициенты и коэффициент усиления.
Реакцию на входную гармонику
x(t) ei t
можно представить тоже в виде гармонического колебания, но умноженного на некоторый комплексный множитель:
y(t) Ф(i )ei t . |
(5.127) |
Для определения того, что представляет собой этот комплексный множитель Ф(i ) необходимо значения y(t) и x(t) подставить в линейное дифференциальное уравнение:
T 2 |
Ф(i ) ei t |
|
T Ф(i ) ei t |
|
Ф(i ) ei t k ei t . |
|||||||
|
|
|||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
После дифференцирования, деления правой и левой части на ei t и |
||||||||||||
вынесения за скобки комплексного множителя Ф(i ) можно получить: |
||||||||||||
|
Ф(i ) T 2 (i )2 Т |
2 |
(i ) 1 k |
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
. |
(5.128) |
|
|
|
|
|
|
|
|
|
|
|
||
|
Ф(i ) T 2 (i )2 |
|
|
|
|
|
|
|||||
|
Т |
2 |
(i ) 1 |
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
||
Но это не что иное, как частотная функция линейной динамической системы W(i ) (5.30).
Таким образом, если на вход линейной динамической системы поступают гармонические колебания вида ei t, то на выходе окажутся гармонические колебания того же вида, умноженные на частотную характеристику системы.
Следует напомнить, что частотная функция как комплексное число
167

(рис. 5.27) может быть представлена в виде вектора с модулем А( ) и угла сдвига фаз ( ).
Спектральную плотность входного и выходного случайных процессов, как было уже отмечено, представляет собой разложение дисперсии по отдельным частотам (рис. 5.58).
Произведение любой ординаты Sx( ) на d геометрически может представлять собой прямоугольник, составляющий часть дисперсии Dx, т.е. определяет вклад в общую дисперсию колебаний системы с частотой .
Каждой гармонике входного процесса можно привести в соответствие выходное колебание с той же частотой, но измененное по амплитуде и сдвинутое по фазе, или в общем случае умноженное на частотную функ-
цию W(i ) по уравнению (5.30) или равную ей Ф(i ). |
|
Если связать все элементарные участки дисперсии |
Sx ( ) dt вход- |
ной и выходной функций спектральной плотности, то можно получить |
|
Sy ( ) A( ) 2 Sx ( ) , |
(5.129) |
так как дисперсия определяется квадратом случайной величины, а в данном примере – модулем амплитудно-частотной характеристики.
Определение коэффициентов передаточных и частотных функций на основе экспериментальных данных
Достаточно наглядным примером может быть продолжение исследования колебаний сошника.
Уравнение (5.129) может явиться основой для построения экспери-
ментальной кривой:
A( ) 2 S y ( ) . Sx ( )
Поскольку уравнение частотной функции сошниковой группы известно (5.38),
W i |
|
|
k |
, |
|
|
|
|
|
||
|
i 2 |
T i 1 |
|||
T 2 |
|
||||
1 |
|
2 |
|
|
|
то квадрат модуля частотной функции вычисляют по формуле:
2 |
|
k |
|
|
|
A |
|
|
|
. |
(5.130) |
1 T 2 2 |
T 2 |
||||
|
1 |
2 |
|
|
|
Если на экспериментальной кривой квадрата модуля частотной |
|||||
функции взять значения A A( 1) 2 и B A( 2 ) 2 |
для двух значений ча- |
||||
стот 1 и 2, а также определить k при = 0, то для определения коэффициентов передаточной функции необходимо решить систему уравнений второго порядка:
168

|
|
|
|
A |
|
|
|
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
T2 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 T12 12 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 T1 |
2 |
|
T2 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(k 2 |
A) 2 |
|||
B 2BT 2 2 |
BT 4 4 |
2BT 2 |
2 BT 4 2 2 |
|
|
|
|
|
2 |
k 2 , |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
1 |
2 |
|
1 |
2 |
|
|
1 |
2 |
|
|
1 |
1 |
|
|
2 |
|
|
|
|
|
A 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
BT 4 2 |
|
2 |
2 k 2 |
B |
B(k 2 A) 22 |
, |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
2 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
A 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
A 2 |
B B 2 A k 2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
T1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
AB 2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 T |
4 , |
T T 2 |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
A k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
T 2 |
2T 2 |
T 4 2 |
|
; |
|
T T 2 . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
1 |
|
|
1 |
1 |
|
|
A |
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После определения k, Т1 и Т2 находят теоретическое значение функции A 2 по уравнению (5.130). Если теоретическая и эксперименталь-
ная кривые достаточно близки друг к другу, то коэффициенты передаточной функции можно считать определенными. В случае значительного отличия теоретической и экспериментальной кривых, берут другие значения А и В, и повторяют расчет.
Опыт определения коэффициентов данным методом показал, что ошибки при этом оказываются большими, и он рекомендуется лишь для тех случаев, когда X(t) и Y(t) слабо коррелированны. При достаточно высоком уровне корреляции между входными и выходными процессами одномерной модели экспериментальные значения амплитудно-частотной характеристики рекомендуется вычислять по выражению:
A( ) 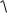
 Sxyв ( ) / Sx ( ) 2 SxyM ( ) / Sx ( ) 2 ,
Sxyв ( ) / Sx ( ) 2 SxyM ( ) / Sx ( ) 2 ,
а коэффициент усиления –
kSxy (0) . Sxx (0)
Вэтом случае экспериментальные значения А, В, ω1, ω2 необходимо
взять на кривой, построенной по уравнению (5.130).
Если в результате расчета окажется, что по соотношению Т1 и Т2 сошник будет представлять собой колебательное звено (Т2 < 2Т1), то необходимо изменить его параметры (момент инерции, силу сжатия пружины, размеры) так, чтобы перевести в апериодическое звено второго порядка. Зависимости коэффициентов от параметров конструкций, полученные при выводе уравнения малых колебаний сошников, позволяют провести целенаправленное изменение коэффициентов передаточной функции.
169
Следует отметить, что представленная методика расчета в определенной мере является упрощенной, так как ограничена рамками учебного пособия.
Тем, кто желает ознакомиться с деталями расчетов, например, с обоснованием функций спектральной плотности, аппроксимацией корреляционных функций и функций спектральной плотности и т.д., рекомендуется обратиться к специальным источникам [23], [24], [41], [42].
Расчет характеристик случайных функций профиля поверхности поля и колебаний сошника может быть выполнен по программе «Сеялка (Sejlka)», разработанной на кафедре сельскохозяйственных машин Пермской ГСХА.
Результаты расчета могут быть использованы для определения коэффициентов передаточной и частотной функции.
Фрагмент результатов одного из расчетов приводится в качестве примера.
Профиль поверхности поля является случайным и может быть охарактеризован корреляционной функцией и функцией спектральной плотности.
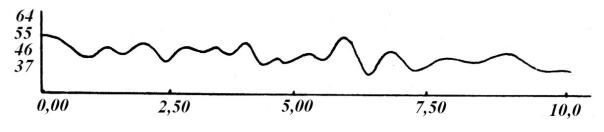
Случайная функция, описывающая свойства поля при движении по нему агрегата с заданной скоростью, на основании опытных данных может принять следующий вид X(t).
Рис.5.63. Случайная функция X(t), характеризующая профиль поверхности поля
Обработка случайной функции Х(t)
Среднее без фильтрации 46,68. Дисперсия без фильтрации 25,20. Дисперсия с фильтрацией 19,2300.
Коэффициенты корреляционной функции
Без фильтрации ординат |
С фильтрацией ординат |
R(0) = 1,00000 |
R(0)= 1,00000 |
R(1) = 0,74239 |
R(1)= 0,59493 |
R(2) = 0,31673 |
R(2)=-0,07851 |
R(3) =-0,00152 |
R(3)=-0,52994 |
R(4) =-0,12343 |
R(4)=-0,57853 |
170
