
892
.pdf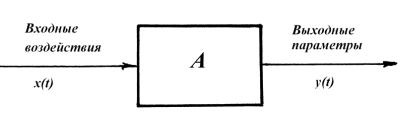
y(t) A x(t) .
Рис. 5.2. Схема информационной модели
Преобразование А может быть любого вида и любой сложности. В наиболее простых случаях, например, умножение на заданный множитель (усилитель, передаточные механизмы), дифференцирование, интегрирование и т.д.
Правило А, по которому функция x(t) преобразуется в y(t), называют оператором. Если оператор А определяют по соотношению x(t) и y(t), то по сути дела и находят информационную модель.
Внастоящее время основную часть моделей составляют математические. Классификация этих моделей весьма затруднительна, поскольку существует множество оснований классификации, например:
- форма представления моделей; - способ получения моделей; - назначение моделей;
- способ прогнозирования результатов; - характер отображаемых свойств; - степень абстрагирования и т.д.
Одна из возможных классификаций математических моделей изображена на рис. 5.3, представляющая собой модифицированную схему, используемую при исследованиях технических систем [17].
Вэтой схеме по форме представления различают инвариантные, алгоритмические, аналитические и графические модели.
Инвариантные модели обычно бывают в виде систем алгебраических или дифференциальных уравнений.
Алгоритмические модели записываются в виде алгоритма – последовательности вычислений. Сюда же относятся алгоритмы программ для ЭВМ.
Аналитические модели – это те, для которых найдены явные зависимости искомых переменных от заданных величин. Такие модели получают на основе физических законов, либо в результате прямого интегрирования исходных дифференциальных уравнений. К ним относятся регрессионные модели, получаемые на основе результатов эксперимента.
Графические модели бывают представлены в виде эквивалентных схем, диаграмм, циклограмм, графов и т.п.
61
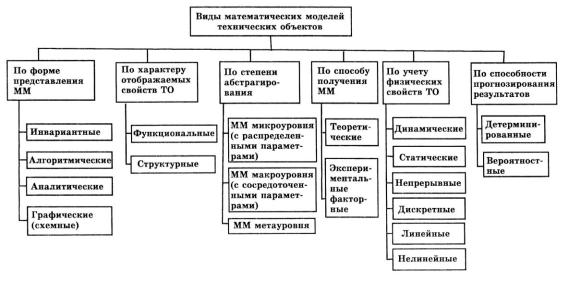
Рис. 5.3. Классификация математических моделей
По характеру отражаемых свойств объектов модели разделяют на структурные и функциональные.
Структурные модели, которые отображают связи между основными структурными единицами (элементами) системы. Их обычно представляют в форме таблиц, матриц. Элементы структурных моделей отличаются функциональными или конструктивными признаками.
Функциональные модели, это те которые описывают процессы функционирования исследуемых объектов и имеют форму систем уравнений. Эти модели могут быть построены на основе законов физики, химии, биологии, механики или быть формальными – экспериментальными. Экспериментальные модели не учитывают всего комплекса физических свойств элементов системы, а лишь устанавливают обнаруженную в процессе эксперимента связь между отдельными параметрами объекта.
По степени абстрагирования различают модели на микро-, мета- и макроуровне.
Модели на метауровне. Метауровень соответствует начальным стадиям исследования или проектирования, на котором осуществляется науч- но-технический поиск и ведется разработка технического предложения. Для построения математических моделей метауровня используют методы морфологического анализа и синтеза, математической логики, теории автоматического управления, теории массового обслуживания, теории игр, теории графов, теории информации;
Модели на макроуровне описывают динамические системы с сосредоточенными параметрами. Обычно это системы обыкновенных дифференциальных уравнений. Эти модели используют для определения параметров технического объекта и его функциональных элементов.
Модели на микроуровне. Объект представляется как сплошная среда с распределенными параметрами.
На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элементами.
62
Примерами таких элементов являются рамы, панели, отдельные детали. Их проектирование основано на анализе сложнонапряженного состояния деформированных элементов. Методы механики сплошной фрезы широко используются в гидравлике и аэродинамике, когда изучается сложное движение элементов среды, с учетом непрерывно изменяющихся полей сил, напряжений, скоростей, завихрений и т.п.
Модели на клеточном и молекулярном уровне используют в биологии,
химии для описания соответствующих взаимодействий.
По способу получения моделей их разделяют:
-на теоретические, построенные исключительно математическими методами;
-экспериментальные, в том числе полученные использованием методов многофакторного эксперимента, закончившегося составлением уравнений регрессии;
-на использующие методы вычислительного эксперимента. («Экс-
перимент с моделью».). Вычислительным экспериментом называется методология и технология исследований, основанная на применении прикладной математики и компьютеров как технической базы использования математических моделей.
Возможности современных ЭВМ позволяют проанализировать математические модели в широком диапазоне изменений факторов и представить их в виде цифровых рядов, позволяющих количественно оценить их значимость. Вычислительный эксперимент незаменим при исследовании глобальных климатических систем, когда постановка эксперимента невозможна; при исследовании ранимых объектов, которые в результате широкого диапазона изменения факторов можно привести к катастрофическим, необратимым результатам.
В учебном процессе исследование моделей вместо реальных объектов позволяет значительно расширить представление о процессе за весьма ограниченное учебное время. Практически все программы кафедры СХМ Пермской ГСХА, предназначенные для анализа технологических процессов, осуществляемых сельскохозяйственными машинами, используют метод вычислительного эксперимента;
-на имитационные модели, которые часто разрабатывают для создания последовательности случайных величин или случайных функций с определенными законами распределения или характеристиками. Эти законы и характеристики обычно соответствуют тем, которые имеют внешние возмущения при реальной эксплуатации машин. Имитационные модели часто используют в командных устройствах, воспроизводящих параметры реальных воздействий в лабораторных условиях. Имитационные модели могут сочетаться с методами вычислительного эксперимента, если некоторые параметры процесса являются случайными (например, физикомеханические свойства обрабатываемого материала, распределения семян, растений и др.).
По учету физических свойств объектов существуют модели:
-динамические (т.е. зависимые от времени);
63
-статические (независимые от времени);
-непрерывные;
-дискретные;
-линейные (описываемые линейными дифференциальными уравне-
ниями).
По способу прогнозирования результатов различают модели:
-детерминированные (неслучайные);
-вероятностные (стохастические).
По назначению модели разделяют:
-на дискриптивные (описательные), разработанные для исследования структуры того или иного объекта;
-кибернетические (управляющие), разработанные для исследования управляющих воздействий и обоснования их рациональных параметров;
-оптимизационные – создаваемые для оптимизации технологических процессов.
5.2. Физическое моделирование. Основные понятия
Первой ассоциацией понятия модели обычно оказываются уменьшенные копии машины или сооружения. Желание провести исследование на этих уменьшенных вариантах вполне естественно, так как изготовление таких моделей значительно дешевле оригиналов, и для их исследования не нужны большие экспериментальные сооружения, мощные приводные установки и т.д. и т.п.
Попытки испытаний на моделях проводились еще в античные времена, но тогда же было обнаружено, что полномасштабные образцы машин и сооружений ведут себя иначе. Исторические корни осознания причин такого несоответствия и разработка методов научного моделирования восходят к работам Леонардо да Винчи, Г. Галилея, И. Ньютона, И. Кулибина, Ж. Фурье, О. Коши, Л. Эйлера и др.
Значительный вклад в теорию подобия и моделирования внесли наши соотечественники – академики В.Л. Кирпичев, Л.И. Седов, А.Н. Крылов, В.П. Горячкин, Н.Д. Лучинский.
Теория моделирования решает такие задачи, как обоснование требований к модели, воспроизводящей работу оригинала и правила переноса результатов исследований на модели – на оригинал.
Широкое применение моделирование находит в учебной практике. Модели могут использовать для демонстрации физических законов,
технологических процессов, действия новых разработок, установок и т.п. Моделирование может быть полным (когда обеспечивается подобие
движения материи в основных формах ее существования, т.е. в пространстве и времени), неполным (когда подобие устанавливается между некоторыми функциями или обобщенными характеристиками) и приближенным (когда некоторые параметры, не оказывающие решающего действия на протекание процесса, моделируются приближенно или совсем не моделируются). Разумеется, что в этом случае возникает необходимость в оценке возможной погрешности.
64

5.2.1. Критерии подобия
Одним из основных понятий в физическом моделировании является
подобие.
Подобие явлений означает, что данные о протекании процессов, полученные при изучении одного из них, можно перенести на все подобные данному, путем пересчета характеристик с помощью критериев подобия.
Теорема о механическом подобии впервые сформулирована И. Ньютоном в 1636 г. в книге «Математические начала натуральной философии».
На основании теоремы подобия он вывел закон сопротивления жидкости движущемуся в ней твердому телу. Закон подобия И. Ньютона предопределяет механическое подобие систем, включающее в себя геометриче-
ское, кинематическое и динамическое подобия.
Под геометрическим подобием понимается пропорциональность линейных размеров и равенство угловых параметров. Линейный масштаб К
можно найти как |
К |
|
м |
, |
|
н |
|
||
|
|
|
|
где ℓм – линейные размеры модели; ℓн – линейные размеры натуры.
Под кинематическим подобием понимают изменяющиеся во времени системы, совершающие геометрические подобные перемещения в промежутки времени, находящиеся в постоянном соотношении:
|
|
|
|
|
|
|
|
|
|
|
t |
M |
|
t |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
Kt |
|
|
|
M |
|
|
|
|||
|
|
|
|
|
|
|
|
|
t |
H |
t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
||
|
где t |
, t |
H |
, |
|
, |
|
– время прохождения частицей (телом) отрезков ℓ |
м |
||||||||||
|
M |
|
|
tM |
|
tH |
|
|
|
|
|
|
|
|
|
|
|||
ℓн |
, причем |
М / Н М / Н К . |
|
|
|
|
|
|
|||||||||||
M |
Н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В кинематически подобных системах отношения скоростей и ускоре- |
||||||||||||||||||
ний в соответствующие моменты времени постоянны, т.е. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
К |
VM |
idem; K |
|
|
aM |
idem . |
|
||||
|
|
|
|
|
|
|
|
V |
VH |
|
|
|
|
|
a |
|
aH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При динамическом подобии соотношения между соответствующими силами, действующими в обеих геометрически подобных системах, должны быть одинаковыми:
К p PM mM aM idem . PH mH aH
Частные критерии динамического подобия удобно представлены в виде таблицы С.Дж. Клайна [18].
Кроме критериев, указанных в табл. 5.1, при моделировании используются и другие критерии, например, В. Струхаля, Кармане, Ж. Фурье, Био, Дамкелера и др., характеризующие кинематическое или динамическое подобие [18].
65
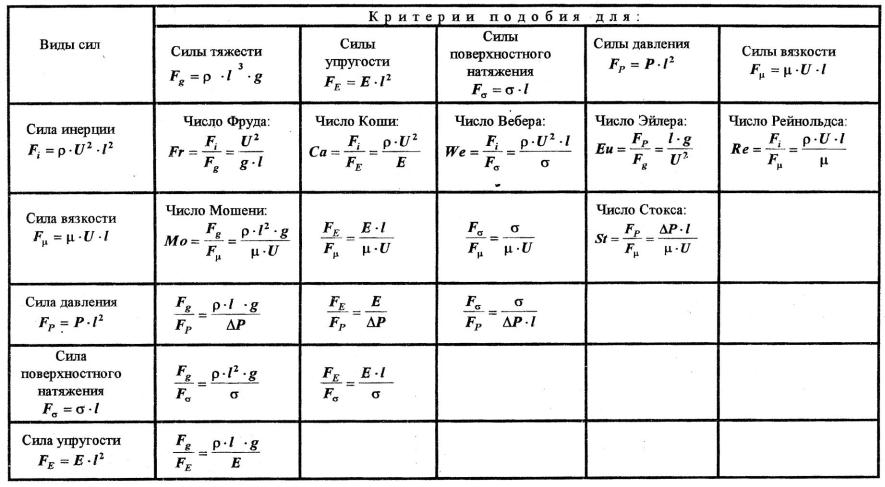
Таблица 5.1
Критерии подобия для сил различной физической природы
66

При наличии динамического подобия очень легко устанавливается связь между всеми кинематическими и динамическими характеристиками систем.
В качестве примера использования критериев подобия можно представить лабораторный почвенный канал кафедры «Сельскохозяйственные машины» Пермской ГСХА (рис. 5.4), в котором изучается процесс взаимодействия моделей рабочих органов плугов с обрабатываемой средой.
Для этой цели изготовлены модели лемешно-отвальной поверхности культурного, полувинтового и винтового вида и дискового плуга в масшта-
бе К |
|
|
м |
0,2 . |
|
|
|
н |
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Для определения коэффициента кинематического подобия К |
|
|
tM |
||
|
|
t |
tн |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
необходимо определить время подъема частиц почвы, отбрасываемых отвалом.
Высота подъема частиц составляет |
H |
gt 2 |
, а время подъема их для |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2HM |
|
|
|
|
2H H |
|
|
|
|
HM |
|
|
|
|
|
||||||
модели и натуры - t |
M |
|
|
, t |
H |
|
|
, отсюда K |
t |
|
|
K |
|
. |
||||||||||
|
|
|
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
g |
|
|
|
g |
|
|
|
H H |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 5.4. Лабораторный почвенный канал
Рабочие органы натуры и модели, будучи геометрически подобными и обладая одной и той же материальной структурой, имеют массы, пропорциональные объемам, - mM C M lM3 ; mH C H lH3 .
Тогда соотношение между массами модели и натуры составит:
|
|
|
m |
M |
|
C |
l 3 |
l 3 |
K 3 . |
|
K |
|
|
|
|
|
M M |
|
M |
||
m |
|
|
|
|
|
|||||
|
|
m |
|
|
C |
l 3 |
l 3 |
l |
||
|
|
|
H |
|
|
|||||
|
|
|
|
|
|
H H |
H |
|
||
Выбор обрабатываемого материала при моделировании технологического процесса так же важен, как и определение коэффициентов подобия
67
геометрических и кинематических параметров машины. Условия подобия обрабатываемого материала можно записать в виде
θм = θн; fm = fn ;
dl m
d
,l n
где θ – коэффициент внутреннего трения; f – коэффициент внешнего трения;
d – линейный размер частиц;
l – линейный размер рабочего органа.
Как следует из этих формул, коэффициенты внутреннего и внешнего трения должны быть равными, а максимальный размер частиц для обработки моделью составляет:
d |
|
d |
|
lM |
d |
|
K |
. |
M |
H |
|
H |
|||||
|
|
lH |
l |
|
||||
|
|
|
|
|
|
|
||
Твердость (плотность) почвы определяется по соотношениям:
M hM ; H hН .
F F
Тогда коэффициент твердости составит:
K m hM Kl ,
n hH
где hм – величина деформации почвы-модели; hН – величина деформации почвы-натуры.
Основные коэффициенты подобия приведены в табл. 5.2.
Таблица. 5.2
Основные коэффициенты подобия при исследовании моделей рабочих органов плуга в лабораторном почвенном канале
Коэффициенты |
Kl |
Кt |
|
Km |
Kv |
|
Ka |
Kp |
Kd |
Kp |
Kn |
||
Значения |
0,2 |
|
|
|
Kl3 |
|
|
|
l |
Kl3 |
Kl |
Kl |
K 3,5 |
|
Kl |
|
|
Kl |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
Указанные коэффициенты учтены при построении лабораторного почвенного канала и его рабочих органов.
Лабораторный почвенный канал (рис. 5.4. и 5.5) включает ящик с почвой, несущую раму, тяговую станцию с пультом управления и динамометрическую тележку.
Рама установлена сверху ящика и может перемещаться в поперечном направлении из крайнего левого в крайнее правое положение с фиксированием в прорезях верхнего контура ящика.
На раме смонтирована тяговая станция, которая обеспечивает движение динамометрической тележки на трех скоростях: 0,671; 0,894 и 1,118м/с, что соответствует рабочим скоростям тракторного пахотного агрегата 5,4; 7,2 и 9 км/ч.
Динамометрическая тележка опирается роликами на несущий пояс
68

рамы. На тележке смонтированы: суппорт, пружинный динамометр и лентопротяжный барабан с самописцем.
Суппорт служит для крепления рабочих органов и позволяет регулировать глубину хода их от 0 до 6 см. Суппорт перемещается вдоль тележки винтом и имеет три фиксированных положения. Пружинный динамометр рассчитан на максимальное усилие 50Н, что соответствует тяговому сопротивлению корпуса натурального образца 6250Н.
Рис. 5.5. Динамометрическая тележка
Перед испытанием динамометр тарируют.
Образец тарировочной диаграммы, калибр пружины и образец динамограммы моделей представлены на рис.5.6.
Практика использования лабораторного почвенного канала показала, что в нем достигается только приближенная степень подобия реальному процессу вспашки. Основной причиной ошибок является несоответствие почвы канала условиям физического моделирования.
Проф. В.С. Кировым [19] подобран состав моделируемой почвы, эквивалентной оригиналу. В состав ее входит торф, песок, глина, масло веретенное. Грунт необходимо уплотнить до γ = 1,2…5,7 г/см3. Подготовить такой грунт в достаточном количестве и, особенно, поддерживать необходимое состояние в продолжительное время затруднительно. Положительной стороной такой лабораторной работы является хорошая иллюстрация теории подобия И. Ньютона и, в конечном счете, первой теоремы подобия, согласно которой подобные явления имеют одинаковые критерии подобия.
Существенный вклад в теорию подобия внес Ж. Фурье в работе «Аналитическая теория» теплопроводимости, где он указывал на свойство размерной однородности всех членов уравнений математической физики.
Таким образом, были заложены основы теории размерностей в физическом моделировании.
69
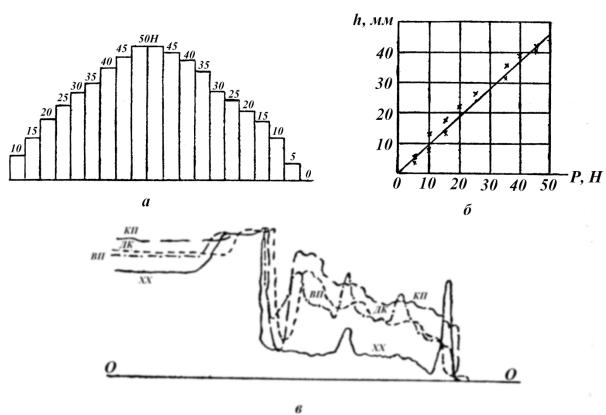
Рис. 5.6. Тарировочная диаграмма (а), калибр пружины (б) и образец динамограммы моделей (в).
КП – корпус с поверхностью культурного вида; ВП – корпус с винтовой поверхностью; ДК – дисковый корпус; ХХ – проход модели корпуса в открытой борозде (холостой ряд).
Критерии подобия стало возможным определять различными путями: либо из условий тождественности уравнений, описывающих процессы, или из анализа размерностей, разновидностью которого является метод нулевых размерностей. Основой анализа размерности является положение о том, что все математические равенства, выражающие связь между физическими величинами, должны быть размерно-однородными или однородными по размерности.
Это означает:
-размерность правой части равенства должна быть такой же, как и размерность левой части того же равенства;
-складывать и вычитать можно только величины одной размерности. Эти очевидные правила (вряд ли кому-нибудь представится возмож-
ность складывать один килограмм с одним метром) позволяют получать нетривиальные результаты, что вызывает у начинающих исследователей настороженное отношение к анализу размерностей. С одной стороны, результаты получаются как бы «из ничего», из бесспорных предпосылок, которые не похожи на привычный фундамент физических наук; с другой стороны, результаты не имеют окончательных физических зависимостей, они требуют дополнительного, чаще всего экспериментального изучения явлений.
70
