659

′

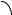
Рис. 2.30. Преобразование координат при параллельном сдвиге осей с последующим их поворотом

Учитывая формулы преобразования координат при параллельном сдвиге осей, можно записать следующую связь между координатами точки

в старой и вспомогательной системах координат:

{ = + ′′,= + ′′.

Затем, учитывая формулы преобразования координат при повороте осей, можно записать следующую связь между координатами точки во

вспомогательной и новой системах координат:

′′ = ′ cos − ′ sin , { ′′ = ′ sin + ′ cos .

Далее, учитывая полученные и предыдущие выражения, можно записать связь между координатами точки в старой и новой системах коор-

динат:

= ′ cos − ′ sin + , { = ′ sin + ′ cos + .

Эти формулы называют формулами преобразования координат при параллельном сдвиге осей с последующим их поворотом. Они позволяют найти координаты точки в старой системе, зная координаты точки в новой системе.

Получим формулы, позволяющие найти координаты точки в новой системе, зная координаты точки в старой системе. Для этого решим полученную систему линейных алгебраических уравнений по правилу Крамера относительно неизвестных ′ и ′. Перепишем систему в виде:

51

Таким образом:

′ = ( − ) cos + ( − ) sin , { ′ = −( − ) sin + ( − ) cos .

Эти формулы также называют формулами преобразования координат при параллельном сдвиге осей с последующим их поворотом. Они поз-

воляют найти координаты точки в новой системе, зная координаты точки в старой системе.

Пример 2.33. Определить старые координаты нового начала координат и угол , на который повёрнуты оси, если формулы преобразования ко-

ординат заданы следующими равенствами: = √22 ′ + √22 ′ + 5, =

= − √22 ′ + √22 ′ − 3.

Решение. Сравним данные формулы с формулами преобразования координат при параллельном сдвиге осей с последующим их поворотом:

Ответ: = − 4 , ′(5; −3).

Пример 2.34. Написать формулы преобразования координат, если координатные оси повёрнуты на угол = 6 , начало координат перенесено

в точку ′(−2; 3). Масштаб сохранён.

Решение. Воспользуемся формулами преобразования координат при параллельном сдвиге осей с последующим их поворотом:

= ′ cos − ′ sin + , = ′ sin + ′ cos + .

Учитывая, что = 6 , = −2, = 3, получаем:

= ′ cos − ′ sin + = ′ cos 6 − ′ sin 6 − 2 = √23 ′ − 12 ′ − 2,= ′ sin + ′ cos + = ′ sin 6 + ′ cos 6 + 3 = 12 ′ + √23 ′ + 3.

Ответ: = √23 ′ − 12 ′ − 2, = 12 ′ + √23 ′ + 3.

Пример 2.35. Дана точка (1; −2). Найти координаты этой точки в новой системе, если начало координат перенесено в точку ′(−2;3), оси

координат повёрнуты на угол = 34 , масштаб сохранён.

Решение. Для применения формул преобразования координат при параллельном сдвиге осей с последующим их поворотом, найдём cos и sin :

52

Тогда координаты точки в новой системе координат:

′ = ( − ) cos + ( − ) sin = (1 − (−2)) 4 + (−2 − 3) 3 = − 3 ,

55 5

′ = −( − ) sin + ( − ) cos = −(1 − (−2)) 35 + (−2 − 3) 45 =

=− 295 .

Таким образом, координаты точки в новой системе: (− 35 ; − 295 ).

Ответ: (− 35 ; − 295 ).

Контрольные вопросы

1.Как определяется система координат на плоскости?

2.Дайте определение координат точки в декартовой прямоугольной системе координат на плоскости?

3.Запишите формулу нахождения расстояния между двумя точками на плоскости.

4.Дайте определение проекции направленного отрезка на координатные оси.

5.Запишите формулы нахождения проекции направленного отрезка на координатные оси через координаты его начала и конца.

6.Запишите формулы нахождения проекции направленного отрезка на координатные оси через его длину и полярный угол.

7.Запишите формулу нахождения полярного угла отрезка через координаты его начала и конца.

8.Запишите формулу нахождения координат точки на плоскости, которая делит отрезок в заданном отношении. Запишите также частный случай, когда точка является серединой отрезка.

9.Запишите формулу вычисления площади треугольника через координаты его вершин.

10.Запишите условие расположения точек на одной прямой через координаты этих точек.

11.Как определяется полярная система координат?

12.Дайте определение координат точки в полярной системе коор-

динат?

13.Запишите формулы, выражающие прямоугольные координаты точки через её полярные координаты.

14.Запишите формулы, выражающие полярные координаты точки через её прямоугольные координаты.

15.Запишите формулы преобразования координат при параллельном сдвиге осей.

16.Запишите формулы преобразования координат при повороте

осей.

53

17. Запишите формулы преобразования координат при параллельном сдвиге осей с последующим их поворотом.

Упражнения

1.Построить точки (−3; 2), (−4; −1), (5; 4), (7; −3),

(−1; 0), (2; 0), (0; 6), (0; −4), (√5 + 1; −2), (6,2; 0), (1; 2√3).

2.Найти координаты точки, симметричной точке (3; 2) относительно: 1) оси абсцисс; 2) оси ординат; 3) начала координат; 4) биссектрисы первого координатного угла; 5) биссектрисы второго координатного угла.

3.Найти точки, абсцисса которых равна 2, а ордината определя-

+ 2;

5)= 2 .

4.В таблице приведены сведения о результатах контрольной ра-

боты 100 студентов одного курса. Контрольная работа оценивалась по 10балльной системе. 32 1

Изобразить точками зависимость между баллом и числом студентов, получивших этот балл. Точки соединить плавной кривой.

пр 1 2 = 5, пр 1 2 = −4. Зная, что начало отрезка находится в точке1(−2; 3), найти координаты его конца.

13.Вычислить проекции отрезка на координатные оси, зная, что длина отрезка равна 12, полярный угол равен 23 .

14.Даны две точки (1; −5) и (4; −1). Найти проекцию отрезка

̅̅̅̅ на ось, которая составляет с осью абсцисс угол = − 6 .

15.Точки (1; 1), (−3; −7), (5; 9) лежат на одной прямой. Определить, в каком отношении точка делит отрезок ̅̅̅̅С.

54

16.Даны две точки 1(1; −1) и 2(4; 6). Найти координаты

точки , которая делит отрезок ̅̅̅̅̅̅̅̅1 2 в отношении = 2.

17. Даны две точки 1 −3; 4) и 2(−1; −6). Найти координаты

середины отрезка ̅̅̅̅̅̅̅̅.

1 2

18. Даны концы (3; −5) и (−1; 1) однородного стержня. Определить координаты его центра масс.

19.Центр масс однородного стержня находится в точке (1; 4), один из его концов в точке (−2; 2). Определить координаты точки – другого конца этого стержня.

20.Даны вершины треугольника (1; 4), (3; −9), (−5; 2). Определить длину его медианы, проведённой из вершины .

21.Даны вершины треугольника (−5; 0), (−2; −1), (1; 4). Определить точку пересечения его медиан. Указание. Искомая точка делит

(0; 5). Определить четвёртую вершину .

24.Даны вершины треугольника (3; −5), (−3; 3), (−1; −2). Определить длину биссектрисы его внутреннего угла при вершине .

25.Прямая проходит через точки 1(−12; −13) и 2(−2; −5). На

(−2; 14), (4; −2), (6; −2), (6; 10). Определить точку пересечения его диагоналей и .

27. Даны вершины однородной прямоугольной пластины:

1( 1; 1), 2( 2; 2), 3( 3; 3), 4( 4; 4). Определить центр масс пла-

стины. Указание. Центр масс прямоугольника находится в точке пересечения его диагоналей.

28.Однородная пластинка имеет форму квадрата со стороной, равной 12, в которой сделан квадратный вырез, прямые разреза проходят через центр квадрата, оси координат направлены по рёбрам пластинки. Определить центр масс этой пластинки. Указание. Центр масс прямоугольника находится в точке пересечения его диагоналей.

29.В точках 1( 1; 1) и 2( 2; 2) помещены массы 1 и 2 соответственно. Найти центр тяжести этой системы масс.

Указание. Из механики известно, что центр тяжести системы двух

30. В точках 1( 1; 1), 2( 2; 2), 3( 3; 3) помещены массы

1, 2, 3 соответственно. Найти центр тяжести этой системы масс. Указание. Сначала найти центр тяжести двух материальных точек, а

затем центр тяжести найденной точки и третьей данной точки.

55

31.В трёх точках (7; 1,5), (6; 7) и (2; 4) помещены грузы в 60г, 100 г и 40 г соответственно. Определить центр тяжести этой системы. Указание. Воспользоваться результатом задачи 30.

32.Даны три точки 1(3; −4), 2(−2; 3) и 3(4; 5). Найти пло-

щадь треугольника 1 2 3.

33.Даны три вершины параллелограмма 1(−2; 3), 2(4; −5) и3(−3; 1). Найти площадь параллелограмма.

34.Площадь параллелограмма равна 12. Две его вершины нахо-

дятся в точках (−1; 3) и (−2; 4). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси абсцисс.

35.Выяснить, лежат ли на одной прямой три данные точки:

1)1(0; 5), 2(2; 1) и 3(−1; 7); 2) 1(3; 1), 2(−2; −9) и 3(8; 11);

3)1(0; 2), 2(−1; 5) и 3(3; 4).

36.Точка, двигаясь прямолинейно, прошла через точки (5; 5) и

(1; 3). Определить точку, в которой она пересечёт ось абсцисс. Указание. Определить абсциссу искомой точки ( ; 0) из условия, что эта точка должна лежать на одной прямой с двумя данными точками.

37. Известны координаты двух вершин треугольника (3; 1) и(1; −3), а третья вершина лежит на оси . Площадь треугольника равна 3. Найти координаты вершины .

38. Найти центр масс четырёхугольной однородной пластины с вершинами (−2; 1), (3; 6), (5; 2), (0; −6). Указание. Найти центры масс треугольников и и разделить расстояние между ними в отношении, обратном отношению площадей треугольников. Центр масс треугольника находится в точке пересечения его медиан.

39. Даны последовательные вершины однородной пятиугольной вершины: (2; 3), (0; 6), (−1; 5), (0; 1), (1; 1). Определить координа-

ты её центра масс.

40.Построить в полярной системе координат следующие точки:

1 (1; 4), 2 (3; 2), 3 (3; 56 ), 4(1,5; ), 5 (2√3; 43 ), 6 (4; − 3).

41. Определить полярные координаты точек, симметричных сточка-

ми 1 (1; 3), 2 (2; 23 ), 3 (13 ; − 6), 4(4; ), 5( ; ): 1) относительно полярной оси; 2) относительно полюса.

42.В полярной системе координат дана точка (8; 23 ). Найти

прямоугольные координаты этой точки при условии, что ось абсцисс совпадает с полярной осью, начало координат совпадает с полюсом.

43.В прямоугольной системе координат дана точка (−√2; −√2). Найти полярные координаты этой точки при условии, что ось абсцисс совпадает с полярной осью, начало координат совпадает с полюсом.

44.Вычислить расстояние между точками (5; 4) и (8; − 12), заданными в полярной системе координат.

56

45. В полярной системе даны две смежные вершины квадрата

(12; − 10) и (3; 15). Определить его площадь.

46.В полярной системе даны две противоположные вершины квадрата (6; − 712) и (4; 6). Определить его площадь.

47.Вычислить площадь треугольника, вершины которого (3; 8),

(8; 724), (6; 58 ) заданы в полярной системе координат.

48.Формулы преобразования координат заданы следующими равенствами: = ′ + 3, = ′ − 5. Определить старые координаты начала′ новой системы.

49.Написать формулы преобразования координат, если начало координат перенесено в точку ′(2; −4). Направление осей и масштаб сохранены.

50.Дана точка (−2; 5). Найти координаты этой точки в новой системе, если начало координат перенесено в точку ′(2; 1), направление осей и масштаб сохранены.

51.Начало координат перенесено в точку ′(−3; −4). Точка(−1; 4) определена в новой системе. Найти координаты этой точки в старой системе координат. Направление осей и масштаб сохранены.

52.Определить угол , на который повёрнуты оси, если формулы

преобразования координат заданы следующими равенствами: = √23 ′ −

−12 ′, = 12 ′ + √23 ′.

53.Написать формулы преобразования координат, если коорди-

натные оси повёрнуты на угол = 4 . Начало координат и масштаб сохранены.

54.Дана точка (3; 1). Найти координаты этой точки в новой системе, если оси координат повёрнуты на угол в −450, начало координат и масштаб сохранены.

55.Определить старые координаты нового начала координат и

угол , на который повёрнуты оси, если формулы преобразования коорди-

нат заданы следующими равенствами: = 12 ′ − √23 ′ − 4, = √23 ′ +

+ 12 ′ + 3.

56. Написать формулы преобразования координат, если коорди-

= 3 , начало координат перенесено в точку

′(5; −1). Масштаб сохранён.

57.Дана точка (12; −6). Найти координаты этой точки в новой системе, если начало координат перенесено в точку ′(2; −1), оси коорди-натные оси повёрнуты на угол

нат повёрнуты на угол = 34 , масштаб сохранён.

58. Начало координат перенесено в точку ′(−1;2), координатные оси повёрнуты на угол = 125 . Координаты точки (3; 2) определе-

57

ны в новой системе. Вычислить координаты этой точки в старой системе координат.

5.Даны три точки 1 площадь треугольника 1 2 3.

6.На плоскости даны три точки (−2; −1), (3; 2), (5; 6). Вы-)()()(

яснить, лежат ли они на одной прямой.

7.Написать формулы преобразования координат, если начало координат перенесено в точку ′(−5;7). Направление осей и масштаб сохранены.

8.Дана точка (3; −6). Найти координаты этой точки в новой системе, если начало координат перенесено в точку ′(−2; 1). Направление осей и масштаб сохранены.

9.Вычислить периметр треугольника по координатам его вершин

(−6; −5), (−3; −1) и (2; −13).

10.Даны две точки 1(−4; 9) и 2(−1; 3). Найти координаты

11.Даны вершины треугольника (−4; 3), (−1; −5), (6; 7). Определить длину его медианы, проведённой из вершины .

12.Построить в полярной системе координат следующие точки:

1 (3; 18), 2 (5; 2), 3 (1,8; 712), 4 (3√2; 3736 ), 5 (4; 53 ), 6(6; 2 ).

13. Написать формулы преобразования координат, если координатные оси повёрнуты на угол = 12 . Начало координат и масштаб сохранены.

14. Дана точка (3; −1). Найти координаты этой точки в новой системе, если оси координат повёрнуты на угол = √530 . Начало координат и масштаб сохранены.

58

Индивидуальные задания

Первый уровень сложности

1. Построение точек на плоскости в прямоугольной системе координат Задание 1. Построить точки на плоскости в прямоугольной системе

координат.

1.1.(−5; 6), (4; 1), (−2; −7), (6; −3), (0; 3), (−6; 0),

(−7,8; 4,2), (2; −√7).

1.2.(−1; −2), (−3; 4), (5; −8), (2; 3), (−6; 0), (0; 5),

(4,2; 5,6), (−9; √10).

1.3.(2; −4), (−5; 7), (5; 3), (−7; −8), (0; −6), (7; 0),

(−2,8; 1,6), (9,5; 4).

1.4.(7; −6), (−2; 1), (−3; −4), (8; 1), (0; −5), (3; 0),

(3,5; 4,2), (−6; −√3).

1.5.(1; 2), (−5; −4), (4; −3), (−5; 2), (8; 0), (0; −6),

(−7,4; −1,5), (2√10; 5).

1.6.(2; −3), (5; 6), (−6; 1), (−2; −5), (0; −4), (7; 0),

(3,7; 3,1), (4; −5,6).

1.7.(−1; −1), (3; 9), (2; −8), (−5; 1), (0; 9), (−4; 0),

(−6,4; 3,3), (8; √5 + 3).

1.8.(−3; 2), (5; −8), (4; 2), (−5; −6), (−8; 0), (0; −3),

(2,3; 5,9), (5 + √3; −2).

1.9.(5; 9), (−4; 1), (2; −5), (−2; −2), (0; 4), (7; 0),

(3,2; −7,6), (−√37; 5).

1.10.(6; 6), (−2; −4), (−5; 6), (3; −2), (0; 3), (−4; 0),

(8,2; −5,1), (√15; −1).

1.11.(−2; 4), (5; 3), (−6; −4), (1; −2), (3; 0), (0; 7),

(7,9; −6,5), (−√61; 5).

1.12.(4; −3), (7; 2), (−1; 8), (−4; −5), (0; 4), (−7; 0),

(−2,7; 6,1), (√5 + 1; −2).

1.13.(5; 1), (−3; 4), (2; −7), (−1; −2), (−4; 0), (0; 6),

(3,9; −4,5), (5√3; −1).

1.14.(3; −3), (−8; −5), (2; 6), (−1; 2), (0; 3), (7; 0),

(5,2; −7,4), (−√7; −4).

1.15.(−2; −1), (5; 4), (−5; 9), (7; −3), (0; 7), (−4; 0),

(−8,9; 6,4), (√2; −3).

1.16.(5; −7), (−3; 2), (−4; −4), (1; 2), (−6; 0), (0; −1),

(2,8; −5,2), (√5; −9).

1.17.(−6; −2), (−3; 2), (4; 4), (1; −5), (0; 3), (−1; 0),

(6,4; −7,2), (6√3; 6).

1.18.(3; −8), (9; 2), (−4; 3), (−4; −5), (5; 0), (0; −2),

59

(7,3; 5,6), (− √230 ; 5).

1.19.(6; −2), (−3; −4), (3; 8), (−1; 5), (0; −6), (1; 0),

(8,2; −9,3), (−2√5; 5).

1.20.(5; 1), (−6; −3), (2; −7), (−1; 2), (0; 6), (1; 0),

(−3,2; 4,5), (3√6; 8).

1.21.(3; 2), (−9; 5), (9; −5), (−4; −3), (−6; 0), (0; 7),

(5,6; −7,2), (−√2; 1).

1.22.(7; −2), (3; 8), (−4; 1), (−6; −3), (0; 5), (1; 0),

(5,3; −6,7), (−2√2; −5).

1.23.(9; 8), (−2; −2), (6; −1), (−5; 4), (0; −4), (−7; 0),

(2,4; 6,3), (6√3; 1).

1.24.(−4; 2), (3; −5), (6; 2), (−7; −8), (1; 0), (0; 5),

(−5,2; 7,8), (4√6; −4).

1.25.(−3; −5), (7; −8), (−1; 2), (5; 4), (0; 9), (−6; 0),

(2,3; −3,4), (4√7; 2).

1.26.(5; 2), (−3; 2), (4; −6), (−7; −1), (0; −4), (2; 0),

(−5,3; 7,8), (4√5; −4).

1.27.(5; 3), (−2; 1), (−4; −6), (3; −7), (−6; 0), (−0; 5),

(6,5; −2,8), (√3; 7).

1.28.(4; 3), (−9; 2), (7; −1), (−5; −4), (0; 3), (−1; 0),

(−2,9; 5,4), (5√5; −6).

1.29.(3; 5), (−2; 1), (8; −4), (−7; −6), (0; −1), (5; 0),

(−5,2; 7,4), (2√10; 3).

1.30.(7; 2), (1; −3), (−5; −3), (−4; 5), (0; −6), (1; 0),

(3,6; −7,7), (√23; 3).

1.31.(8; −2), (−3; 1), (−7; −1), (3; 4), (6; 0), (0; −5),

(−5,7; −7,1), (√3; −6).

1.32.(4; 5), (2; −4), (−3; 1), (−6; −8), (−5; 0), (0; 3),

(6,2; −5,3), (2√15; 7).

1.33.(−5; 1), (4; −2), (3; 9), (−7; −3), (−7; 0), (0; 5),

(−2,4; 7,5), (5√2; 3).

1.34.(3; 1), (−5; −2), (−6; 4), (3; −8), (7; 0), (0; −4),

(5,4; 6,1), (−4√6; −4).

1.35.(−2; −4), (−3; 9), (5; −7), (3; 2), (0; −1), (1; 0),

(−6,7; 5,8), (−4√5; −6).

1.36.(7; −2), (3; 1), (−8; 7), (−1; −4), (5; 0), (0; 5),

(−4,7; 3,9), (5√3; −6).

2. Расстояние между двумя точками на плоскости Задание 2. Найти расстояние между точками и на плоскости.