
659
.pdf
|
|
|
1 |
|
10 |
= |
2 |
|
5
−5 |
−2,5 |
|
Рис. 3.30. Отрезок прямой = , заключённый между прямыми
2 − + 5 = 0 и 2 − + 10 = 0 (к Примеру 3.20)
2 1 − 1 + 10 = 0, 2 2 − 2 + 5 = 0,
( 2 − 1)2 + ( 2 − 1)2 = 10,1 = 1,
{2 = 2.
В системе пять неизвестных: 1, 1, 2, 2, .
Решим систему. Вычтем из 5-ого уравнения 4-ое:
2 − 1 = ( 2 − 1).
Подставим результат в 3-е уравнение:
( 2 − 1)2 + 2( 2 − 1)2 = 10.
Преобразуем:
(1 + 2)( 2 − 1)2 = 10.
Далее вычтем из 1-ого уравнения 2-ое:
2( 1 − 2) − 1 + 2 + 5 = 0.
Преобразуем:
2 − 1 = −5 + 2( 2 − 1).
Приравняем полученные результаты для 2 − 1:
( 2 − 1) = −5 + 2( 2 − 1).
Преобразуем:
( 2 − 1)( − 2) = −5
2 − 1 = − −25 .
101

Подставим полученный результат в уравнение (1 + 2)( 2 − 1)2 =
10.
Получаем:
(1 + 2) ( 25 )2 = 10.
−2
Преобразуем:
5(1 + 2) = 2( − 2)2 5 + 5 2 = 2 2 − 8 + 8 3 2 + 8 − 3 = 0.
Корни уравнения: = −3 и = 13 .
Уравнения искомой прямой: = −3 и = 13 .
Преобразуем к общему уравнению прямой:
3 + = 0 и − 3 = 0. Ответ: 3 + = 0, − 3 = 0.
Пример. 3.21. Доказать, что через точку (−3; −1) можно провести бесконечно много прямых, отрезок каждой из которых, заключённый между прямыми − 2 + 5 = 0 и − 2 − 3 = 0, делится в точке пополам.
Решение. Рассмотрим одну из всевозможных прямых. Обозначим её через . Данные прямые обозначим через 1 и 2 соответственно. Точки пересечения прямой с данными прямыми обозначим через ( 1; 1) и( 2; 2) соответственно (рис. 3.31).
|
1 |
|
|
|
|
|
2,5 |
2 |
|
|
|
|
|
|
|
|
|
−5 |
3 |
|
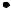
−1,5
Рис. 3.31. Отрезок произвольной прямой , заключённый между прямыми
− 2 + 5 = 0 и − 2 − 3 = 0 (к Примеру 3.21)
Так как точка лежит на прямой 1, то её координаты удовлетворяют уравнению этой прямой. Можно записать: 1 − 2 1 + 5 = 0. Так как точкалежит на прямой 2, то её координаты удовлетворяют уравнению этой прямой. Можно записать: 2 − 2 2 − 3 = 0.
Так как точка – середина отрезка ̅̅̅̅, то, применяя формулы
нахождения координат середины отрезка, получаем:
1+2 2 = −3, 1+2 2 = −1.
102
Преобразуем:
1 + 2 = −6, 1 + 2 = −2.
Полученные уравнения объединим в систему:
1 − 2 1 = −5,
{ 2 − 2 2 = 3,1 + 2 = −6,
1 + 2 = −2.
Получили систему линейных алгебраических уравнений относительно неизвестных 1, 2, 1, 2. Решим систему методом Гаусса.
Запишем расширенную матрицу системы:
1 0 −2 0 −5
(0 |
1 |
0 |
−2| 3 ). |
|
1 |
1 |
0 |
0 |
−6 |
0 |
0 |
1 |
1 |
−2 |
Приведём расширенную матрицу системы к ступенчатому виду. Прибавим к третьей строке первую, умноженную на −1:
1 |
0 |
−2 |
0 −5 |
|
(0 |
1 |
0 |
−2| 3 ). |
|
0 |
1 |
2 |
0 |
−1 |
0 |
0 |
1 |
1 |
−2 |
Прибавим к третьей строке вторую, умноженную на −1: |
||||
1 |
0 |
−2 |
0 −5 |
|
(0 |
1 |
0 |
−2| 3 ). |
|
0 |
0 |
2 |
2 |
−4 |
0 |
0 |
1 |
1 |
−2 |
Прибавим к третьей строке четвёртую, умноженную на −2:
1 |
0 |
−2 |
0 −5 |
|
(0 |
1 |
0 |
−2| 3 ). |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
−2 |
Вычеркнем нулевую строку:
1 |
0 |
−2 |
0 −5 |
|
(0 |
1 |
0 |
−2| 3 ). |
|
0 |
0 |
1 |
1 |
−2 |
Расширенная матрица системы приведена к ступенчатому виду. Ранг расширенной матрицы системы совпадает с рангом матрицы системы и равен 3. Следовательно, по теореме Кронекера–Капелли система совместна. Число неизвестных равно 4. Так как ранг меньше числа неизвестных, то система имеет бесконечное множество решений. Этим доказано, что через точку можно провести бесконечное множество прямых, отрезок каждой из которых, заключённый между прямыми − 2 + 5 = 0 и − 2 − 3 = = 0, делится в точке пополам.
Пример. 3.22. Площадь треугольника равна 8. Две его вершины – точки (1; −2) и (2; 3). Третья вершина лежит на прямой 2 + − 2 = = 0. Определить координаты вершины .
103
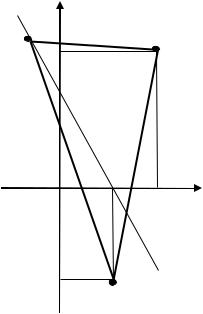
Решение. Данную прямую обозначим через . Сделаем чертёж (рис. 3.32). Обозначим координаты точки : ( 0; 0). Так как точка ле-
жит на прямой , то её координаты удовлетворяют уравнению этой прямой.
Можно записать: 2 0 + 0 − 2 = 0. Выразим 0: 0 = 2 − 2 0. Тогда координаты точки : ( 0; 2 − 2 0).
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 3.32. Треугольник (к Примеру 3.22) |
|||||||||||||||
Далее воспользуемся формулой для нахождения площади треуголь- |
|||||||||||||||||||
ника через координаты его вершин: ± = |
1 |
| 2 |
− 1 |
2 |
− 1|. |
||||||||||||||
|
− |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
− |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
1 |
Здесь 1 = 1, 1 = −2, 2 = 2, 2 = 3, 3 = 0, 3 |
= 2 − 2 0. |
||||||||||||||||||
Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
2 − 1 |
3 + 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
±8 = |
|
| 0 − 1 |
2 − 2 0 + 2|. |
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|||||||||||||
Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
±8 = |
|
| 0 − 1 |
4 − 2 0| |
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
±16 = 4 − 2 0 − 5 0 + 5 |
|
|
|
|
|
|
|
|
|
|
|||||||||
±16 = 9 − 7 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9 − 7 0 = 16 или 9 − 7 0 = −16 |
|
|
|
|
|
|
|||||||||||||
−7 0 = 7 или −7 0 = −25. |
|
|
|
|
|
|
|||||||||||||
Отсюда = −1, = |
25 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
|
0 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При 0 = −1 получаем 0 |
= 4. |
|
|
|
|
|
|
|
|||||||||||
При |
= |
25 |
получаем = − |
36 |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
0 |
7 |
|
|
|
0 |
|
7 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: (−1; 4), ( |
25 |
; − |
36 |
). |
|
|
|
|
|
|
|
|
|||||||
|
7 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. 3.23. Определить, при каких значениях прямая ( + 2) + +( 2 − 9) + 3 2 − 8 + 5 = 0:
1)параллельна оси абсцисс;
2)параллельна оси ординат;
104

3)проходит через начало координат.
Вкаждом случае записать уравнение прямой.
Решение. Прямая задана общим уравнением + + = 0.
В 1) прямая параллельна оси абсцисс, поэтому = 0. Отсюда полу-
чаем: + 2 = 0 и = −2.
Подставим в исходное уравнение = −2:
(−2 + 2) + ((−2)2 − 9) + 3 ∙ (−2)2 − 8 ∙ (−2) + 5 = 0.
Получаем следующее уравнение прямой: −5 + 33 = 0, 5 − 33 = 0.
В 2) прямая параллельна оси ординат, поэтому = 0. Отсюда полу-
чаем: 2 − 9 = 0 и = ±3.
Подставим в исходное уравнение = 3:
(3 + 2) + (32 − 9) + 3 ∙ 32 − 8 ∙ 3 + 5 = 0.
Получаем следующее уравнение прямой: 5 + 8 = 0.
Подставим в исходное уравнение = −3:
(−3 + 2) + ((−3)2 − 9) + 3 ∙ (−3)2 − 8 ∙ (−3) + 5 = 0.
Получаем следующее уравнение прямой: − 56 = 0.
В 3) прямая проходит через начало координат, поэтому = 0. Отсю-
да получаем: 3 2 − 8 + 5 и = 1, = 53 .
Подставим в исходное уравнение = 1:
(1 + 2) + (12 − 9) + 3 ∙ 12 − 8 ∙ 1 + 5 = 0.
Получаем следующее уравнение прямой: 3 − 8 = 0. Подставим в исходное уравнение = 53:
(53 + 2) + ((53)2 − 9) + 3 ∙ (53)2 − 8 ∙ (53) + 5 = 0.
Преобразуем:
113 − 569 = 0.
Получаем следующее уравнение прямой: 33 − 56 = 0.
Ответ: 1) = −2, 5 − 33 = 0; 2) = 3, 5 + 8 = 0; = −3, − 56 = 0; 3) = 1, 3 − 8 = 0; = 53 , 33 − 56 = 0.
3.6. Уравнение прямой в отрезках
Пусть задана прямая . Возьмём её общее уравнение + + = = 0, ≠ 0, ≠ 0, ≠ 0. Выполним преобразования.
Перенесём слагемое в правую часть:
+ = − .
Разделим уравнение на – ( ≠ 0):
−С + −С = 1.
Дробь не изменится, если числитель и знаменатель разделить на одно и то же число, не равное нулю. Разделим числитель и знаменатель первой дроби на ( ≠ 0), разделим числитель и знаменатель второй дроби на
( ≠ 0):
С + С = 1.
− −
105
Обозначим − С через , − С обозначим через . Уравнение принимает
вид:
+ = 1.
Полученное уравнение называется уравнением прямой в отрезках.
Выясним смысл величин и . Возьмём = 0. Получаем: |
|
= 1. От- |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сюда = . Прямая проходит через точку (0; ), то есть отсекает на оси |
|||||||||||||||||||||||||||||||
отрезок величины . Возьмём = 0. Получаем: |
|
= 1. |
Отсюда = . |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Прямая проходит через точку ( ; 0), то есть отсекает на оси отрезок |
|||||||||||||||||||||||||||||||
величины . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, и – это величины отрезков, которые прямая отсе- |
|||||||||||||||||||||||||||||||
кает на осях координат (рис. 3.33). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Рис. 3.33. Геометрический смысл величин и |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
в уравнении прямой |
|
+ |
|
= 1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. 3.24. Среди приведённых уравнений указать уравнения |
|||||||||||||||||||||||||||||||
прямой в отрезках: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) |
|
+ |
|
= 1; |
2) − = 0; |
3) = − 4; |
|
|
|
|
|
||||||||||||||||||||
2 |
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
|
|
+ |
|
= 1; |
5) = 0; |
6) 3 2 − 2 2 − 1 = 0; |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
−4 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
7) + |
|
= 1; |
8) |
|
+ |
|
|
= 0; |
9) 2 2 − = 0; |
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
− |
2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10) 2 |
|
+ 2 = 3; |
11) = |
+ 3; |
12) 3 − 4 = 0. |
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Уравнение прямой в отрезках имеет вид |
+ |
= 1. Среди |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
приведённых уравнений такому виду соответствуют уравнения под номе-
рами 1), 4), 7).
Ответ: 1), 4), 7).
Пример. 3.25. Преобразовать данные уравнения к уравнению прямой
в отрезках и построить эти прямые: |
|
|
|
|
||
1) 3 + 2 − 6 = 0; |
2) 4 − 6 − 5 = 0; |
|
|
|
|
|
3) = 2 + 1; |
4) − 2 = 0. |
|
|
|
|
|
Решение. Преобразуем данные уравнения к виду |
+ |
= 1. |
||||
|
|
|||||
|
|
|
|
|||
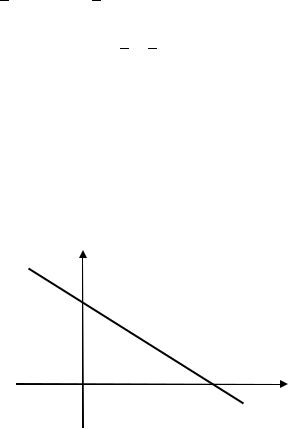
1) 3 + 2 − 6 = 0.
Прямая задана общим уравнением. Перенесём числовое слагаемое в правую часть:
106
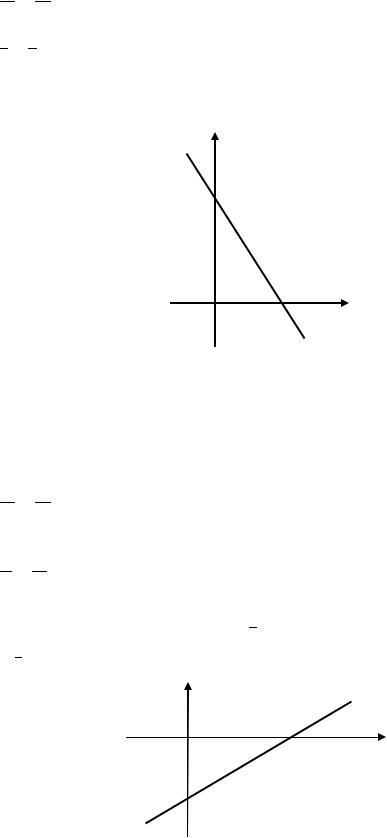
3 + 2 = 6.
Затем разделим уравнение на 6:
36 + 26 = 1.
Преобразуем:
2 + 3 = 1.
Получили уравнение прямой в отрезках. На оси абсцисс прямая отсекает отрезок, величина которого равна 2, на оси ординат величина отрезка равна 3 (рис. 3.34).
3
|
2 |
|
|
|
|
Рис. 3.34. Прямая, заданная уравнением |
|
+ |
|
= 1 (к Примеру 3.25) |
|
2 |
|
||||
|
|
3 |
|
||
2) 4 − 7 − 5 = 0.
Прямая задана общим уравнением. Перенесём числовое слагаемое в правую часть:
4 − 7 = 5.
Затем разделим уравнение на 5:
45 − 75 = 1.
Разделим числитель и знаменатель первой дроби на 4, второй дроби
– на 7 и уберём "минус" перед второй дробью в знаменатель. Получаем:
5 + −5 = 1.
4 7
Получили уравнение прямой в отрезках. На оси абсцисс прямая отсекает отрезок, величина которого равна 54 , на оси ординат величина отрезка равна − 57 (рис. 3.35).
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
− |
5 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.35. Прямая, заданная уравнением |
|
+ |
|
= 1 (к Примеру 3.25) |
|||||
5 |
5 |
||||||||
|
4 |
|
− |
7 |
|||||
|
|
|
|||||||
|
107 |
|
|
|
|
|
|
|
|

3) = 2 + 1.
Прямая задана уравнением с угловым коэффициентом. Перенесём слагаемое, содержащее переменную , в левую часть:
−2 + = 1.
Преобразуем первое слагаемое:
−2 = − |
2 |
= |
2 |
|
= |
|
. |
|
|
|
1 |
||||||
|
1 −1 |
|
− |
2 |
||||
|
|
|
|
|
|
|
||
Получаем:
1 + = 1.
−2 1
Получили уравнение прямой в отрезках. На оси абсцисс прямая отсекает отрезок, величина которого равна − 12 , на оси ординат величина отрезка равна 1 (рис. 3.36).
1
− |
1 |
|
|
|
|
|
||
|
|
|
|
|
||||
2 |
|
|
|
|||||
|
|
|
|
|
|
|||
Рис. 3.36. Прямая, заданная уравнением |
|
+ |
|
= 1 (к Примеру 3.25) |
||||
1 |
|
|||||||
|
|
|
|
− |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
4) − 2 = 0. Прямая задана общим уравнением, причём уравнение
неполное, в нём отсутствует слагаемое . Поэтому прямая проходит через начало координат и данное уравнение невозможно преобразовать к уравнению прямой в отрезках.
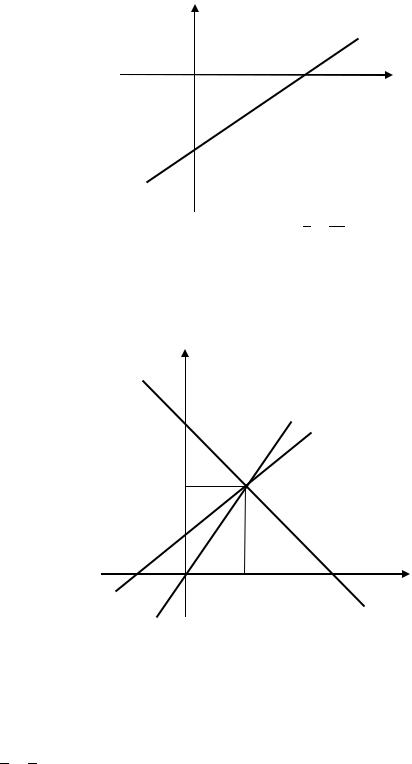
Пример. 3.26. Вычислить площадь треугольника, отсекаемого прямой 3 − 4 − 12 = 0 от координатного угла.
Решение. Приведём данное уравнение прямой к уравнению прямой в отрезках. Перенесём числовое слагаемое в правую часть:
3 − 4 = 12.
Разделим уравнение на 12:
4 − 3 = 1.
Минус перед вторым слагаемым уберём в знаменатель:
4 + −3 = 1.
Получили уравнение прямой в отрезках. На оси абсцисс прямая отсекает отрезок, величина которого равна 4, на оси ординат величина отрезка равна −3 (рис. 3.37). Получили прямоугольный треугольник , катеты
которого равны 3 и 4. Площадь треугольника :
= 12 | | ∙ | | = 12 ∙ 4 ∙ 3 = 6.
108
|
4 |
|
|
−3
Рис. 3.37. Прямая, заданная уравнением 4 + −3 = 1 (к Примеру 3.26)
Ответ: 6.
Пример. 3.27. Составить уравнение прямой, которая проходит через точку (2; 3) и отсекает на координатных осях отрезки равной длины, считая каждый отрезок от начала координат.
Решение. Возможны три варианта расположения прямой (рис. 3.38).
(1) |
|
|
|
|
|
|
1 |
(3) |
|
|
(2) |
|
3 |
|
|
2 |
|
2 |
|
1 |
|
2 |
|
Рис. 3.38. Прямая, проходящая через точку (2; 3) и отсекающая на координатных осях отрезки равной длины (к Примеру 3.27)
1) В первом варианте, на чертеже прямая (1), величины отрезков, отсекаемых прямой на осях координат, равны, то есть 1 = 1. Обозначим длины этих отрезков через , тогда уравнение прямой можно записать в ви-
де:
+ = 1.
Преобразуем:
+ = .
Так как прямая проходит через точку (2; 3), то координаты этой точки удовлетворяют уравнению прямой. Подставим координаты точки в уравнение прямой:
2 + 3 = .
Отсюда = 5 и уравнение прямой принимает вид + − 5 = 0.
109
2) Во втором варианте, на чертеже прямая (2), величины отрезков, отсекаемых прямой на осях координат, отличаются знаком, то есть 2 = = − 2. Обозначим длины этих отрезков через , тогда уравнение прямой
можно записать в виде:
− + = 1.
Преобразуем:
− = − .
Так как прямая проходит через точку (2; 3), то координаты этой точки удовлетворяют уравнению прямой. Подставим координаты точки в уравнение прямой:
2 − 3 = − .
Отсюда = 1 и уравнение прямой принимает вид − + 1 = 0.
3) В третьем варианте, на чертеже прямая (3), величины отрезков, отсекаемых прямой на осях координат, равны нулю, то есть прямая проходит через начало координат и уравнение прямой можно записать в виде = ,
где = 32 . Получаем = 32 . После преобразований: 3 − 2 = 0.
Ответ: + − 5 = 0, − + 1 = 0, 3 − 2 = 0.
3.7. Нормальное уравнение прямой
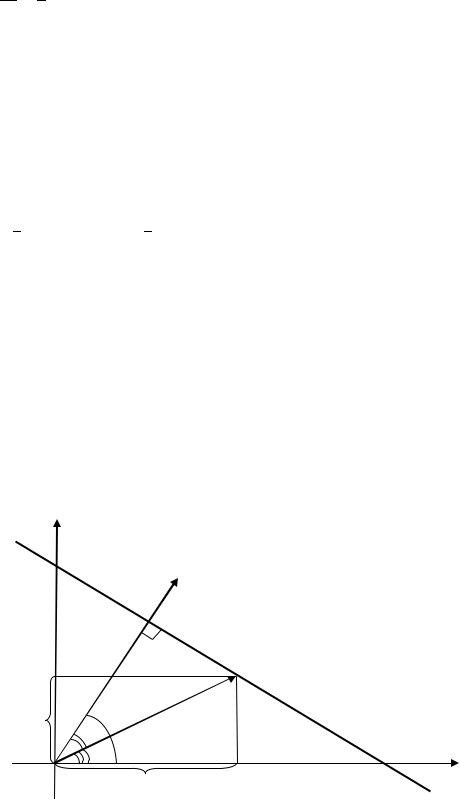
Пусть задана прямая . Проведём через начало координат прямую перпендикулярно прямой . Прямую называют нормалью. Обозначим через точку пересечения нормали с данной прямой. На нормали зададим положительное направление от начала координат к точке . Обозначим через угол наклона нормали к оси , через длину отрезка ̅̅̅̅.
Пусть ( ; ) – произвольная точка прямой. Обозначим через
проекцию точки на ось , через – проекцию точки на ось .
Обозначим через угол наклона отрезка ̅̅̅̅̅ к оси , через – угол наклона нормали к отрезку ̅̅̅̅̅ (рис. 3.39).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Θ |
|
|
|
|
|
|
|
|
|
|
Рис. 3.39. Нормальное уравнение прямой
110
