
659
.pdf
Пример. 3.35. Дана прямая 7 + 2 − 5 = 0. Определить угловой коэффициент прямой: а) параллельной данной прямой; б) перпендикулярной данной прямой.
Решение. Данная прямая задана общим уравнением. Преобразуем его к уравнению прямой с угловым коэффициентом, то есть к виду = = + , где – угловой коэффициент прямой:
2 = −7 + 5,
= − |
7 |
|
+ |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
||||||
Угловой коэффициент прямой = − |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
а) Угловые коэффициенты параллельных прямых равны, поэтому уг- |
||||||||||||||||||||||||||||||||||||||||
ловой коэффициент искомой прямой также равен − |
7 |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
б) Угловые коэффициенты перпендикулярных прямых связаны ра- |
||||||||||||||||||||||||||||||||||||||||
венством ′ = − |
1 |
|
|
|
, где ′ – угловой коэффициент искомой прямой, – уг- |
|||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
ловой коэффициент данной прямой. Отсюда ′ = − |
1 |
= − |
1 |
= |
2 |
. |
||||||||||||||||||||||||||||||||||
|
7 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
7 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: а) − |
|
; б) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. 3.36. Среди заданных пар прямых найти параллельные: |
||||||||||||||||||||||||||||||||||||||||
1) = −2 + 8, = 2 + 8; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2) = − + 2, = − − 2; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
3) 5 − + 1 = 0, 10 − 2 − 7 = 0; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
4) = |
3 |
+ |
1 |
, 6 − 8 − 3 = 0; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5) 3 − 4 + 1 = 0, 5 + 3 − 4 = 0; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
6) |
|
|
+ |
|
|
= 1, 2 − 4 + 7 = 0; |
|
|
|
|
|
|
||||||||||||||||||||||||||||
−3 |
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7) = − |
− 2; |
+ |
= 1; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
12 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
8) |
|
|
+ |
|
= 1, |
|
+ |
|
|
= 1. |
|
|
|
|
|
|
||||||||||||||||||||||||
−5 |
5 |
1 |
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Решение.
1)= −2 + 8, = 2 + 8. Обе прямые заданы уравнением прямой
сугловым коэффициентом. Условием их параллельности является равен-
ство угловых коэффициентов. Угловой коэффициент первой прямой 1 = −2, угловой коэффициент второй прямой 2 = 2. Угловые коэффициенты не равны, поэтому прямые не параллельны.
2) = − + 2, = − − 2. Обе прямые заданы уравнением прямой с угловым коэффициентом. Условием их параллельности является равенство угловых коэффициентов. Угловой коэффициент первой прямой 1 = −1, угловой коэффициент второй прямой 2 = −1. Угловые коэффициенты равны, поэтому прямые параллельны.
3) 5 − + 1 = 0, 10 − 2 − 7 = 0. Обе прямые заданы общим уравнением. Условием их параллельности является пропорциональность
коэффициентов при неизвестных, то есть 1 = 1 . В условиях нашего при-
2 2
121

мера: 1 = 5, 2 = 10, 1 = −1, 2 = −2. Составим пропорцию: 105 = −1−2 . Отсюда: 12 = 12 . Пропорция верная, поэтому прямые параллельны.
4) = 34 + 14 , 6 − 8 − 3 = 0. Первая прямая задана уравнением с
угловым коэффициентом, вторая прямая задана общим уравнением. Преобразуем уравнение второй прямой к уравнению прямой с угловым коэффи-
циентом: = 34 − 38 . Угловой коэффициент первой прямой 1 = 34 , угловой коэффициент второй прямой 2 = 34 . Угловые коэффициенты обеих
прямых равны, поэтому прямые параллельны.
5) 3 − 4 + 1 = 0, 5 + 3 − 4 = 0. Обе прямые заданы общим уравнением. Условием их параллельности является пропорциональность
коэффициентов при неизвестных. Составим пропорцию: 35 = −34 . Пропорция неверная, поэтому прямые не параллельны.
6) |
|
|
+ |
|
= 1, 2 − 4 + 7 = 0. Первая прямая задана уравнением |
−3 |
3 |
||||
|
2 |
|
|||
|
|
|
|
||
прямой в отрезках, вторая прямая задана общим уравнением прямой. Пре-
образуем уравнение первой прямой к общему уравнению:
− 3 + 23 − 1 = 0,− 2 + 3 = 0.
Проверим пропорциональность коэффициентов при неизвестных:
12 = −2−4 . Отсюда: 12 = 12 . Коэффициенты при неизвестных пропорциональны, поэтому прямые параллельны.
7) = − 13 − 2; 12 + 4 = 1. Первая прямая задана уравнением пря-
мой с угловым коэффициентом, вторая прямая задана уравнением прямой в отрезках. Преобразуем уравнение второй прямой к уравнению прямой с угловым коэффициентом:
|
|
= − |
|
|
|
+ 1, |
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= − |
1 |
|
+ 4. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
Угловой коэффициент первой прямой = − |
|
, угловой коэффици- |
|||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
ент второй прямой 2 = − |
. Угловые коэффициенты обеих прямых равны, |
|||||||||||||||||||
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поэтому прямые параллельны. |
|
|
|
|||||||||||||||||
8) |
|
+ |
|
= 1, |
|
+ |
|
|
= 1. Обе прямые заданы уравнением прямой в |
|||||||||||
|
5 |
1 |
1 |
|
||||||||||||||||
|
|
|
−5 |
4 |
|
3 |
5 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отрезках. Приведём уравнения обеих прямых, например, к уравнению прямой с угловым коэффициентом.
Преобразуем первое уравнение:
5 = 5 + 1,
4
= 14 + 54 .
Преобразуем второе уравнение:
1 = − 1 + 1,
5 3
122

= − |
3 |
+ |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
Угловой коэффициент первой прямой = |
|
, угловой коэффициент |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
второй прямой 2 |
= − |
|
|
. Угловые коэффициенты не равны, поэтому пря- |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||
мые не параллельны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ответ: 2, 3, 4, 6, 7. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Пример. 3.37. Среди заданных пар прямых найти перпендикулярные: |
|||||||||||||||||||||||||||||
1) 2 − + 3 = 0, + 2 − 4 = 0; |
|
|
|
||||||||||||||||||||||||||
2) = − |
1 |
+ 1, = −2 + 1; |
|
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) 5 + 4 + 1 = 0, = −3 − 4; |
|
|
|
||||||||||||||||||||||||||
4) = −8 + 6, = |
1 |
+ 1; |
|
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|||||
5) |
|
+ |
|
= 1, |
|
+ |
|
= 1; |
|
|
|
||||||||||||||||||
1 |
1 |
1 |
2 |
|
|
|
|||||||||||||||||||||||
|
− |
3 |
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6) 5 + 2 − 7 = 0, − − 4 = 0; |
|
|
|
||||||||||||||||||||||||||
7) = 2 − 1; |
|
+ |
|
= 1; |
|
|
|
||||||||||||||||||||||
3 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
|
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8) |
+ = 1, + 3 − 8 = 0. |
|
|
|
|||||||||||||||||||||||||
1 |
|
|
|
||||||||||||||||||||||||||
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) 2 − + 3 = 0, |
+ 2 − 4 = 0. Обе прямые заданы общим урав- |
||||||||||||||||||||||||||||
нением. Условием их перпендикулярности является равенство 1 2 + + 1 2 = 0, где 1 и 2 – коэффициенты при переменной в общем уравнении прямой, 1 и 2 – коэффициенты при переменной в общем уравнении прямой. В условиях нашего примера: 1 = 2, 2 = 1, 1 = −1, 2 = 2. Проверяем равенство: 2 ∙ 1 + (−1) ∙ 2 = 0. Отсюда: 0 = 0. Равенство верное, поэтому прямые перпендикулярны.
2) = − 12 + 1, = −2 + 1. Обе прямые заданы уравнением прямой с угловым коэффициентом. Условием их перпендикулярности является равенство 1 ∙ 2 = −1. Угловой коэффициент первой прямой 1 = − 12 , угловой коэффициент второй прямой 2 = −2. Проверяем равенство:
− 12 ∙ (−2) = −1. Отсюда 1 ≠ −1. Равенство неверное, поэтому прямые не
перпендикулярны.
3) 5 + 4 + 1 = 0, = −3 − 4. Первая прямая задана общим уравнением, вторая прямая задана уравнением прямой с угловым коэффициентом. Преобразуем уравнение второй прямой к общему уравнению прямой:
3 + + 4 = 0. Проверим равенство 1 2 + 1 2 = 0: 5 ∙ 3 + 4 ∙ 1 = 0. От-
сюда 19 ≠ 0. Равенство неверное, поэтому прямые не перпендикулярны.
4)= −8 + 6, = 18 + 1. Обе прямые заданы уравнением прямой
сугловым коэффициентом. Угловой коэффициент первой прямой 1 = −8 , угловой коэффициент второй прямой 2 = 18 . Проверяем равенство
=−1: −8 ∙ 1 = −1. Отсюда −1 = −1. Равенство верное, поэтому1 ∙ 2
8
прямые перпендикулярны.
123
5) |
|
+ |
|
= 1, |
|
+ |
|
= 1. Обе прямые заданы уравнением прямой в |
|
1 |
1 |
1 |
2 |
||||||
|
− |
3 |
4 |
|
2 |
3 |
|
||
|
|
|
|
||||||
отрезках. Приведём уравнения обеих прямых, например, к общему уравнению прямой.
Преобразуем первое уравнение:
−3 + 4 − 1 = 0; 3 − 4 + 1 = 0.
Преобразуем второе уравнение:
2 + 32 − 1 = 0; 4 + 3 − 2 = 0.
Проверим равенство 1 2 + 1 2 = 0: 3 ∙ 4 + (−4) ∙ 3 = 0. Отсюда 0 = 0. Равенство верное, поэтому прямые перпендикулярны.
6) 5 + 2 − 7 = 0, − − 4 = 0. Обе прямые заданы общим урав-
нением. Проверим равенство 1 2 + 1 2 = 0: 5 ∙ 1 + 2 ∙ (−1) = 0. Отсюда: 3 = 0. Равенство неверное, поэтому прямые не перпендикулярны.
7) = 2 − 1; 3 + = 1. Первая прямая задана уравнением прямой с
−2 3
угловым коэффициентом, вторая прямая задана уравнением прямой в отрезках. Преобразуем уравнение второй прямой к уравнению прямой с угловым коэффициентом:
= 1 − 3 ,
3 −2
= 3 + 2 ;
= 2 + 3.
Угловой коэффициент первой прямой 1 = 2 , угловой коэффициент второй прямой 2 = 2 . Проверяем равенство 1 ∙ 2 = −1: 2 ∙ 2 = −1. Отсюда 4 = −1. Равенство неверное, поэтому прямые не перпендикулярны.
8) |
|
|
+ = 1, |
+ 3 − 8 = 0. Первая прямая задана уравнением |
|
1 |
|||||
|
− |
3 |
|
|
|
|
|
|
|
||
прямой в отрезках, вторая прямая задана общим уравнением прямой. Преобразуем уравнение первой прямой к общему уравнению:
−3 + − 1 = 0; 3 − + 1 = 0.
Проверим равенство 1 2 + 1 2 = 0: 1 ∙ 3 + 3 ∙ (−1) = 0. Отсюда: 0 = 0. Равенство верное, поэтому прямые перпендикулярны.
Ответ: 1, 4, 5, 8.
Пример. 3.38. Составить уравнение прямой, проходящей через точку
(2; −1) параллельно прямой 4 − 7 + 12 = 0.
Решение. Обозначим через угловой коэффициент данной прямой, через 1 обозначим угловой коэффициент искомой прямой. Так как искомая и данная прямые параллельны, то их угловые коэффициенты равны:= 1. Найдём угловой коэффициент данной прямой. Данная прямая задана общим уравнением. Преобразуем его к уравнению прямой с угловым коэффициентом, то есть к виду = + , где – угловой коэффициент прямой:
7 = 4 + 12,
124

= 47 + 127 .
Таким образом, угловой коэффициент данной прямой = 47 и угловой коэффициент искомой прямой 1 = 47 .
Далее воспользуемся уравнением прямой с данным угловым коэффициентом и проходящей через данную точку: − 1 = 1( − 1), где ( 1; 1) – данная точка; в условиях примера – это точка (2; −1).
Подставляем данные:
− (−1) = 47 ( − 2), 7( + 1) = 4( − 2),
4 − 7 − 15 = 0. Ответ: 4 − 7 − 15 = 0.
Пример. 3.39. Составить уравнение прямой, проходящей через точку(−5; 2) перпендикулярно прямой 4 − + 3 = 0.
Решение. Обозначим через угловой коэффициент данной прямой, через 1 обозначим угловой коэффициент искомой прямой. Так как искомая и данная прямые перпендикулярны, то произведение их угловых коэф-
фициентов равно −1: 1 = −1. Отсюда 1 = − 1 . Найдём угловой коэф-
фициент данной прямой. Данная прямая задана общим уравнением. Преобразуем его к уравнению прямой с угловым коэффициентом, то есть к виду= + , где – угловой коэффициент прямой: = 4 + 3. Таким образом, угловой коэффициент данной прямой = 4 и угловой коэффициент
искомой прямой 1 = − 1 = − 14 .
Далее воспользуемся уравнением прямой с данным угловым коэффициентом и проходящей через данную точку: − 1 = 1( − 1), где ( 1; 1) – данная точка; в условиях примера – это точка (−5; 2).
Подставляем данные:
− 2 = − 14 ( − (−5)), 4( − 2) = −( + 5),
+ 4 − 3 = 0. Ответ: + 4 − 3 = 0.
Пример. 3.40. Даны середины сторон треугольника 1(2; 1),2(5; 3), 3(3; −4). Составить уравнения его сторон.
Решение. Сделаем схематичный чертёж (рис. 3.44).
Отрезок 1 2 является средней линией треугольника. Как известно из элементарной геометрии, средняя линия треугольника параллельна одной из его сторон, поэтому отрезок 1 2 параллелен стороне и значит
угловые коэффициенты прямых, содержащих отрезки 1 2 |
и , равны: |
||||||||||
|
= . |
|
|
|
|
|
|
||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Найдём угловой коэффициент отрезка 1 2: |
|
||||||||
|
|
|
= |
2− 1 |
= |
3−1 |
= |
2 |
. |
|
|
|
|
|
|
|
|
||||||
|
|
1 |
2 |
|
2− 1 |
|
5−2 3 |
|
|||
|
|
|
|
|
|
|
|||||
125
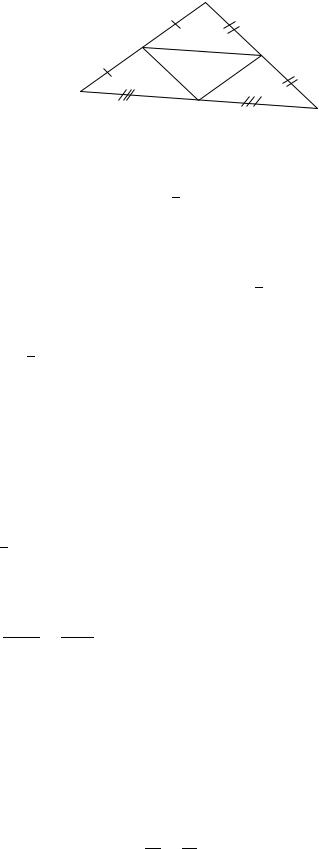
|
|
|
|
2 |
3 |
|
|
|
|
1 |
|
|
Рис. 3.44. Составление уравнений сторон треугольника по известным координатам середин сторон (к Примеру 3.40)
Таким образом, 1 2 = = 23 .
Далее можно составить уравнение стороны , используя уравнение прямой с данным угловым коэффициентом и проходящей через данную
точку: − 0 = ( − 0), где – угловой коэффициент прямой, ( 0; 0) – данная точка прямой. В условиях примера = 23 . Данная точка прямой –
это точка 3(3; −4). Подставляем данные в уравнение и преобразуем его
общему уравнению прямой:
− (−4) = 23 ( − 3), 3( + 4) = 2( − 3),
2 − 3 − 18 = 0.
Аналогично составляем уравнения остальных сторон треугольника. |
||||||||||||
Найдём угловой коэффициент отрезка 2 3: |
||||||||||||
|
= |
2− 1 |
= |
−4−3 |
= |
7 |
. |
|
|
|||
|
|
|
||||||||||
2 |
3 |
|
2− 1 |
|
3−5 |
2 |
|
|
||||
|
|
|
|
7 |
|
|||||||
Таким образом, |
|
|
= = |
. |
||||||||
2 3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
Составляем уравнение стороны2 :
− 1 = 72 ( − 2), 2( − 1) = 7( − 2),
7 − 2 − 12 = 0.
Найдём угловой коэффициент отрезка 1 3:
1 3 = 2− 1 = −4−1 = −5.2− 1 3−2
Таким образом, 1 3 = = −5 . Составляем уравнение стороны :
− 3 = −5( − 5), 5 + − 28 = 0.
Ответ: 2 − 3 − 18 = 0, 7 − 2 − 12 = 0, 5 + − 28 = 0.
3.10. Нахождение точки пересечения двух прямых на плоскости
Если прямые не параллельны, то есть для них не выполняется усло-
вие параллельности ( 1 ≠ 2 или 1 ≠ 1), то прямые пересекаются в неко-
2 2
торой точке.
126

Нахождение точки пересечения двух прямых на плоскости, когда прямые заданы уравнением с угловым коэффициентом
Пусть прямые 1 и 2 заданы уравнением с угловым коэффициентом:
= 1 + 1 и = 2 + 2.
Для нахождения координат точки пересечения прямых решим их
уравнения совместно, то есть составим систему уравнений:
{ = 1 + 1,= 2 + 2.
Решение системы будет являться общей точкой для обеих прямых. Так как левые части уравнений одинаковые, то можно приравнять правые части. Получаем уравнение:
1 + 1 = 2 + 2.
Решим уравнение относительно :
1 − 2 = 2 − 1;( 1 − 2) = 2 − 1;
= 2− 1 .1− 2
Затем полученное выражение подставим вместо в любое уравнение, например, в первое:
= |
2− 1 |
+ = 1 2− 1 1+ 1 1− 2 1 |
= 1 2− 2 1. |
||||||
1 |
|
− |
1 |
|
− |
|
|
− |
|
|
1 |
2 |
|
1 |
2 |
1 |
2 |
|
|
Получаем следующую точку пересечения прямых: ( 2− 1 ; 1 2− 2 1).
1− 2 1− 2
Нахождение точки пересечения двух прямых на плоскости, когда прямые заданы общим уравнением
Пусть прямые 1 и 2 заданы общим уравнением:
1 + 1 + 1 = 0 и 2 + 2 + 2 = 0, причём 12 + 12 ≠ 0,22 + 22 ≠ 0.
Для нахождения координат точки пересечения прямых решим их
уравнения совместно, то есть составим систему уравнений:
{ 1 + 1 + 1 = 0,2 + 2 + 2 = 0.
Перенесём числовые слагаемые в правые части:
{ 1 + 1 = −1,2 + 2 = −2.
Полученная система является системой линейных алгебраических уравнений относительно неизвестных и . Решим систему, например, по
правилу Крамера. |
|
|
|
|
|
|
|
|
|
|
|
||
Вычислим определитель системы: |
|
|
|
|
|
|
|||||||
∆= | 1 |
1| = − . |
|
|
|
|
|
|
|
|||||
2 |
2 |
1 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|||
Так прямые не параллельны, то |
≠ |
и отсюда − ≠ 0. |
|||||||||||
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
2 |
1 |
2 |
2 |
1 |
|
Таким образом ∆≠ 0 и система имеет единственное решение и следовательно прямые имеют единственную точку пересечения.
Далее найдём определители ∆1 и ∆2:
127
∆ = |− 1 |
|
1| = − + , ∆ |
= | 1 |
− 1| = − + . |
|||||||||||||||||||||||||
1 |
|
− 2 |
|
2 |
|
|
|
|
1 |
2 |
|
|
2 |
1 |
2 |
|
2 |
− 2 |
1 |
2 |
2 |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Найдём неизвестные и : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
∆1 |
= |
− 1 2+ 2 1 |
, = |
∆2 |
= |
− 1 2+ 2 1 |
. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
∆ |
|
|
|
− |
|
|
|
|
∆ |
|
− |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
2 |
|
1 |
|
|
|
|
|
|
1 |
2 |
2 |
1 |
|
|
|
|
|
|
|
Получаем следующую точку пересечения прямых: |
|
|
|
|
|||||||||||||||||||||||||
( |
− 1 2+ 2 1 |
; |
|
− 1 2+ 2 1 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
− |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
2 |
2 |
|
1 |
|
|
1 |
2 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При решении примеров возможна ситуация, когда выполняется усло-
вие параллельности прямых. Тогда нужно проверить условие совпадения прямых: 1 = 2, 1 = 2, когда прямые заданы уравнением прямой с угло-
вым коэффициентом, и 1 = 1 = 1 , когда прямые заданы общим уравне-
2 2 2
нием. Если прямые параллельны, то они не имеют общей точки. Если прямые совпадают, то они имеют бесконечно много общих точек.
Пример. 3.41. Найти точку пересечения двух прямых:
1)= − 23 − 73 , = − 56 − 53 ;
2)3 + 7 − 10 = 0, 5 + 2 − 36 = 0;
3)2 − + 8 = 0, 4 − 2 − 1 = 0;
4)− 3 + 2 = 0, 3 + − 5 = 0;
5)= −4 − 12 , = −4 + 2;
6)2 − 4 − 11 = 0, 4 − 8 − 22 = 0;
7)5 + 8 − 1 = 0, 4 − 3 + 18 = 0;
8)6 − 5 + 9 = 0, 4 − 3 = 0;
9)3 + 1 = 0, − 6 + 7 = 0;
10)= − 12 + 1, 7 + 14 + 6 = 0.
11)8 + 3 = 0, 5 − 2 = 0.
Решение.
1) = − 23 − 73 , = − 56 − 53 . Прямые заданы уравнением прямой с угловым коэффициентом. Угловые коэффициенты прямых не совпадают: − 23 ≠ − 56 , поэтому прямые не параллельны и, значит, пересекаются в неко-
торой точке. Найдём эту точку.
Приравниваем правые части уравнений:
− 23 − 73 = − 56 − 53 .
Найдём :
56 − 23 = 73 − 53 , 16 = 23 ,
= 4.
Найдём , подставив найденное значение , например, в уравнение
первой прямой:
= − 23 ∙ 4 − 73 = −5.
Таким образом, получаем следующую точку пересечения прямых:
(4; −5)
128

2) 3 + 7 − 10 = 0, 5 + 2 − 36 = 0. Прямые заданы общим уравнением. Коэффициенты при и не пропорциональны: 35 ≠ 72 , поэтому
прямые не параллельны и, значит, пересекаются в некоторой точке. Найдём эту точку.
Объединим уравнения прямых в систему:
|
|
|
3 + 7 − 10 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
{5 + 2 − 36 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Перепишем систему в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 + 7 = 10, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
{5 + 2 = 36. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Решим систему, например, по правилу Крамера: |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
∆= |3 7| = −29, |
|
|
∆ = |10 |
7| = −232, |
|
∆ |
2 |
= |3 |
10| = 58, |
|||||||||||||||||
|
|
|
|
5 |
2 |
|
|
|
1 |
|
36 |
2 |
|
|
|
|
5 |
36 |
|
|
||||||||
|
|
= |
∆1 |
= |
−232 |
= 8 , |
= |
∆2 |
= |
58 |
|
|
= −2. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∆ |
−29 |
∆ |
−29 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Таким образом, получаем следующую точку пересечения прямых: |
||||||||||||||||||||||||||
(8; −2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3) 2 − + 8 = 0, |
4 − 2 − 1 = 0. Прямые заданы общим уравне- |
|||||||||||||||||||||||||
нием. Коэффициенты при и пропорциональны: |
2 |
|
= |
−1 |
|
|
1 |
= |
1 |
, поэто- |
||||||||||||||||||
|
−2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
2 |
2 |
|
|||||||
му прямые параллельны или совпадают. Проверим условие совпадения: |
= |
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
−1 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||
≠ |
. Условие совпадения не выполняется, поэтому прямые параллель- |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
−2 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ны и не имеют общей точки.
4) − 3 + 2 = 0, 3 + − 5 = 0. Прямые заданы общим уравнением. Коэффициенты при и не пропорциональны: 13 ≠ −13 , поэтому прямые
не параллельны и, значит, пересекаются в некоторой точке. Найдём эту точку.
Объединим уравнения прямых в систему:
− 3 + 2 = 0, {3 + − 5 = 0.
Решим систему, например, методом подстановки. Выразим из второго уравнения , подставим в первое уравнение и найдём :
= −3 + 5,− 3(−3 + 5) + 2 = 0, 10 − 13 = 0,
= 1310 .
Вычислим : = −3 ∙ 1310 + 5 = 1110 .
Таким образом, получаем следующую точку пересечения прямых:
(1310 ; 1110).
5) = −4 − 12 , = −4 + 2. Прямые заданы уравнением прямой с
угловым коэффициентом. Угловые коэффициенты прямых совпадают: −4 = −4, поэтому прямые параллельны или совпадают. Проверим условие
129

совпадения: −4 = −4, − 12 ≠ 2. Условие совпадения не выполняется, поэто-
му прямые параллельны и не имеют общей точки.
6) 2 − 4 − 11 = 0, 4 − 8 − 22 = 0. Прямые заданы общим уравнением. Коэффициенты при и пропорциональны: 24 = −4−8 12 = 12 , по-
этому прямые параллельны или совпадают. Проверим условие совпадения:
24 = −−48 = −−1122
12 = 12 = 12 . Условие совпадения выполняется, поэтому прямые совпадают и
имеют бесконечно много общих точек.
7) 5 + 8 − 1 = 0, 4 − 3 + 18 = 0. Прямые заданы общим уравнением. Коэффициенты при и не пропорциональны: 54 ≠ −38 , поэтому
прямые не параллельны и, значит, пересекаются в некоторой точке. Найдём эту точку.
Объединим уравнения прямых в систему:
5 + 8 − 1 = 0, {4 − 3 + 18 = 0.
Решим систему, например, методом сложения. Умножим первое
уравнение на −4, второе уравнение умножим на 5:
−20 − 32 + 4 = 0, {20 − 15 + 90 = 0.
Сложим уравнения:
−47 + 94 = 0.
Найдём : = 2.
Подставим найденное значение , например, в первое уравнение исходной системы и найдём :
5 + 8 ∙ 2 − 1 = 0,= −3.
Таким образом, получаем следующую точку пересечения прямых:
(−3; 2).
8) 6 − 5 + 9 = 0, 4 − 3 = 0. Прямые заданы общим уравнением. Вторая прямая параллельна оси , первая прямая не параллельна этой оси, поэтому прямые не параллельны и, значит, пересекаются в некоторой точке. Найдём эту точку.
Объединим уравнения прямых в систему:
{6 − 5 + 9 = 0, 4 − 3 = 0.
Выразим из второго уравнения и подставим в первое уравнение:
= 34 , 6 ∙ 34 − 5 + 9 = 0,
29 − 5 + 9 = 0, 5 = 272 ,
= 2710 .
130
