
659
.pdf
Таким образом, получаем следующую точку пересечения прямых:
(34 ; 2710).
9) 3 + 1 = 0, − 6 + 7 = 0. Прямые заданы общим уравнением. Первая прямая параллельна оси , вторая прямая не параллельна этой оси, поэтому прямые не параллельны и, значит, пересекаются в некоторой точке. Найдём эту точку.
Объединим уравнения прямых в систему:
3 + 1 = 0, { − 6 + 7 = 0.
Выразим из первого уравнения и подставим во второе уравнение:
= − 13 ,− 6 ∙ (− 13) + 7 = 0.
Отсюда = −9.
Таким образом, получаем следующую точку пересечения прямых:
(−9; − 13 ).
10) = − 12 + 1, 7 + 14 + 6 = 0. Первая прямая задана уравнени-
ем прямой с угловым коэффициентом, вторая прямая задана общим уравнением. Преобразуем уравнение второй прямой к уравнению с угловым коэффициентом:
= − 12 − 37 . Угловые коэффициенты прямых совпадают: − 12 = − 12 , поэтому прямые параллельны или совпадают. Проверим условие совпадения: − 12 = − 12 , 1 ≠ − 37 . Условие совпадения не выполняется, поэтому прямые
параллельны и не имеют общей точки.
11) 8 + 3 = 0, 5 − 2 = 0. Прямые заданы общим уравнением. Первая прямая параллельна оси , вторая прямая не параллельна этой оси , поэтому прямые не параллельны и, значит, пересекаются в некоторой точке. Найдём эту точку.
Объединим уравнения прямых в систему:
8 + 3 = 0, {5 − 2 = 0.
Отсюда = − 38 , = 25 . Таким образом, получаем следующую точку пересечения прямых: (− 38 ; 25 ).
Ответ: 1) (4; −5); 2) (8; −2); 3) прямые не пересекаются; 4) (1310 ; 1110); 5) прямые не пересекаются; 6) прямые совпадают, то есть име-
ют бесконечно много общих точек; 7) (−3; 2); 8) (34 ; 2710); 9) (−9; − 13 ); 10) прямые не пересекаются; 11) (− 38 ; 25 ).
Пример. 3.42. Найти проекцию точки (−8; 12) на прямую, проходящую через точки (2; −3) и (−5; 1).
Решение. Проекцией точки на прямую, проходящую через точки и является основание перпендикуляра, опущенного из точки на данную
131

прямую. Основание перпендикуляра обозначим через ′. Это и будет искомая проекция точки . Сделаем схематичный чертёж (рис. 3.45).
′
Рис. 3.45. Нахождение проекции точки на прямую (к Примеру 3.42)
Точка ′ является точкой пересечения перпендикулярных прямых′ и . Составим уравнение прямой, проходящей через точки и ′.
Найдём угловой коэффициент прямой, проходящей через точки и
:
|
= 2− 1 = 1−(−3) = − |
4 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2− 1 |
|
−5−2 |
|
7 |
|||||||
|
|
|||||||||||
Далее найдём угловой коэффициент прямой, проходящей через точки |
||||||||||||
и ′, учитывая, что прямые, |
проходящие через точки и , и ′ пер- |
|||||||||||
пендикулярны: |
|
|
|
|
|
|
|
|||||
′ = − |
1 |
= − |
1 |
= |
7 |
. |
|
|
||||
|
4 |
4 |
|
|
||||||||
|
|
|
|
|
−7 |
|
|
|||||
Для составления уравнения прямой, проходящей через точки и ′,
воспользуемся уравнением прямой, проходящей через данную точку с данным угловым коэффициентом: − 0 = ( − 0). Запишем это уравнение
в обозначениях нашего примера: − = ′( − ), где = −8, =
12, ′ = 74 .
Подставим и преобразуем:
− 12 = 74 ( − (−8)), 4( − 12) = 7( + 8),
7 − 4 + 104 = 0.
Таким образом, получили уравнение прямой, проходящей через точки и ′:
7 − 4 + 104 = 0.
Далее составим уравнение прямой, проходящие через точки и . Воспользуемся уравнением прямой, проходящей через данную точку с данным угловым коэффициентом: − 0 = ( − 0). В качестве данной точки возьмём, например, точку , угловой коэффициент найден выше. Запишем это уравнение в обозначениях нашего примера: − = ( − ), где
= 2, = −3, = − 47 . Подставляем:
− (−3) = − 47 ( − 2), 7( + 3) = −4( − 2),
4 + 7 + 13 = 0.
132
Таким образом, получили уравнение прямой, проходящей через точки и :
4 + 7 + 13 = 0.
Найдём искомую точку ′, решив совместно уравнения прямых, про-
ходящих через точки и , и ′:
7 − 4 + 104 = 0, { 4 + 7 + 13 = 0.
Умножим первое уравнение на 4, второе уравнение умножим на −7:
28 − 16 + 416 = 0, {−28 − 49 − 91 = 0.
Сложим уравнения:
−65 + 325 = 0,= 5.
Подставим найденное значение, например, в первое уравнение:
7 − 4 ∙ 5 + 104 = 0,= −12.
Искомая точка: ′(−12; 5).
Ответ: ′(−12;5).
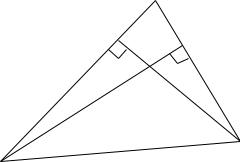
Пример. 3.43. Составить уравнения сторон треугольника, если даны одна из его вершин (−4; −5) и уравнения двух высот 5 + 3 − 4 = 0 и 3 + 8 + +13 = 0.
Решение. Выясним, лежит ли точка на данных высотах. Для этого подставим координаты точки в уравнение каждой высоты. Подставляем в уравнение первой высоты: 5 ∙ (−4) + 3 ∙ (−5) − 4 = 0. Отсюда: −39 ≠ 0, поэтому точка не лежит на первой высоте. Подставляем в уравнение второй высоты: 3 ∙ (−4) + 8 ∙ (−5) + 13 = 0. Отсюда: −39 ≠ 0, поэтому точкане лежит на второй высоте. Таким образом, заданные высоты проведены из вершин треугольника, отличных от точки .
Остальные вершины треугольника обозначим через и , основания высот обозначим через и . Выполним схематичный чертёж (рис. 3.46).
Рис. 3.46. Составление уравнений сторон треугольника по заданной вершине и двум высотам (к Примеру 3.43)
Высоты заданы общим уравнением прямой. Преобразуем их к уравнению прямой с угловым коэффициентом: = + . Уравнение высоты
133

: = − |
5 |
+ |
4 |
, уравнение высоты : = − |
3 |
− |
13 |
. Выпишем угловые |
||||||||||||||
|
|
8 |
|
|||||||||||||||||||
3 |
3 |
|
5 |
|
|
|
|
|
3 |
|
|
|
|
8 |
|
|||||||
коэффициенты высот: |
= − |
, |
|
|
= − |
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3 |
|
8 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Найдём угловой коэффициент стороны , используя условие пер- |
||||||||||||||||||||||
пендикулярности прямых: = − |
1 |
|
= − |
1 |
|
= |
|
3 |
. Аналогично, найдём уг- |
|||||||||||||
|
|
5 |
5 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
||
ловой коэффициент стороны , используя условие перпендикулярности
прямых: |
= − |
1 |
= − |
1 |
|
= |
8 |
. |
|
|
|
||||||
|
|
3 |
3 |
|||||
|
|
|
|
−8 |
|
|
|
|
Составим уравнения сторон треугольника, используя уравнение пря-
мой с данным угловым коэффициентом и проходящей через данную точку:
− 0 = ( − 0).
Составим уравнение стороны, проходящей через точки и . Для этой прямой известен угловой коэффициент = 83 и точка (−4; −5).
Подставляем:
− (−5) = 83 ( − (−4)).
Преобразуем до общего уравнения прямой:
3( + 5) = 8( + 4), 8 − 3 + 17 = 0.
Таким образом, общее уравнение стороны, проходящей через точки
и : 8 − 3 + 17 = 0.
Аналогично составляем уравнение стороны, проходящей через точки
и . Для этой прямой известен угловой коэффициент = 35 и точка
(−4; −5). Подставляем:
− (−5) = 35 ( − (−4)).
Преобразуем до общего уравнения прямой:
5( + 5) = 3( + 4), 3 − 5 − 13 = 0.
Таким образом, общее уравнение стороны, проходящей через точки
и : 3 − 5 − 13 = 0.
Далее найдём координаты точки , как точки пересечения стороныи высоты . Объединим их уравнения в систему и решим её методом
сложения:
8 − 3 + 17 = 0, { 5 + 3 − 4 = 0.
Сложим уравнения:
13 + 13 = 0, = −1, = 3. Таким образом, (−1; 3).
Далее найдём координаты точки , как точки пересечения стороныи высоты . Объединим их уравнения в систему и решим её методом
сложения:
3 − 5 − 13 = 0, {3 + 8 + 13 = 0.
Вычтем из второго уравнения первое:
13 + 26 = 0, = −2, = 1. Таким образом, (1; −2).
134
Составим уравнение стороны, проходящей через точки и С. Найдём
угловой коэффициент: = |
−2−3 |
|
= − |
5 |
|
. Далее воспользуемся уравнени- |
|
|
|||||
|
1−(−1) |
2 |
|
|||
|
|
|||||
ем прямой с данным угловым коэффициентом и проходящей через данную
точку: − 0 = = ( − 0). Угловой коэффициент известен. В качестве данной точки
возьмём точку (−1; 3). Подставляем:
− 3 = − 52 ( − (−1)),
Преобразуем до общего уравнения прямой:
2( − 3) = −5( + 1), 5 + 2 − 1 = 0.
Таким образом, общее уравнение стороны, проходящей через точки
и С: 5 + 2 − 1 = 0.
Ответ: 8 − 3 + 17 = 0, 3 − 5 − 13 = 0, 5 + 2 − 1 = 0.
3.11. Расстояние от точки до прямой
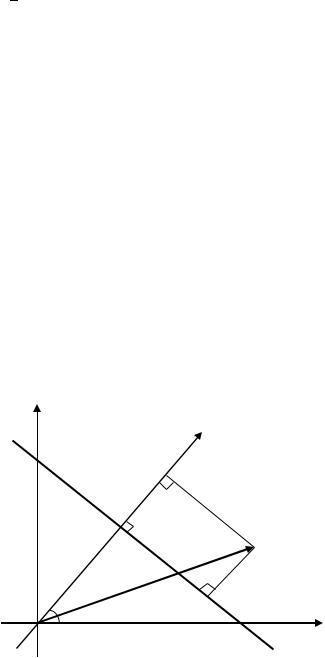
Рассмотрим произвольную прямую . Проведём через начало координат прямую перпендикулярно прямой . Прямую называют нормалью. На нормали зададим направление.
Обозначим:
0( 0; 0) – произвольная точка плоскости;– расстояние от точки 0 до прямой;
– расстояние от начала координат до прямой;– угол, который образует нормаль c осью ;– проекция точки 0 на нормаль;
– точка пересечения прямой с нормалью (рис. 3.47).
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Рис. 3.47. Расстояние от точки до прямой
Отклонением точки 0 от прямой называют число , если точка лежит с той стороны от прямой, куда направлена нормаль и называют число − , если точка лежит с другой стороны от прямой. Отклонение обозначают и = ± . Следовательно, = | |.
135

По чертежу можно записать (на чертеже = ):
= = | | − | | = пр ̅̅̅̅̅̅0 − .
При выводе нормального уравнения прямой была получена следующая формула для проекции: пр ̅̅̅̅̅ = cos + sin , где и – коорди-
наты произвольной точки прямой. Применяя эту формулу к точке 0, по-
лучаем:
пр ̅̅̅̅̅̅0 = 0 cos + 0 sin .
Тогда:
= пр ̅̅̅̅̅̅0 − = 0 cos + 0 sin − .
Таким образом, отклонение точки от прямой вычисляется по фор-
муле:
= 0 cos + 0 sin − .
Правая часть этой формулы совпадает с левой частью нормального уравнения прямой: cos + sin − = 0, в которую вместо текущих координат подставлены координаты точки 0. Поэтому для вычисления отклонения точки от прямой надо в левую часть нормального уравнения подставить координаты данной точки.
Часто прямая задаётся общим уравнением: + + = 0. Поэтому для вычисления отклонения точки от прямой надо уравнение прямой привести к нормальному. Получим формулу, которая позволяет, зная общее уравнение прямой, вычислить отклонение, не переходя к нормальному уравнению.
В п. 3.7. был указан способ перехода от общего уравнению к нормальному путём умножения общего уравнения на нормирующий множи-
тель = ± |
|
1 |
, где знак |
выбирается противоположным знаку слагае- |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
√2+ 2 |
|||||||||||||||||||||||||||||
мого . Умножив общее уравнение на , получаем: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
+ + = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Сравнивая это уравнение с нормальным, можно записать: |
|
|
|
|
|
||||||||||||||||||||||||
cos = = ± |
|
|
|
|
, sin = = ± |
|
|
|
|
, − = = ± |
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
+ |
2 |
2 |
|
2 |
2 |
+ |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
√ + |
|
|
|
|
√ |
|
|
||||||||
Подставим эти выражения в формулу отклонения: |
|
|
|
|
|
||||||||||||||||||||||||
= ± |
|
|
|
|
± |
|
|
|
± |
|
|
= ± |
0+ 0+ |
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
√2+ 2 0 |
|
|
√2+ 2 0 |
√2+ 2 |
|
|
|
√2+ 2 |
|
|
|
|
|
|||||||||||||
Таким образом, отклонение можно вычислять по формуле:
= ± 0+ 0+ . √2+ 2
Отсюда получаем следующую формулу для вычисления расстояния от точки до прямой:
= | 0+ 0+ | . √2+ 2
Выражение под знаком модуля представляет собой левую часть общего уравнения прямой, в которую подставлены координаты точки 0. В знаменателе и – коэффициенты при и в общем уравнении прямой.
Пример. 3.44. Найти расстояние от точки до прямой:
1)(2; −1), 4 + 3 + 10 = 0;
2)(−2; 3), 3 − 4 − 2 = 0;
3)(−2; −3), 2 − 3 + 6 = 0;
136
4) (1; −2), − 2 − 5 = 0.
Решение. Применяем формулу нахождения расстояния от точки до
прямой: = | 0+ 0+ | . В левую часть данного уравнения прямой под-
√ 2+ 2
ставляем координаты точки и записываем полученное число под знак модуля. В знаменателе и – коэффициенты при и в данном уравнении прямой.
1) |
= |
|4∙2+3∙(−1)+10| |
= |
|
|15| |
|
= |
15 |
|
= 3. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
√42+32 |
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
||||||||||||||||||||
2) |
= |
|3∙(−2)−4∙3−2| |
= |
|
|
|−20| |
= |
20 |
= 4. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
2 |
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
||||||||||||||||||||
|
|
√3 |
+(−4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|2∙(−2)−3∙(−3)+6| |
|
|
|
|11| |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3) |
= |
= |
|
= |
|
|
11 |
= |
11√13 |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
√22+(−3)2 |
|
|
|
|
|
|
|
|
|
|
|
|
√13 |
|
|
|
√13 |
13 |
|
||||||||||||||
4) |
= |
|1−2∙(−2)−5| |
= |
|0| |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
2 |
|
|
√5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
√1 +(−2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: 1) 3; 2) 4; 3) 11√13 ; 4) 0.
13
Пример. 3.45. Вычислить расстояние между параллельными прямы-
ми:
1)4 − 3 + 15 = 0 и 8 − 6 + 25 = 0;
2)5 − 2 − 1 = 0 и 5 − 2 + 7 = 0.
Решение. Расстояние между параллельными прямыми вычислим как расстояние от некоторой точки одной прямой до другой прямой.
1)Найдём точку, например, первой прямой. Зададим = 0. Тогда
= 5. Находим расстояние от точки (0; 5) до прямой 8 − 6 + 25 = 0:
= |8∙0−6∙5+25| = |−5| = 5 = 1 √82+(−6)2 10 10 2 .
2)Найдём точку, например, первой прямой. Зададим = 0. Тогда
= − 12 . Находим расстояние от точки (0; − 12) до прямой 5 − 2 + 7 = 0:
|
|5∙0−2∙(−1)+7| |
|
|
| | |
|
|
|
|
|
||||||||
|
|
|
|
8√29 |
|||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
|
|
= |
|
|
|
= |
|
. |
|||
|
|
|
|
|
|
|
|
|
|
29 |
|||||||
√ |
52+22 |
|
|
|
√29 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: 1) |
1 |
; 2) |
8√29 |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|||
Пример. 3.46. Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми 3 + 4 − 1 = 0 и 5 + 12 − 2 = 0.
Решение. Известен факт, что все точки, расположенные на биссектрисе угла, равноудалены от сторон угла, то есть расстояния от любой точ-
ки биссектрисы до сторон угла равны. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
Данные прямые обозначим 1 |
и 2, биссектрисы обозначим 1 и 2. |
|||||||||||||||
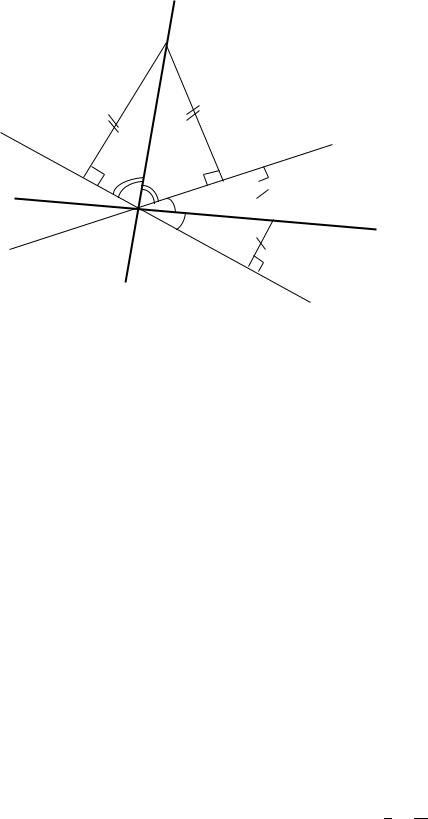
Пусть ( ; ) – произвольная точка биссектрисы. Выполним схематичный |
||||||||||||||||||||||
чертёж (рис. 3.48). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Запишем выражение расстояния от точки до прямой 3 + 4 − |
||||||||||||||||
−1 = 0, |
воспользовавшись формулой расстояния от точки до прямой = |
|||||||||||||||||||||
| 0+ 0+ | |
. Получаем: = |
|3 +4 −1| |
= |
|3 +4 −1| |
. Аналогично запишем вы- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
+ |
2 |
|
√3 |
2 |
+4 |
2 |
5 |
|||||||||||||
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ражение расстояния от этой точки до прямой 5 + 12 − 2 = 0: = |
||||||||||||||||||||||
= |
|5 +12 −2| |
= |
|5 +12 −2| |
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
√5 |
2 |
|
2 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
137 |
|
|
|||
2
( ; )
1
 1 ( ; )
1 ( ; )
2
Рис. 3.48. Составление уравнений биссектрис углов, образованных двумя пересекающимися прямыми (к Примеру 2.46)
Приравниваем полученные выражения:
|3 +4 −1| |
= |
|5 +12 −2| |
. |
|
5 |
|
13 |
||
|
|
|
||
Раскрывая знак модуля, получаем два уравнения:
3 +4 −1 |
= |
5 +12 −2 |
и |
3 +4 −1 |
= − |
5 +12 −2 |
. |
||
|
|
|
|
|
|
||||
5 |
|
13 |
|
5 |
|
13 |
|
||
Преобразуем первое уравнение:
13(3 + 4 − 1) = 5(5 + 12 − 2), 39 + 52 − 13 = 25 + 60 − 10, 14 − 8 − 3 = 0.
Таким образом, уравнение одной биссектрисы 14 − 8 − 3 = 0.
Преобразуем второе уравнение:
13(3 + 4 − 1) = −5(5 + 12 − 2), 39 + 52 − 13 = −25 − 60 + 10, 64 + 112 − 23 = 0.
Таким образом, уравнение другой биссектрисы 64 + 112 − 23 =
= 0.
Ответ: 14 − 8 − 3 = 0, 64 + 112 − 23 = 0.
Пример. 3.47. Даны уравнения двух сторон квадрата 5 + 12 − −10 = 0, 5 + 12 + 29 = 0. Составить уравнения двух других его сторон при условии, что точка (−3; 5) лежит на стороне этого квадрата.
Решение. Заметим, что даны уравнения двух параллельных сторон квадрата, так как для заданных прямых выполняется условие параллельно-
сти, а именно, коэффициенты при неизвестных пропорциональны: 55 = 1212 .
Выясним, лежит ли точка на данных прямых. Для этого подставим координаты точки в каждое уравнение. Подставляем в первое уравнение: 5 ∙ (−3) + 12 ∙ 5 − 10 = 0. Отсюда 35 ≠ 0, поэтому точка не лежит на первой прямой. Подставляем во второе уравнение: 5 ∙ (−3) + 12 ∙ 5 + 29 =
138

= 0. Отсюда 74 ≠ 0, поэтому точка не лежит на второй прямой. Таким образом, точка не лежит на данных прямых и, значит, она лежит на прямых, содержащих другие стороны квадрата. Эти прямые перпендикулярны данным прямым.
Обозначим квадрат . Пусть стороны, лежащие на заданных прямых, будут и . Пусть точка лежит на стороне . Требуется найти уравнения сторон и . Можно заметить, что существует ещё один квадрат, две противоположные стороны которого лежат на заданных прямых. Сторона, лежащая на прямой, перпендикулярной данным прямым, совпадает со стороной . Вторую сторону, перпендикулярную данным прямым, обозначим 1 1. Второй квадрат: 1 1. Выполним схематичный чертёж (рис. 3.49).
1 |
|
|
5 + 12 + 29 = 0

|
|
|
5 + 12 − 10 = 0 |
|
|
|
|
|
|
1 |
|
|
||
Рис. 3.49. Составление уравнений сторон квадрата (к Примеру 3.47)
Найдём угловой коэффициент прямой, проходящей через точки и. Для этого преобразуем общее уравнение этой прямой к уравнению прямой с угловым коэффициентом = + , где – угловой коэффициент прямой.
Преобразуем уравнение прямой, проходящей через точки и :
12 = −5 − 29,
= − 125 − 1229 .
Запишем угловой коэффициент прямой: = − 125 .
Учитывая, что прямые, проходящие через точки и , и , перпендикулярны, найдём угловой коэффициент прямой, проходящей через
точки и : = − 1 = − 15 = 12 .
−12 5
Составим уравнение прямой, проходящей через точки и , используя уравнение прямой с данным угловым коэффициентом и проходящей
через данную точку: − 0 = ( − 0). Здесь ( 0; 0) – данная точка прямой, – угловой коэффициент прямой. В нашем примере данная точка –
это точка (−3; 5) и
= = 125 .
Подставляем:
− 5 = 125 ( − (−3)).
139

Преобразуем к общему уравнению прямой:
5( − 5) = 12( + 3), 12 − 5 + 61 = 0.
Таким образом, уравнение стороны квадрата, лежащей на прямой, проходящей через точки и , то есть общей стороны двух квадратов:
12 − 5 + 61 = 0.
Далее составим уравнения сторон и 1 1.
Найдём расстояние между точками и , которое равно расстоянию между заданными параллельными прямыми. Найдём одну точку прямой, проходящей через точки и . Для этого возьмём = 0. Подставим в уравнение прямой: 5 + +12 ∙ 0 − 10 = 0. Отсюда = 2. Точка прямой: (2; 0).
Расстояние между параллельными прямыми найдём как расстояние от точки (2; 0) до прямой, заданной уравнением 5 + 12 + 29 = 0. Воспользуемся формулой нахождения расстояния от точки до прямой: =
= |
| 0+ 0+ | |
. Подставляем: | | = |
|5∙2+12∙0+29| |
= |
39 |
= 3. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
+ |
2 |
|
2 |
2 |
13 |
||||||||
|
|
√ |
|
|
|
√5 |
+12 |
|
|
|
||||
|
|
|
Учитывая, что | | = | | = | 1 1| = 3, применим формулу рассто- |
|||||||||||
яния от точки до прямой для прямой, проходящей через точки и : 12 − 5 + 61 = 0 и произвольной точки ( ; ) сторон и 1 1:
|12 −5 +61| = 3
√122+52 .
Раскрывая знак модуля, получаем два уравнения:
12 −5 +61 |
= 3 и |
12 −5 +61 |
= −3. |
||
13 |
|
13 |
|
||
|
|
|
|
||
Преобразуем первое уравнение:
12 − 5 + 61 = 39, 12 − 5 + 22 = 0.
Преобразуем второе уравнение:
12 − 5 + 61 = −39, 12 − 5 + 100 = 0.
Ответ: 12 − 5 + 61 = 0, 12 − 5 + 22 = 0 или 12 − 5 + 61 = = 0, 12 − 5 + 100 = 0.
3.12. Уравнение пучка прямых
Пусть прямые 1 и 2 заданы общим уравнением:
1 + 1 + 1 = 0 и 2 + 2 + 2 = 0.
Пусть эти прямые пересекаются в точке . Множество всех прямых, проходящих через эту точку, называется пучком прямых с центром в точке
(рис. 3.50).
Если и – действительные числа, то уравнение пучка прямых с
центром в точке имеет вид:
( 1 + 1 + 1) + ( 2 + 2 + 2) = 0.
Разделив уравнение пучка прямых на число ≠ 0, и, обозначив через , получаем уравнение пучка прямых в следующем виде:
140
