659

Рис. 3.50.Пучок прямых с центром в точке

1 + 1 + 1 + ( 2 + 2 + 2) = 0.

Пример. 3.48. Найти центр пучка прямых, данного уравнением 2 + 3 − 1 + ( − 2 − 4) = 0.

Решение. Для нахождения центра пучка прямых решим совместно

уравнения основных прямых пучка. Составляем систему уравнений:

2 + 3 − 1 = 0, { − 2 − 4 = 0.

Решим систему методом сложения. Умножив второе уравнение на

−2, получаем:

2 + 3 − 1 = 0, {−2 + 4 + 8 = 0.

Сложив уравнения, получаем:

7 + 7 = 0, = −1.

Подставим = −1 во второе уравнение исходной системы:

− 2 ∙ (−1) − 4 = 0, = 2.

Таким образом, центр пучка: точка (2; −1).

Ответ: (2; −1).

Пример. 3.49. Найти уравнение прямой, принадлежащей пучку прямых + 2 − 5 + (3 − 2 + 1) = 0 и: 1) проходящей через точку(3; −1); 2) параллельно прямой 4 + 3 + 5 = 0; 3) перпендикулярно прямой 2 + 3 + 7 = 0.

Решение.

1) Подберём значение параметра так, чтобы прямая прошла через

точку (3; −1). Подставим координаты этой точки в уравнение пучка:

3 + 2 ∙ (−1) − 5 + (3 ∙ 3 − 2 ∙ (−1) + 1) = 0,

−4 + 12 = 0,= 13 .

Таким образом, при = 13 из всех прямых пучка получим искомую

прямую. Подставим = 13 в уравнение пучка:

+ 2 − 5 + 13 (3 − 2 + 1) = 0.

Преобразуем к общему уравнению прямой:

141

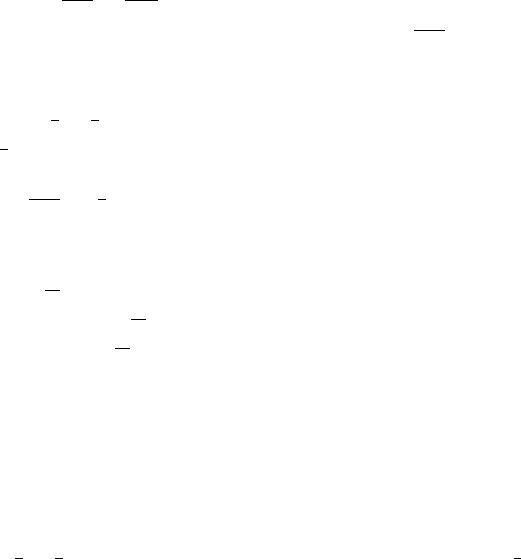
3( + 2 − 5) + 3 − 2 + 1 = 0, 6 + 4 − 14 = 0, 3 + 2 − 7 = 0.

Таким образом, уравнение искомой прямой: 3 + 2 − 7 = 0.

2) Преобразуем уравнение пучка прямых сначала к общему уравнению прямой + + = 0:

(1 + 3 ) + (2 − 2 ) + (−5 + ) = 0.

Затем преобразуем полученное уравнение к уравнению прямой с уг-

ловым коэффициентом: = + , где – угловой коэффициент прямой:

(2 − 2 ) = −(1 + 3 ) − (−5 + ),

= − 1+3 − −5+ . 2−2 2−2

Запишем угловой коэффициент прямых пучка: = − 1+32−2 .

В этом пункте требуется из всех прямых пучка выбрать ту, которая параллельна прямой 4 + 3 + 5 = 0. Найдём угловой коэффициент этой прямой, приведя её уравнение к уравнению прямой с угловым коэффициен-

том: = − 43 − 53 . Запишем угловой коэффициент данной прямой: 1 = = − 43 . Учитывая, что параллельные прямые имеют равные угловые коэф-

фициенты, получаем следующее уравнение для нахождения параметра :

− 1+32−2 = − 43 .

Найдём :

3(1 + 3 ) = 4(2 − 2 ), 17 = 5,

= 175 .

Подставим = 175 в уравнение пучка:

+ 2 − 5 + 175 (3 − 2 + 1) = 0.

Преобразуем к общему уравнению прямой:

17( + 2 − 5) + 5(3 − 2 + 1) = 0, 32 + 24 − 80 = 0, 4 + 3 − 10 = 0.

Таким образом, уравнение искомой прямой: 4 + 3 − 10 = 0.

3) В этом пункте требуется из всех прямых пучка выбрать ту, которая перпендикулярна прямой 2 + 3 + 7 = 0. Найдём угловой коэффициент этой прямой, приведя её уравнение к уравнению прямой с угловым коэффициентом:

= − 23 − 73 . Запишем угловой коэффициент данной прямой: 1 = − 23 .

Учитывая, что произведение угловых коэффициентов перпендикулярных прямых равно −1, найдём угловой коэффициент прямой, перпендикулярной данной прямой:

падает с угловым коэффициентом второго уравнения пучка. Искомой пря-

142

мой является вторая прямая пучка, поскольку она перпендикулярна заданной прямой и проходит через центр пучка.

Таким образом, уравнение искомой прямой: 3 − 2 + 1 = 0.

Ответ: 1) 3 + 2 − 7 = 0; 2) 4 + 3 − 10 = 0; 3) 3 − 2 + 1 = 0.

Пример. 3.50. Даны уравнения сторон треугольника + 2 − 1 = 0, 5 + 4 − 17 = 0, − 4 + 11 = 0. Не определяя координат его вершин, составить уравнения высот этого треугольника.

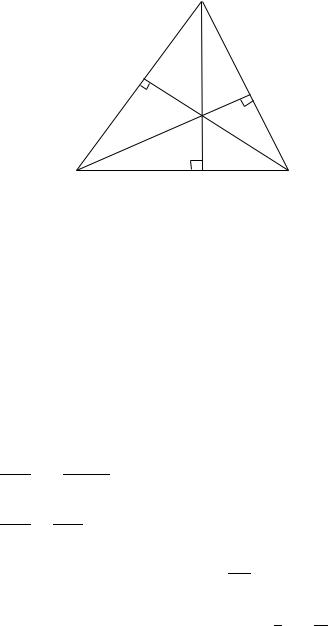
Решение. Вершины треугольника обозначим точками , , . Пусть сторона задана уравнением + 2 − 1 = 0, сторона задана уравнением 5 + 4 − 17 = 0, сторона задана уравнением − 4 + 11 = 0. Основание высоты треугольника, проведённой из вершины , обозначим1, из вершины обозначим 1, из вершины обозначим 1. Выполним схематичный чертёж (рис. 3.51).

Рис. 3.51. Составление уравнений высот треугольника по известным уравнениям его сторон (к Примеру 3.50)

Перейдём к составлению уравнений высот.

Высоту 1 будем рассматривать как прямую пучка, образованного

сторонами и треугольника. Составим уравнение этого пучка:

+ 2 − 1 + ( − 4 + 11) = 0.

Преобразуем уравнение пучка прямых сначала к общему уравнению прямой + + = 0:

(1 + ) + (2 − 4 ) + (−1 + 11 ) = 0.

Затем преобразуем полученное уравнение к уравнению прямой с уг-

ловым коэффициентом: = + , где – угловой коэффициент прямой:

(2 − 4 ) = −(1 + ) − (−1 + 11 ),

= − 1+ − −1+11 .

2−4 2−4

Запишем угловой коэффициент прямых пучка:

= − 2−41+ = 41+−2 .

Высота 1 перпендикулярна стороне , поэтому их угловые ко-

эффициенты связаны равенством 1 = − 1 . Найдём угловой коэффици-

ент стороны . Для этого приведём общее уравнение стороны к уравнению прямой с угловым коэффициентом: = − 54 + 174 .Тогда угловой ко-

143

Из всех прямых пучка выберем ту, угловой коэффициент которой равен 45 . Получаем уравнение для нахождения параметра :

1+ = 4 .

4 −2 5

Найдём :

5(1 + ) = 4(4 − 2), 11 = 13,

= 1311 .

Подставим = 1311 в уравнение пучка, записанного в общем виде:

(1 + 1311) + (2 − 4 ∙ 1311) + (−1 + 11 ∙ 1311) = 0.

Преобразуем:

2411 − 3011 + 12 = 0,

114 − 115 + 2 = 0, 4 − 5 + 22 = 0.

Таким образом, уравнение высоты 1: 4 − 5 + 22 = 0. Аналогично составим уравнения остальных высот. Составим уравнение высоты 1.

Высоту 1 будем рассматривать как прямую пучка, образованного

сторонами и треугольника. Составим уравнение этого пучка:

+ 2 − 1 + (5 + 4 − 17) = 0.

Преобразуем уравнение пучка прямых сначала к общему уравнению прямой + + = 0:

(1 + 5 ) + (2 + 4 ) + (−1 − 17 ) = 0.

Затем преобразуем полученное уравнение к уравнению прямой с уг-

ловым коэффициентом: = + , где – угловой коэффициент прямой:

(2 + 4 ) = −(1 + 5 ) − (−1 − 17 ),

= − 1+5 − −1−17 .

2+4 2+4

Запишем угловой коэффициент прямых пучка:

= − 1+52+4 .

Высота 1 перпендикулярна стороне , поэтому их угловые ко-

эффициенты связаны равенством 1 = − 1 . Найдём угловой коэффици-

ент стороны . Для этого приведём общее уравнение стороны к урав-

Из всех прямых пучка выберем ту, угловой коэффициент которой равен −4 . Получаем уравнение для нахождения параметра :

144

− 1+52+4 = −4 .

Найдём :

1 + 5 = 4(2 + 4 ),

11 = −7,= − 117 .

Подставим = − 117 в уравнение пучка, записанного в общем виде:

(1 + 5 ∙ (− 117 )) + (2 + 4 ∙ (− 117 )) + (−1 − 17 ∙ (− 117 )) = 0.

Преобразуем:

− 2411 − 116 + 10811 = 0,

24 + 6 − 108 = 0. 4 + − 18 = 0.

Таким образом, уравнение высоты 1: 4 + − 18 = 0. Составим уравнение высоты 1.

Высоту 1 будем рассматривать как прямую пучка, образованного

сторонами и треугольника. Составим уравнение этого пучка:

− 4 + 11 + (5 + 4 − 17) = 0.

Преобразуем уравнение пучка прямых сначала к общему уравнению прямой + + = 0:

(1 + 5 ) + (−4 + 4 ) + (11 − 17 ) = 0.

Затем преобразуем полученное уравнение к уравнению прямой с уг-

ловым коэффициентом: = + , где – угловой коэффициент прямой:

(−4 + 4 ) = −(1 + 5 ) − (11 − 17 ),

Из всех прямых пучка выберем ту, угловой коэффициент которой ра-

вен 2 . Получаем уравнение для нахождения параметра :

1+54−4 = 2 .

Найдём :

1 + 5 = 2(4 − 4 ),

13 = 7,

= 137 .

Подставим = 137 в уравнение пучка, записанного в общем виде:

145

(1 + 5 ∙ 137 ) + (−4 + 4 ∙ 137 ) + (11 − 17 ∙ 137 ) = 0.

Преобразуем:

4813 − 2413 + 2413 = 0,

48 − 24 + 24 = 0, 2 − + 1 = 0.

Таким образом, уравнение высоты 1: 2 − + 1 = 0.

Ответ: 4 − 5 + 22 = 0, 4 + − 18 = 0, 2 − + 1 = 0.

3.13. Полярное уравнение прямой

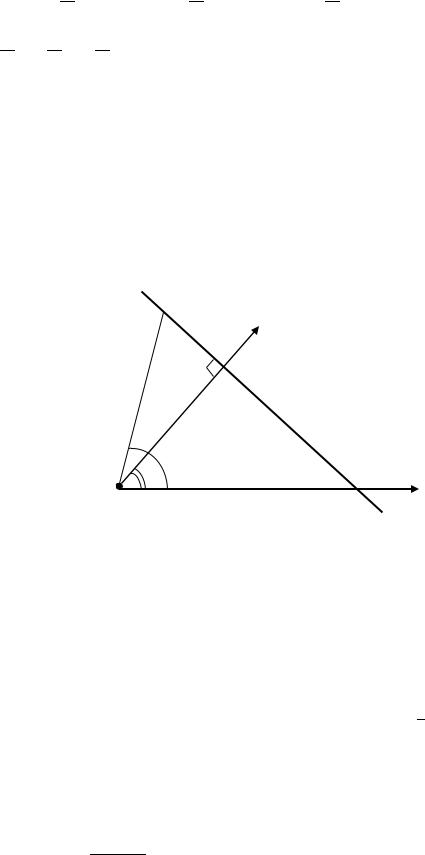
Рассмотрим прямую в полярной системе координат. Пусть задано расстояние от полюса до прямой и полярный угол нормали . Пусть( ; ) – произвольная точка прямой, где и – полярные координаты точки. Обозначим через точку пересечения нормали с прямой (рис. 3.52).

Рис. 3.52. Прямая в полярной системе координат

Полученное уравнение называется полярным уравнением прямой.

Пример. 3.51. Записать полярное уравнение прямой, если расстояние от полюса до прямой равно 4 и полярный угол нормали равен 4 .

Решение. Полярное уравнение прямой, если известно расстояние от

– расстояние от полюса до прямой, – полярный угол нормали. Подставля-

Ответ: = 4 .

cos( −4)

146

Пример. 3.52. Вывести полярное уравнение прямой, если известен угол наклона прямой к полярной оси и отрезок , который отсекает прямая на полярной оси, считая от полюса.

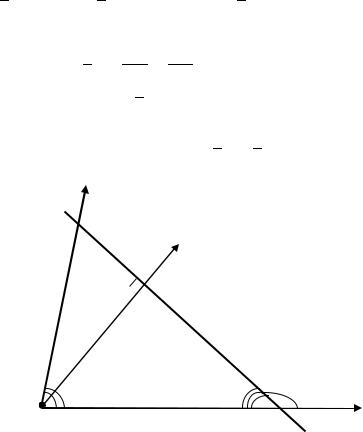
Решение. Пусть (; ) – произвольная точка прямой, где и – полярные координаты точки. Обозначим через точку пересечения нормали с прямой, через обозначим точку пересечения прямой с полярной осью. Выполним схематичный чертёж (рис. 3.53).

Из треугольника :

= 2 − = 2 − ( − ) = − 2 .

Запишем косинус этого угла:

| | = | | . | |

Отсюда: | | = cos ( − 2) = sin .

Из треугольника :

= − = − ( − 2) = 2 + − .

Рис. 3.53. Вывод полярного уравнения прямой по известному углу наклона прямой к полярной оси и отрезку, отсекаемому на полярной оси, считая от полюса

(к Примеру 3.52)

Запишем косинус этого угла:

Контрольные вопросы

1.Что называется углом наклона прямой?

147

2.Что называется угловым коэффициентом прямой? Запишите формулу его нахождения через координаты двух точек прямой.

3.Запишите уравнение прямой с угловым коэффициентом.

4.Запишите уравнение прямой с данным угловым коэффициентом и проходящей через данную точку.

5.Запишите уравнение прямой, проходящей через две данные

точки.

6.Запишите общее уравнение прямой.

7.Запишите уравнение прямой в отрезках, сформулируйте его геометрический смысл.

8.Запишите нормальное уравнение прямой. Как можно перейти от общего уравнения прямой к нормальному?

9.Что называется пучком прямых. Запишите уравнение пучка

прямых.

10.Запишите формулу нахождения угла между двумя прямыми.

11.Сформулируйте условия параллельности, перпендикулярности

исовпадения прямых, когда прямые заданы уравнением с угловым коэффициентом.

12.Сформулируйте условия параллельности, перпендикулярности

исовпадения прямых, когда прямые заданы общим уравнением.

13.Как найти точку пересечения двух прямых на плоскости?

14.Что называется отклонением точки от прямой? Запишите формулу его вычисления.

15.Запишите формулу нахождения расстояния от точки до пря-

мой.

16.Запишите полярное уравнение прямой.

Упражнения

Угловой коэффициент прямой

1.Найти угловой коэффициент прямой, проходящей через точки:

Уравнение прямой с угловым коэффициентом

2.Среди приведённых уравнений указать уравнения прямой с уг-

148

3.Прямая задана уравнением = 5 − 8. Найти угловой коэффициент прямой и величину отрезка, отсекаемого прямой на оси ординат.

4.Дана прямая = −3 + 5. Проверить, проходит ли она через

следующие точки (−1; 8), (3; −4), (− 12 ; 132 ), (− 12 ; 4), (2; 0),

(53 ; 0), (0; 0).

5.Точки , , , , , лежат на прямой = 2 + 4. Абсциссы

этих точек соответственно равны 3, −5, 0, 12 , − 13 , −2. Найти ординаты этих

точек.

6. Точки , , , , , лежат на прямой = − + 2. Ординаты этих точек соответственно равны −4, 3, 0, 14 , − 15 , 2. Найти абсциссы этих

точек.

7. Составить уравнение прямой, зная, что её угловой коэффициент равен − 117 и величина отрезка, отсекаемого прямой на оси ординат, равна 2.

8.Построить прямые, заданные следующими уравнениями:

9.Сила приложена к началу координат, и составляющие её по осям соответственно равны 5 и −2. Найти уравнение прямой, по которой направлена сила.

10.Какая линия служит графиком равномерного движения, определяемого уравнением = 0 + ?

11.Найти скорость равномерного движения, зная, что его график

пересекает ось абсцисс в точке (− 12 ; 0) и ось ординат в точке (0; 8).

Масштаб выбран так, что на оси единица длины соответствует одному часу, а на оси – одному километру. Указание. Воспользоваться уравнением прямой в отрезках и уравнением в задаче 10.

12.Точка, вышедшая из начала координат, должна одновременно

перемещаться по направлению оси абсцисс с постоянной скоростью 1 и по направлению оси ординат с постоянной скоростью 2. Найти истинную траекторию движущейся точки. Указание. В любой момент движущаяся

точка будет иметь абсциссу = 1 и ординату = 2 . Исключая из этих уравнений, получим искомую траекторию.

13.Луч света направлен по прямой = 23 − 4. Дойдя до оси абс-

цисс, луч от неё отразился. Определить точку встречи луча с осью и уравнение отражённого луча.

Уравнение прямой с данным угловым коэффициентом и проходящей через данную точку

14. Составить уравнение прямой, проходящей через точку(5; −8) и имеющей угловой коэффициент равный −2.

149

15. Составить уравнение прямой, проходящей через точку(−3; 2) и составляющей с осью абсцисс угол = 300.

Уравнение прямой, проходящей через две данные точки

16.Составить уравнение прямой, проходящей через две точки

1(5; −2) и 2(−1; 3).

17.Даны вершины треугольника (3; 2), (5; −2), (1; 0). Со-

ставить уравнения сторон треугольника.

18.Даны вершины треугольника (3; 2), (5; −2), (1; 0). Составить уравнения медиан треугольника.

19.Через точки 1(−1; 2) и 2(2; 3) проведена прямая. Определить точки пересечения этой прямой с осями координат.

20.Даны вершины треугольника (1; 1), (10; 13), (13; 6). Со-

ставить уравнение биссектрисы, проведённой из точки .

Общее уравнение прямой

21.Среди приведённых уравнений указать общие уравнения пря-

мой:

22.Преобразовать уравнение прямой с угловым коэффициентом

= −4 + 3 к общему уравнению.

23.Прямая задана общим уравнением 3 + 7 − 9 = 0. Найти её угловой коэффициент.

24.Дана прямая − 2 + 1 = 0. Проверить, проходит ли она через точки (−2; 1), (−1; 0), (−1; 13), (1; −2), (32 ; 54), (0; 12), (0; 0).

25.Точки , , , , лежат на прямой 2 − 5 + 3 = 0. Абсцис-

сы этих точек соответственно равны 0; −1; 1; 12 ; − 15 . Найти ординаты этих

точек.

26. Точки , , , , лежат на прямой 4 − 3 + 2 = 0. Ординаты этих точек соответственно равны 1; −2; 0; 13 ; 12 . Найти абсциссы этих точек.

27.Построить прямые, заданные следующими уравнениями:

150