
659
.pdf
Рассмотрим треугольник . Запишем проекцию отрезка ̅̅̅̅̅ на
направление нормали:
пр ̅̅̅̅̅ = | | cos .
Учитывая, что = − Θ, получаем:
пр ̅̅̅̅̅ = | | cos = | | cos( − Θ) =
=| |(cos cos + sin sin ) =
=(| | cos ) cos + (| | sin ) sin .
Рассмотрим треугольник . Выразим синус и косинус угла Θ че-
рез координаты точки :
sin = || || = | | , cos = || || = | | .
Отсюда:
= | | sin , = | | cos .
С учётом этих выражений получаем:
пр ̅̅̅̅̅ = cos + sin .
Учитывая, что пр ̅̅̅̅̅ = | | = , получаем:
= cos + sin
или
cos + sin − = 0,
где – угол наклона нормали к оси , – расстояние от начала координат до прямой. Полученное уравнение называется нормальным уравнением прямой.
Для приведения общего уравнения прямой + + = 0, где2 + 2 ≠ 0, к нормальному уравнению cos + sin − = 0, надо общее уравнение умножить на нормирующий множитель:
= ± |
1 |
, |
|
|
|
||
√ |
|
||
2+ 2 |
|||
где знак выбирается противоположным знаку коэффициента .
Пример. 3.28. Среди приведённых уравнений указать нормальные уравнения прямой:
1) = −3 + 5; |
2) 4 − 2 + 7 = 0; |
||||||||||||||
3) 4 − 2 − 7 = 0; |
4) |
3 |
− |
4 |
− 2 = 0; |
||||||||||
5 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
||||||
5) |
3 |
− |
4 |
|
+ 2 = 0; |
6) |
|
+ |
|
= 1; |
|||||
5 |
|
2 |
|
||||||||||||
|
|
5 |
|
|
|
3 |
|
|
|
||||||
7) |
5 |
+ |
12 |
− 1 = 0; |
8) − + 2 = 0; |
||||||||||
13 |
13 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
9) |
− 2 = 0; |
10) |
+ 1 = 0; |
||||||||||||
11) − 1 = 0; |
12) |
5 − 2 = 0. |
|||||||||||||
Решение. Нормальное уравнение прямой имеет вид cos +
+ sin − = 0. Это уравнение характеризуется тем, что коэффициенты при и по модулю не превосходят единицы (|cos | ≤ 1, |s | ≤ 1); сумма квадратов коэффициентов при и равна единице (по основному тригонометрическому тождеству cos2 + sin2 = 1); числовое слагаемое должно быть отрицательным.
1) = −3 + 5. Это уравнение является уравнением прямой с угловым коэффициентом.
111

2) 4 − 2 + 7 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое положительно: 7 > 0, поэтому уравнение не является нормальным.
3) 4 − 2 − 7 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое отрицательно: −7 < 0. Коэффициенты при неизвестных по модулю больше единицы: |4| > 1, |−2| > 1, поэтому уравнение не является нормальным.
4) 35 − 45 − 2 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое отрицательно: −2 < 0. Коэффициенты при неизвестных по модулю не превосходят единицы: |35| < 1, |− 45| < 1. Найдём сумму
квадратов коэффициентов при неизвестных: (35)2 + (− 45)2 = 259 + 1625 = 1.
Сумма квадратов равна единице. Все условия выполняются, поэтому уравнение является нормальным.
5) 35 − 45 + 2 = 0. В целом это уравнение имеет вид нормального.
Числовое слагаемое положительно: 2 > 0, поэтому уравнение не является нормальным.
6) 2 + 3 = 1. Это уравнение является уравнением прямой в отрезках.
7) 135 + 1213 − 1 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое отрицательно: −1 < 0. Коэффициенты при неизвестных по модулю не превосходят единицы: |135 | < 1, |1213| < 1. Найдём сумму
квадратов коэффициентов при неизвестных: (135 )2 + (1213)2 = 16925 + 144169 = 1. Сумма квадратов равна единице. Все условия выполняются, поэтому урав-
нение является нормальным.
8)− + 2 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое положительно: 2 > 0, поэтому уравнение не является нормальным.
9)− 2 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое отрицательно: −2 < 0. Коэффициенты при неизвестных по модулю не превосходят единицы: |1| = 1, |0| < 1. Найдём сумму квадратов коэффициентов при неизвестных: 12 + 02 = 1. Сумма квадратов равна единице. Все условия выполняются, поэтому уравнение является нормальным.
10)+ 1 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое положительно: 1 > 0, поэтому уравнение не является нормальным.
11)− 1 = 0. В целом это уравнение имеет вид нормального. Числовое слагаемое отрицательно: −1 < 0. Коэффициенты при неизвестных по модулю не превосходят единицы: |0| < 1, |1| = 1 Найдём сумму квадратов коэффициентов при неизвестных: 02 + 12 = 1. Сумма квадратов равна единице. Все условия выполняются, поэтому уравнение является нормальным.
12)5 − 2 = 0. В целом это уравнение имеет вид нормального. Коэффициенты при неизвестных по модулю больше единицы: |5| = 5 > 1, |−2| = 2 > 1, поэтому уравнение не является нормальным.
112

Ответ: 4, 7, 9, 11.
Пример. 3.29. Привести общее уравнение прямой к нормальному:
1) 4 − 3 + 6 = 0; |
2) 6 − 8 − 1 = 0; |
3) 2 + 3 − 3 = 0; |
4) + 5 = 0. |
Решение. Для приведения общего уравнения прямой к нормальному надо умножить общее уравнение на нормирующий множитель .
1) 4 − 3 + 6 = 0. Вычислим нормирующий множитель:
|
|
|
|
|
= − |
|
1 |
|
|
|
|
|
|
= − |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
+ |
2 |
|
√4 |
2 |
+(−3) |
2 |
5 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
Умножим уравнение на нормирующий множитель: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
− |
4 |
+ |
|
3 |
− |
6 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2) 6 − 8 − 1 = 0. Вычислим нормирующий множитель: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
= |
1 |
|
|
|
|
|
|
= |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
+ |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
√6 +(−8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
Умножим уравнение на нормирующий множитель: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
6 |
|
− |
8 |
− |
|
|
1 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
10 |
|
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
После преобразований: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
− |
4 |
− |
|
1 |
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
5 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3) |
2 + 3 − 3 = 0. Вычислим нормирующий множитель: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
= |
1 |
|
|
|
|
|
= |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
+ |
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
√13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
√2 +3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
Умножим уравнение на нормирующий множитель: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
+ |
3 |
|
|
− |
|
3 |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
√13 |
√13 |
√13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
4) + 5 = 0. Вычислим нормирующий множитель: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= − |
|
1 |
|
|
|
|
|
|
= − |
|
|
|
|
1 |
|
|
|
|
|
|
= −1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
+ |
2 |
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
√0 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
Умножим уравнение на нормирующий множитель: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
− − 5 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
Ответ: 1) − |
4 |
+ |
3 |
− |
6 |
= 0; 2) |
3 |
− |
4 |
− |
1 |
= 0; 3) |
|
2 |
+ |
3 |
− |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
5 |
10 |
|
√13 |
√13 |
|
||||||||||||||
− |
|
= 0; 4) − − 5 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
√13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.8. Угол между двумя прямыми
Пусть прямые 1 и 2 заданы уравнением с угловым коэффициентом:
= 1 + 1 и = 2 + 2 ,
где 1 = 1, 2 = 2; 1 и 2 – углы наклона прямых к оси . Обозначим через наименьший угол между прямыми 1 и 2
(рис. 3.40).
По чертежу запишем угол между прямыми через углы наклона прямых: = 2 − 1. Далее запишем тангенс угла между прямыми и воспользуемся формулой тангенса разности:
= ( 2 − 1) = 2− 1 .
1+ 1∙ 2
Учитывая, что 1 = 1, 2 = 2, получаем выражение тангенса угла между прямыми через угловые коэффициенты прямых:
113

2
1
2 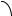 1
1
 1
1  2
2
|
|
Рис. 3.40. Угол между двумя прямыми, заданными уравнением с угловым коэффициентом
= 2−1 .
1+1∙2
По этой формуле находят угол между двумя прямыми.
Эта формула применима всегда, кроме случая = 2 , то есть когда
прямые перпендикулярны. В этом случае тангенс не существует, то есть
1 + 1 ∙ 2 = 0.
При нахождении угла между двумя прямыми обычно подразумевают острый угол. С учётом этого формулу можно записать в виде:
= | 2−1 |.
1+1∙2
В этом случае нет необходимости учитывать очерёдность прямых. Если есть необходимость учёта очерёдности прямых, то пользуются следующим правилом: поворот от первой прямой ко второй прямой должен происходить против часовой стрелки.
Выведем формулу угла между двумя прямыми, заданными общим уравнением. Пусть прямая 1 задана уравнением 1 + 1 + 1 = 0 и пря-
мая 2 задана уравнением 2 + 2 + 2 = 0. Преобразуем уравнение пер-
вой прямой к уравнению с угловым коэффициентом: = − 1 − 1 . Пре-
1 1
образуем уравнение второй прямой к уравнению с угловым коэффициен-
том: = − |
2 |
− |
2 |
|
. Угловой коэффициент первой прямой |
= − |
1 |
, уг- |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ловой коэффициент второй прямой 2 |
= − |
. Найдём угол между прямы- |
|||||||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ми: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
2 |
1 |
|
1 2− 2 1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
− |
|
− |
−(− ) |
|
− |
2 |
+ |
1 |
|
|
|
2 |
|
|
|
− |
|
|||||||||||||
|
|
|
2 |
1 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
2 |
|
2 |
1 |
|
||||||
= | |
|
|
|
| = | |
|
|
|
|
|
| = | |
|
|
|
|
| = | |
|
|
| = | |
|
|
|
|
|
|. |
|||||||||
1+1∙2 |
1+(− |
|
|
|
|
1+ |
|
1∙ |
|
+ |
2 |
1 2+ 1 2 |
|||||||||||||||||||||
|
|
|
|
|
1)∙(− |
2) |
|
|
|
|
2 |
1 2 |
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
2 |
|
1 2 |
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, угол между двумя прямыми, заданными общим уравнением, можно найти по формуле:
= | 1 2−2 1|.
1 2+ 1 2
114

Эта формула применима всегда, кроме случая = 2 , то есть когда
прямые перпендикулярны. В этом случае тангенс не существует, то есть
1 2 + 1 2 = 0.
Пример. 3.30. Найти угол между двумя прямыми:
1)= −3 + 7, = 2 + 1;
2)= 4 − 3, = 2 + 2;
3)= − 12 + 6, = − 13 − 43 .
Решение. Применим формулу нахождения угла между двумя пря-
мыми: = | 2− 1 |, где 1 – угловой коэффициент одной прямой, 2 –
1+ 1∙ 2
угловой коэффициент другой прямой.
В примере прямые заданы уравнением с угловым коэффициентом, поэтому коэффициенты перед " " – это и есть угловые коэффициенты прямых.
1) Выпишем угловые коэффициенты прямых: 1 = −3, 2 = 2. Под- |
||||||||||||||||||||||||||||||||||||||||||||
ставляем в формулу: |
= |
| |
|
2− 1 |
| = |
| |
2−(−3) |
| |
= |−1| = 1. |
Тогда |
угол |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1+ 1∙ 2 |
|
|
|
|
|
|
1+(−3)∙2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
между прямыми = 1 = |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) Выпишем угловые коэффициенты прямых: 1 = 4, |
2 = 2. Под- |
|||||||||||||||||||||||||||||||||||||||||||
ставляем в формулу: = | |
2− 1 |
| = |
| |
|
2−4 |
| = |− |
2 |
| = |
|
2 |
. Тогда угол между |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1+ 1∙ 2 |
|
|
1+4∙2 |
9 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
прямыми |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
||
3) Выпишем угловые коэффициенты прямых: = − |
|
, |
|
= − |
. |
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2− 1 |
|
|
|
−3−(−2) |
|
|
−3+2 |
|
|
6 |
|
1 |
|
|||||||||||||||||||
Подставляем в формулу: = | |
|
|
|
|
|
| |
= | |
|
|
|
| = | |
|
| = | |
|
| = |
|
. |
|||||||||||||||||||||||||||
1+ 1∙ 2 |
1+(−1)∙(−1) |
1+1 |
7 |
7 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
6 |
|
|
|
6 |
|
|
|
|
|
|
||||||||
Тогда угол между прямыми = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: 1) = |
|
; 2) = |
|
; 3) = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример. 3.31. Найти угол между двумя прямыми:
1)2 + − 5 = 0, 6 − 2 + 7 = 0;
2)− 3 + 6 = 0, 4 + 5 − 7 = 0;
3)6 − 7 − 2 = 0, 7 + 6 + 5 = 0
Решение. В примере прямые заданы общим уравнением + + + = 0. Найдём угол между прямыми двумя способами.
Первый способ. Применим формулу нахождения угла между двумя
прямыми: = | 2− 1 |, где 1 – угловой коэффициент одной прямой, 2 –
1+ 1∙ 2
угловой коэффициент другой прямой. Для нахождения угла между этими прямыми надо знать угловые коэффициенты прямых. Для этого преобразуем каждое уравнение к уравнению с угловым коэффициентом = + .
Второй способ. Применим формулу угла между двумя прямыми че-
рез коэффициенты общего уравнения: = | 1 2− 2 1| .
1 2+ 1 2
115

|
|
|
|
|
|
|
1) Первый способ. Преобразуем первое уравнение к уравнению с уг- |
|||||||||||||||||||||||||||||||||||||||||
ловым коэффициентом: = −2 + 5. Преобразуем второе уравнение: |
|
= |
||||||||||||||||||||||||||||||||||||||||||||||
3 + |
7 |
. |
Выпишем угловые коэффициенты |
прямых: |
|
= −2, |
|
|
= 3. |
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2− 1 |
|
|
|
3−(−2) |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Найдём угол между прямыми: = | |
| = | |
| |
= | |
|
|
|
| |
|
= |−1| = 1. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 1∙ 2 |
|
|
1+(−2)∙3 |
|
|
−5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Тогда угол между прямыми = 1 = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Второй способ. Подставляя значения коэффициентов общего урав- |
|||||||||||||||||||||||||||||||||||||||||
нения в формулу угла между двумя прямыми, получаем: = |
| |
2∙(−2)−6∙1 |
| = |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2∙6+1∙(−2) |
||||||||||
= | |
−10 |
| = |−1| = 1. Тогда угол между прямыми = 1 = |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
10 |
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2) Первый способ. Преобразуем первое уравнение к уравнению с уг- |
|||||||||||||||||||||||||||||||||||||||||
ловым коэффициентом: = |
1 |
+ 2. Преобразуем второе уравнение: |
|
= |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
7 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
4 |
|
|||||
− |
+ |
. Выпишем угловые коэффициенты |
|
прямых: |
= |
|
, |
|
|
= − |
. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
5 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2− 1 |
|
|
−54−31 |
|
−54−31 |
|
−1517 |
|||||||||||||||||||||||||
Найдём угол между прямыми: = | |
|
| = |
| |
|
|
| = | |
|
|
|
| = | |
|
|
|
| = |
|
|||||||||||||||||||||||||||||||||
1+ 1∙ 2 |
1+1∙(−4) |
1− |
4 |
|
|
11 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|||||||||
= |− |
17 |
| = |
17 |
. Тогда угол между прямыми = |
17 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
11 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Второй способ. Подставляя значения коэффициентов общего урав- |
|||||||||||||||||||||||||||||||||||||||||
нения в формулу угла между двумя прямыми, получаем: = |
| |
1∙5−4∙(−3) |
| = |
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1∙4+(−3)∙5 |
||||||||||
=|−1711| = |1711| = 1711 . Тогда угол между прямыми = 1711 .
3)Первый способ. Преобразуем первое уравнение к уравнению с уг-
ловым коэффициентом: = 67 − 27 . Преобразуем второе уравнение: =
− 76 − 56 . Выпишем угловые коэффициенты прямых: 1 = 67 , 2 = − 76 . Так
как 1 + 1 ∙ 2 =
= 1 + 67 ∙ (− 76) = 1 − 1 = 0, то не существует и = 2 .
Второй способ. Так как 1 2 + 1 2 = 6 ∙ 7 + (−7) ∙ 6 = 0, то не
существует и = 2 .
Ответ: 1) = 4 ; 2) = 1711 ; 3) = 2 .
Пример. 3.32. Даны вершины треугольника: (0; 2), (7; 3), (1; 6). Найти .
Решение. Выполним схематичный чертёж (рис. 3.41). Угол будем рассматривать как угол между прямыми и , причём прямую будем считать первой, прямую будем считать второй, так как вращение от к происходит против часовой стрелки.
Найдём угловые коэффициенты прямых:
|
|
|
− |
3−2 |
|
1 |
|
|
|
− |
|
|
6−2 |
|
||||
|
= |
|
|
= |
|
|
= |
|
|
, |
= |
|
|
= |
|
|
= 4. |
|
|
|
7−0 |
7 |
|
− |
|
1−0 |
|||||||||||
|
|
− |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Далее найдём угол между прямыми:
116
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.41. Нахождение угла треугольника (к Примеру 3.32) |
||||||||||||||||||||||
|
− |
|
|
− |
|
|
4−1 |
27 |
|
27 |
|
|
||||||||||
= |
2 |
1 |
= |
|
|
|
|
|
|
|
= |
|
7 |
|
= |
7 |
= |
|
|
. |
Тогда угол между |
|
1+ |
|
|
1+ |
|
|
∙ |
1 |
11 |
11 |
|||||||||||||
|
∙ |
|
|
|
|
|
1+7∙4 |
7 |
|
|
|
|||||||||||
|
1 |
2 |
|
27 |
|
|
|
|
|
|
|
|
|
|
||||||||
прямыми = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
11 |
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. |
3.33. Дана прямая |
2 + 3 + 4 = 0. |
Составить уравнение |
|||||||||||||||||||
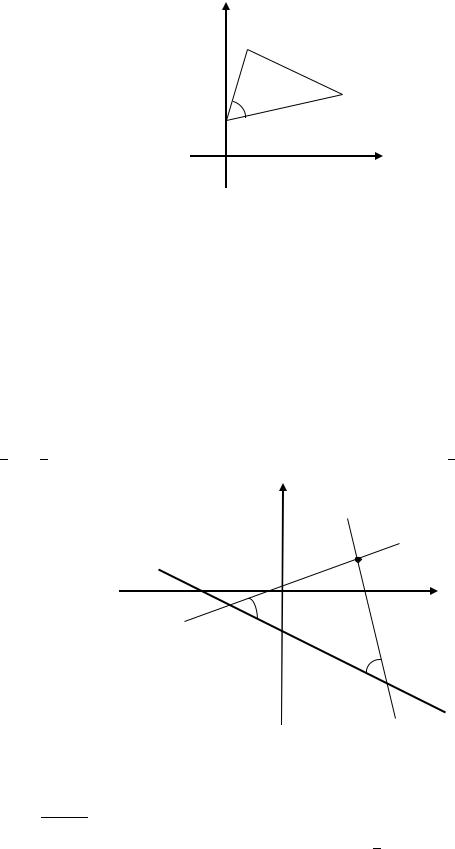
прямой, проходящей через точку 0(2; 1) под углом 450 к данной прямой. Решение. Возможны два варианта прохождения прямой. Выполним
схематичный чертёж (рис. 3.42). Обозначим угловой коэффициент искомой прямой через . Найдём угловой коэффициент искомой прямой. Для этого приведём уравнение прямой к уравнению с угловым коэффициентом: =
− 23 − 43 и тогда угловой коэффициент данной прямой 1 = − 23 .
|
0 |
450 |
|
|
450 |
Рис. 3.42. Составление уравнения прямой, проходящей под определённым углом к заданной прямой (к Примеру 3.33)
Далее применим формулу нахождения угла между двумя прямыми:
= | 2− 1 |, где 1 – угловой коэффициент одной прямой, 2 – угловой
1+ 1∙ 2
коэффициент другой прямой. Учитывая, что 1 = − 23 , 2 = , =
117

|
2 |
|
|
|
= 450 = 1, получаем: 1 = | |
+3 |
| . Преобразуем: | |
3 +2 |
| = 1. Распишем два |
2 |
|
|||
|
1− |
|
3−2 |
|
|
3 |
|
|
|
случая. |
|
|
|
|
1) 33−+22 = 1 . Из уравнения найдём :
3 + 2 = 3 − 2 ;
5 = 1;
= 15 .
Составим уравнение искомой прямой, используя уравнение прямой с данным угловым коэффициентом и проходящей через данную точку:
− 0 = ( − 0).
Получаем:
− 1 = 15 ( − 2).
Преобразуем к общему уравнению прямой:
5 − 5 = − 2;− 5 + 3 = 0.
2) 33−+22 = −1;
3 + 2 = −(3 − 2 ); 3 + 2 = −3 + 2 ;= −5.
Составим уравнение искомой прямой, используя уравнение прямой с данным угловым коэффициентом и проходящей через данную точку:
− 0 = ( − 0).
Получаем:
− 1 = −5( − 2).
Преобразуем к общему уравнению прямой:
− 1 = −5 + 10; 5 + − 11 = 0.
Ответ: − 5 + 3 = 0, 5 + − 11 = 0.
3.9. Взаимное расположение двух прямых на плоскости
Взаимное расположение двух прямых на плоскости, заданных уравнением с угловым коэффициентом.
Пусть прямые 1 и 2 заданы уравнением с угловым коэффициентом:
= 1 + 1 и = 2 + 2 , где 1 = 1, 2 = 2; 1 и 2 – уг-
лы наклона прямых к оси .
Если прямые параллельны, то 1 = 2 и, следовательно, 1 =
= 2, то есть 1 = 2 (рис. 3.43). Таким образом, равенство
1 = 2
является условием параллельности прямых.
118
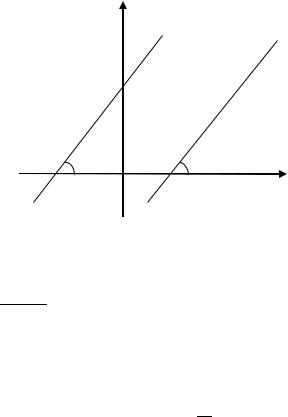
1 2
1 |
2 |
|
|
Рис. 3.43. Параллельные прямые, заданные уравнением с угловым коэффициентом
Если прямые перпендикулярны, то формула нахождения угла между
прямыми = 2− 1 теряет смысл, то есть 1 + 1 ∙ 2 = 0. Отсюда: 1 ∙
1+ 1∙ 2
2 = −1. Равенство
1 ∙ 2 = −1
является условием перпендикулярности прямых.
При решении ряда задач это равенство удобно переписать в виде:
2 = − 11 .
Эта формула позволяет находить угловой коэффициент прямой по известному угловому коэффициенту перпендикулярной ей прямой.
Если прямые совпадают, то выполняется условие параллельности1 = 2 и одновременно прямые отсекают равные отрезки на оси , то
есть 1 = 2. Таким образом, условие совпадения прямых принимает вид:
{ 1 = 2,1 = 2.
Взаимное расположение двух прямых на плоскости, заданных общим уравнением.
Пусть прямые 1 и 2 заданы общим уравнением:
1 + 1 + 1 = 0 и 2 + 2 + 2 = 0.
Приведём эти уравнения к уравнению с угловым коэффициентом, то есть к виду = + . Для этого в каждом уравнении выразим . Перенесём слагаемые 1 , 1 и 2 , 2 в правую часть:
1 = −1 − 1 и 2 = −2 − 2. |
|
|
|
|||||||||||||||||
Разделим первое уравнение на 1 ≠ 0, второе уравнение на 2 ≠ 0: |
||||||||||||||||||||
= − |
1 |
− |
1 |
и = − |
|
2 |
− |
2 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
1 |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|||||
Сравнивая полученные уравнения с уравнением = + , получа- |
||||||||||||||||||||
ем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
1 |
, = − |
1 |
, |
2 |
= − |
2 |
, = − |
2 |
. |
|
|||||||||
|
|
|
|
|
||||||||||||||||
1 |
|
1 |
1 |
|
1 |
|
|
2 |
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Учитывая условие параллельности прямых ( 1 |
= 2), заданных урав- |
|||||||||||||||||||
нением с угловым коэффициентом, получаем, что данные прямые парал-
119

лельны, если − |
1 |
= − |
2 |
или |
1 |
= |
2 |
. Преобразуем, разделив равенство на |
|||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
2 |
|
1 |
|
2 |
|
|
|
|
|
|
2 и умножив на 1. Получаем: |
|
|
1 |
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
= |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|||
Полученное равенство является условием параллельности прямых,
когда прямые заданы общим уравнением. Это условие означает, что прямые параллельны, если коэффициенты при неизвестных пропорциональны.
Учитывая условие перпендикулярности прямых ( 1 2 = −1), заданных уравнением с угловым коэффициентом, получаем, что данные прямые
перпендикулярны, если − |
1 |
∙ (− |
2 |
) = −1 или |
1 2 |
= −1. Преобразуем, |
||
|
|
|
||||||
|
|
|
|
|||||
|
1 |
|
2 |
|
1 |
2 |
|
|
умножив равенство на 1 2 и перенеся всё в левую часть. Получаем:
1 2 + 1 2 = 0.
Полученное равенство является условием перпендикулярности пря-
мых, когда прямые заданы общим уравнением. Это условие означает, что сумма произведений коэффициентов при и при равна нулю.
Учитывая условие совпадения прямых ( 1 = 2, 1 = 2), заданных уравнением с угловым коэффициентом, получаем, что данные прямые совпадают, если:
|
1 |
= |
1 |
и − |
1 |
= − |
2 |
. |
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
1 |
2 |
|
|||||||||
|
Преобразуем второе равенство, умножив его на −1, разделив на 2 и |
||||||||||||||
умножив на 1. Получаем: |
|||||||||||||||
|
|
|
1 |
= |
|
1 |
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
{ 2 |
|
|
2 |
|
|
|
||||||||
|
|
1 |
= |
|
|
1 |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||
Полученные условия можно записать одной формулой:
1 |
= |
1 |
= |
1 |
. |
|
|
|
|
|
|||
2 |
|
|
|
|||
|
2 |
2 |
|
|||
Полученное равенство является условием совпадения прямых, когда прямые заданы общим уравнением. Это условие означает, что прямые совпадают, если все коэффициенты пропорциональны.
Пример. 3.34. Дана прямая = −4 + 3. Определить угловой коэффициент прямой: а) параллельной данной прямой; б) перпендикулярной данной прямой.
Решение. Данная прямая задана уравнением с угловым коэффициентом = + , где – угловой коэффициент прямой. Для данной прямой
= −4.
а) Угловые коэффициенты параллельных прямых равны, поэтому угловой коэффициент искомой прямой также равен −4.
б) Угловые коэффициенты перпендикулярных прямых связаны ра-
венством ′ = − 1 , где ′ – угловой коэффициент искомой прямой, – угловой коэффициент данной прямой. Отсюда ′ = − 1 = − −14 = 14 .
Ответ: а) −4; б) 14 .
120
