
659
.pdf
Глава 2. Простейшие задачи аналитической геометрии на плоскости
В этой главе будет рассмотрен такой геометрический объект как точка, расположенная на плоскости. Такой точке ставится в соответствие пара чисел, называемых её координатами и определяющих её расположение на плоскости.
2.1. Система координат на плоскости
Для определения системы координат на плоскости (рис. 2.1) необхо-
димо:
1)выбрать две взаимно перпендикулярные прямые, одну из которых называют осью или осью абсцисс, другую называют осью или осью ординат; точку пересечения прямых называют началом координат; начало координат обозначают буквой , ось абсцисс – буквами , ось ординат – буквами ; оси и называют также осями координат;
2)на каждой оси координат задать положительное направление;
3)на каждой оси координат задать единицу масштаба (на чертеже – отрезок ).
Рис. 2.1. Декартова прямоугольная система координат на плоскости
Описанная система координат называется декартовой прямоугольной системой координат на плоскости.
2.2. Координаты точки на плоскости
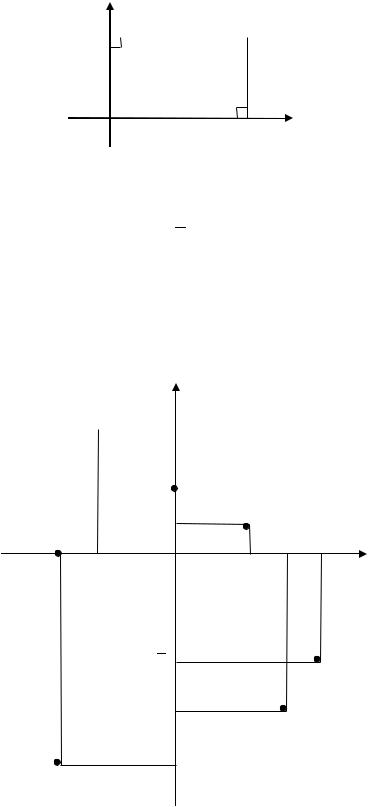
Рассмотрим произвольную точку и опустим из этой точки перпен-
дикуляры на оси координат. Основания перпендикуляров обозначим и |
||||
|
|
|
|
|
соответственно (рис. 2.2). |
|
|
|
|
|
|
|
|
|
Координатами точки в заданной системе координат называются |
||||
|
|
|
̅̅̅̅̅̅ |
|
числа = и = , где – величина отрезка |
, – вели- |
|||
|
|
|
|
|
̅̅̅̅̅̅ |
|
|
|
|
чина отрезка |
. Число называется абсциссой точки , число называ- |
|||
|
|
|
|
|
ется ординатой точки . Используют обозначение: |
(; ). |
|
||
|
|
21 |
|
|

|
|
|
|
|
|
Рис. 2.2. Координаты точки на плоскости |
||
Точки |
и называют проекциями точки на оси координат. |
||
|
|
|
|
Пример |
2.1. Построить точки (2; 1), |
(3; −5), |
(−2; 4), |
(−3; −7), (0; 2), (−3; 0), (4; −2√3).
Решение.
Для построения точки (2; 1) отложим по оси вправо отрезок длины 2. Получим точку – проекцию точки на ось . Далее отложим по оси вверх отрезок длины 1. Получим точку – проекцию точки на ось . Проведём через точки и прямые, параллельные осям координат. В пересечении этих прямых получаем точку (рис. 2.3).
 4
4
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
−3 −2 |
|
2 |
3 4 |
|
−2√3 |
|
|
|
|
|
−5 |
|
|
|
|
|
|
−7 |
|
|
Рис. 2.3. Построение точек , , , , , , (к Примеру 2.1)
Для построения точки (3; −5) отложим по оси вправо отрезок длины 3. Получим точку – проекцию точки на ось . Далее отложим по оси вниз отрезок длины 5. Получим точку – проекцию точки на
22
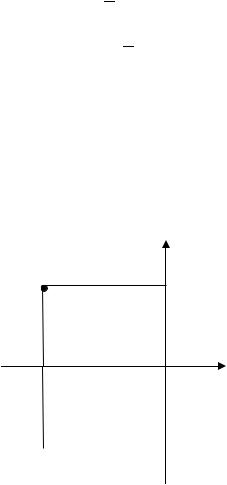
ось . Проведём через точки и прямые, параллельные осям координат. В пересечении этих прямых получаем точку (рис. 2.3).
Для построения точки (−2; 4) отложим по оси влево отрезок длины 2. Получим точку – проекцию точки С на ось . Далее отложим по оси вверх отрезок длины 4. Получим точку – проекцию точки С на ось . Проведём через точки и прямые, параллельные осям координат. В пересечении этих прямых получаем точку С (рис. 2.3).
Для построения точки (−3; −7) отложим по оси влево отрезок длины 3. Получим точку – проекцию точки на ось . Далее отложим по оси вниз отрезок длины 7. Получим точку – проекцию точки на ось . Проведём через точки и прямые, параллельные осям координат. В пересечении этих прямых получаем точку (рис. 2.3).
Для построения точки (0; 2) отложим по оси вверх отрезок длины 2. Получим точку – проекцию точки на ось . Проекция точки на ось равна нулю. Поэтому точка лежит на оси (рис. 2.3).
Для построения точки (−3; 0) отложим по оси влево отрезок длины 3. Получим точку – проекцию точки на ось . Проекция точки на ось равна нулю. Поэтому точка лежит на оси (рис. 2.3).
Для построения точки (4; −2√3) отложим по оси вправо отрезок длины 4. Получим точку – проекцию точки на ось . Далее отложим по оси вниз отрезок длины 2√3. Получим точку – проекцию точки на ось . Проведём через точки и прямые, параллельные осям координат. В пересечении этих прямых получаем точку (рис. 2.3).
Пример 2.2. Найти координаты точки, симметричной точке (−4; 3) относительно оси абсцисс.
Решение. Абсциссы точек, симметричных относительно оси абсцисс, совпадают, а ординаты отличаются знаком. Поэтому искомая точка имеет следующие координаты: ′(−4; −3). Нахождение точек, симметричных относительно чего-либо удобно определять графически (рис. 2.4).
|
|
|
3 |
|
−4 |
|
|
′  −3
−3
Рис. 2.4. Построение точки, симметричной относительно оси абсцисс (к Примеру 2.2)
23

Пример 2.3. Тело падает с высоты 50 метров под действием силы тяжести. Изобразить положение тела в тот момент, когда началось падение, когда оно закончилось, и промежуточные положения, вычисленные для каждой 0,5 секунды. Полученные точки соединить плавной кривой.
Указание. Путь, пройденный падающим телом без учёта сопротивле-
ния воздуха, вычисляют по формуле: = 22, где – время в секундах, –
ускорение свободного падения, ≈ 9,8 м/с2.
Решение. Обозначим через расстояние падающего тела до земли, при этом = 50 − . Будем изображать положение тела точками ( ; ). В начале падения = 0, = 0, = 50. Получаем точку, характеризующую положение тела в начале падения: 1(0; 50). В конце падения = 50, =
= 0, и тогда найдём из уравнения: 22 = 50. Отсюда = √10 ≈ √109,8 ≈ 3,2. Получаем точку, характеризующую положение тела в конце падения:
8(3,2; 0).
Найдём промежуточные точки.
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
При = 0,5: = |
∙(2) |
|
|
|
= |
|
≈ 1,2, = 50 − 1,2 = 48,8. Получаем точ- |
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|
8 |
|
||||||||||||||||||||||||||||||
ку 2(0,5; 48,8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
∙12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
При = 1: = |
= |
|
|
|
|
|
≈ 4,9, = 50 − 4,9 = 45,1. |
Получаем точку |
||||||||||||||||||||||||||||
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||
3(1; 45,1). |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
При = 1,5: |
= |
|
∙(2) |
|
|
|
|
= |
|
9 |
|
|
≈ 11,0, |
= 50 − 11,0 = 39,0. |
Получаем |
|||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
точку 4(1,5; 39,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
∙22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
При |
= 2: |
= |
|
= 2 ≈ 19,6, |
= 50 − 19,6 = 30,4. |
Получаем |
||||||||||||||||||||||||||||||
2 |
|
|
|||||||||||||||||||||||||||||||||||
точку 5(2; 30,4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
При = 2,5: = |
∙(2) |
|
= |
|
25 |
≈ 30,6, = 50 − 30,6 = 19,4. Получаем |
||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
точку 6(2,5; 19,4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∙32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
При = 3: = |
= |
|
|
9 |
≈ 44,1, = 50 − 44,1 = 5,9. Получаем точку |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
7(3; 5,9). |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Полученные результаты запишем в таблицу. |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
0 |
0,5 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1,5 |
|
2 |
2,5 |
|
3,0 |
|
3,2 |
|
||||||||||||
|
|
|
50 |
48,8 |
|
|
|
|
|
45,1 |
|
|
39,0 |
|
30,4 |
19,4 |
|
5,9 |
|
0 |
|
||||||||||||||||
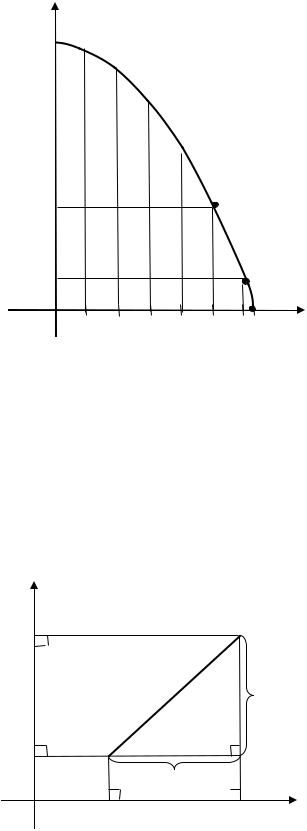
Отметим полученные точки и соединим их плавной линией (рис. 2.5).
24
50,0
48,8 

45,1 
39,0 
30,4 
19,4
5,9 |
|
|
|
|
|
|
|
0,5 |
1,0 |
1,5 |
2,0 |
2,5 3,0 3,2 |
|
Рис. 2.5. Точки, характеризующие падение тела под действием силы тяжести (к Примеру 2.3)
2.2. Расстояние между двумя точками на плоскости
Пусть 1( 1; 1) и 2( 2; 2) – две данные точки на плоскости. Найдём расстояние между ними. Для этого опустим из этих точек перпендикуляры на координатные оси. Основания перпендикуляров на оси обозначим 1 и 2 , на оси обозначим 1 и 2 (рис. 2.6). Через точку 1 проведём прямую, параллельную оси , через точку 2 проведём прямую, параллельную оси . Точку пересечения прямых обозначим через . Получаем прямоугольный треугольник 1 2 . Расстояние между точками 1 и 2 обозначим через .
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 − 1 |
|
1 |
1 |
|
|
|
|
|
|
||
|
2 |
− 1 |
|
|
|
1 |
|
2 |
|
|
||||
Рис. 2.6. Расстояние между двумя точками на плоскости
25
|
|
|
|
|
|
|
|
|
|
||||||||||
|
По теореме Пифагора = √ 2 + 2. При этом длина стороны |
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
̅̅̅̅̅̅ |
|
|
|
|
||
1 совпадает |
с абсолютной |
величиной отрезка |
то |
есть |
1 = |
||||||||||||||
1 , |
|||||||||||||||||||
| 2 − 1|; длина стороны 2 совпадает с абсолютной величиной отрезка |
|||||||||||||||||||
̅̅̅̅̅̅ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 , то есть 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= | |
− |. Тогда = √| |
− |
|2 + | |
− |
|2 = √( − )2 |
+ ( |
− )2. |
||||||||||||
2 |
1 |
2 |
1 |
|
2 |
1 |
|
|
|
|
2 |
|
1 |
2 |
1 |
|
|||
|
Таким образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
= √( − )2 + |
( − )2. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
1 |
|
2 |
|
|
1 |
|
|
|
|
|
||
Полученная формула означает, что расстояние между двумя точками равно квадратному корню из суммы квадратов разностей соответствующих координат точек.
Пример 2.4. Найти расстояние между точками 1(3; −6) и 2(1; 5). Решение. Воспользуемся формулой расстояния между двумя точка-
ми. Здесь 2 = 1, 1 = 3 , 2 = 5, 1 = −6. Получаем:
= √(1 − 3)2 + (5 − (−6))2 = √125 = 5√5.
Ответ: = 5√5.
Пример 2.5. Доказать, что треугольник с вершинами (1; 1), (2; 3),(5; −1) прямоугольный.
Решение. Треугольник является прямоугольным, если для него выполняется теорема Пифагора. Поэтому найдём квадраты длин сторон тре-
угольника по формуле расстояния между двумя точками:
2 = (2 − 1)2 + (3 − 1)2 = 5;2 = (5 − 2)2 + (−1 − 3)2 = 25;2 = (5 − 1)2 + (−1 − 1)2 = 20.
Получаем: 2 = 2 + 2. Значит треугольник прямоугольный. Пример 2.6. Даны две смежные вершины квадрата (2; −1),
(−1; 3). Определить две его другие вершины.
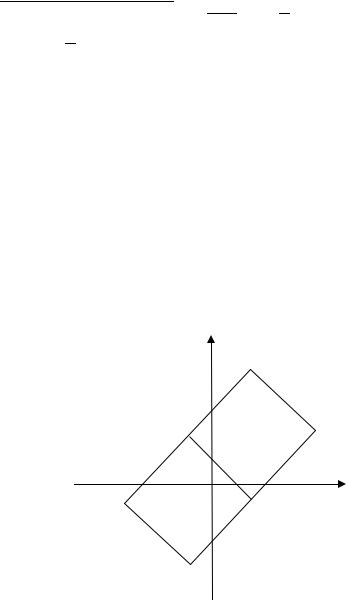
Решение. Со стороной возможны два квадрата. Обозначим их
1 1 и 2 2 (рис. 2.7).
|
|
|
|
2 |
|
|
|
2 |
|
|
|
1 |
|
1
Рис. 2.7. Два квадрата с общей стороной (к Примеру 2.6.)
26

1) Найдём координаты точек 1 и 2. Обозначим их координаты:
1( 1; 1) и 2( 2; 2).
С одной стороны:
12 = ( 1 + 1)2 + ( 1 − 3)2, 12 = ( 1 − 2)2 + ( 1 + 1)2,
с другой стороны:
12 = 2 = (−1 − 2)2 + (3 + 1)2 = 25,
По теореме Пифагора: 12 = 2 + 12 = 2 2 = 50.
Составим систему уравнений:
{( 1 + 1)2 + ( 1 − 3)2 = 25, ( 1 − 2)2 + ( 1 + 1)2 = 50.
Раскроем скобки:
{ 12 + 2 1 + 1 + 12 − 6 1 + 9 = 25,12 − 4 1 + 4 + 12 + 2 1 + 1 = 50.
Вычтем из первого уравнения второе:
6 1 − 8 1 = −30.
Выразим из полученного уравнения 1:
1 = 43 1 − 5.
Подставим полученное выражение во второе уравнение системы:
(43 1 − 5 − 2)2 + ( 1 + 1)2 = 50.
Преобразуем:
(4 1 − 21)2 + 9( 1 + 1)2 = 450.
16 12 − 168 1 + 441 + 9 12 + 18 1 + 9 − 450 = 0, 25 12 − 150 1 = 0,12 − 6 1 = 0,1 = 0, 2 = 6.
Тогда 1 = −5, 2 = 3.
Получаем следующие координаты точек: 1(−5; 0), 2(3; 6).
2) Найдём координаты точек 1 и 2. Обозначим их координаты:
1( 1; 1) и 2( 2; 2).
С одной стороны:
12 = ( 1 − 2)2 + ( 1 + 1)2, 12 = ( 1 + 1)2 + ( 1 − 3)2,
с другой стороны:
12 = 2 = 25, 12 = 2 + 12 = 2 2 = 50.
Составим систему уравнений:
{( 1 − 2)2 + ( 1 + 1)2 = 25, ( 1 + 1)2 + ( 1 − 3)2 = 50.
Раскроем скобки:
{ 12 − 4 1 + 4 + 12 + 2 1 + 1 = 25,12 + 2 1 + 1 + 12 − 6 1 + 9 = 50.
Вычтем из первого уравнения второе:
−6 1 + 8 1 = −20.
Выразим из полученного уравнения 1:
1 = 43 1 + 103 .
27

Подставим полученное выражение во второе уравнение системы:
(43 1 + 103 + 1)2 + ( 1 − 3)2 = 50.
Преобразуем:
(4 1 + 13)2 + 9( 1 − 3)2 = 450.
16 12 + 104 1 + 169 + 9 12 − 54 1 + 81 − 450 = 0, 25 12 + 50 1 − 200 = 0,12 + 2 1 − 8 = 0,1 = −4, 2 = 2.
Тогда 1 = −2, 2 = 6.
Получаем следующие координаты точек: 1(−2; −4), 2(6; 2).
Ответ: 1(−5; 0), 1(−2; −4) или 2(3; 6), 2(6; 2).
2.3. Проекция направленного отрезка на ось
Рассмотрим направленный отрезок ̅̅̅̅̅̅̅̅ и ось . Опустим из точек
1 2
1 и 2 перпендикуляры на ось . Основания перпендикуляров обозначим |
||||||
через 1 и 2 соответственно. |
|
̅̅̅̅̅̅̅̅ |
||||
Проекцией направленного отрезка 1 2 |
||||||
|
|
|
|
|
̅̅̅̅̅̅̅̅̅̅ |
|
на ось называется величина 1 2 направленного отрезка 1 2 , |
||||||
̅̅̅̅̅̅̅̅ |
|
|||||
(рис. 2.8). Обозначение: пр 1 |
2. Определение проекции в символьной |
|||||
̅̅̅̅̅̅̅̅ |
= 1 2 . |
|
||||
форме принимает вид: пр 1 2 |
|
|||||
|
|
|
|
2 |
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
|||||
|
||||||
Рис. 2.8. Проекция направленного отрезка на ось |
||||||
Пусть 1( 1; 1) и 2( 2; 2) – две данные точки плоскости. |
||||||
̅̅̅̅̅̅̅̅ |
на координатные оси. Найдём сначала про- |
|||||
Найдём проекции отрезка 1 2 |
||||||
екцию на ось . Для этого опустим из точек 1 и 2 перпендикуляры на ось . Основания перпендикуляров обозначим 1 и 2 соответственно
(рис. 2.9).
2
1
|
1 |
2 |
|
|
|
Рис. 2.9. Проекция направленного отрезка на ось
28
На оси точка 1 имеет координату 1, точка 2 имеет коорди-
нату 2 |
. Тогда величина 1 2 = 2 |
− 1, а значит: |
|
|
̅̅̅̅̅̅̅̅ |
= 2 − 1. |
|
|
пр 1 |
2 |
|
Таким образом, для нахождения абсциссы направленного отрезка надо от абсциссы его конца вычесть абсциссу его начала.
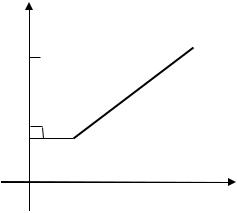
Далее найдём проекцию направленного отрезка на ось . Для этого опустим из точек 1 и 2 перпендикуляры на ось . Основания перпендикуляров обозначим 1 и 2 соответственно (рис. 2.10).
2  2
2
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.10. Проекция направленного отрезка на ось |
||
На оси точка 1 имеет координату 1, точка 2 имеет коорди- |
|||
нату 2 |
. Тогда величина 1 |
2 = 2 |
− 1, а значит: |
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
пр 1 |
2 = 2 − 1. |
Таким образом, для нахождения ординаты направленного отрезка |
|||
надо от ординаты его конца вычесть ординату его начала. |
|||
Пример 2.7. Даны точки 1(−2; 3) и 2(4; 5). Найти проекции от- |
||
̅̅̅̅̅̅̅̅ |
|
|
резка 1 2 на координатные оси. |
||
Решение. |
|
|
Найдём проекцию отрезка на ось , учитывая, что 2 = 4, 1 = −2: |
||
̅̅̅̅̅̅̅̅ |
= 2 − 1 |
= 4 − (−2) = 6. |
пр 1 2 |
||
Найдём проекцию отрезка на ось , учитывая, что 2 = 5, 1 = 3: |
||
̅̅̅̅̅̅̅̅ |
= 2 − 1 |
= 5 − 3 = 2. |
пр 1 2 |
||
|
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
Ответ: пр 1 2 = 6, пр 1 2 = 2. |
||
|
|
̅̅̅̅̅̅̅̅ |
Пример 2.8. Даны проекции отрезка 1 2 на координатные оси: |
||
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
|
пр 1 2 = 4, пр 1 2 = −5. Зная, что конец отрезка находится в точке |
||
2(1; −3), найти координаты его начала. |
|
Решение. Обозначим координаты начала отрезка через 1 |
и 1: |
1( 1; 1 ). |
|
̅̅̅̅̅̅̅̅ |
|
Запишем проекцию отрезка на ось : пр 1 2 = 2 − 1 = 1 − 1. |
|
̅̅̅̅̅̅̅̅ |
|
Учитывая, что по условию пр 1 2 = 4, получаем уравнение: 1 − 1 = 4. |
|
Отсюда 1 = −3. |
|
̅̅̅̅̅̅̅̅ |
|
Запишем проекцию отрезка на ось : пр 1 2 = 2 − 1 = −3 − |
|
̅̅̅̅̅̅̅̅ |
−3 − |
− 1. Учитывая, что по условию пр 1 2 = −5, получаем уравнение: |
|
1 = −5. Отсюда 1 = 2.
29
Таким образом, координаты начала отрезка: 1(−3; 2 ).
Ответ: 1(−3; 2 ).
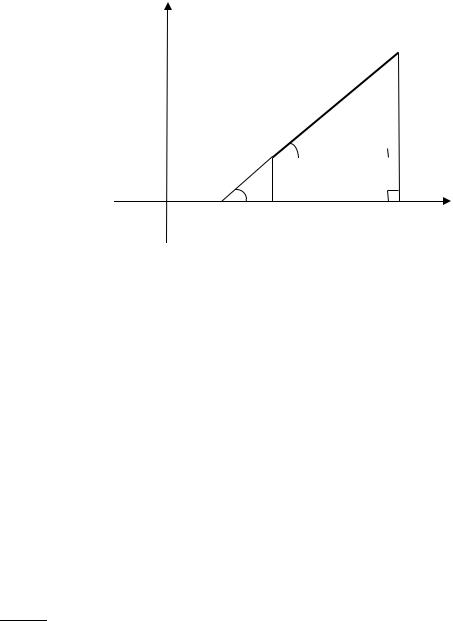
Выведем ещё одну формулу для вычисления проекции направленного отрезка на координатные оси. Найдём сначала проекцию на ось . Для
этого проведём через точку отрезок ̅̅̅̅̅̅ параллельно оси (рис. 2.11).
1 1
Обозначим через угол между отрезком ̅̅̅̅̅̅̅̅ и осью . Угол понима-
1 2
ют также как угол, на который надо повернуть ось до её совпадения с
̅̅̅̅̅̅̅̅ |
|
отрезком 1 2. Этот угол называют полярным углом отрезка. Тогда угол |
|
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅ |
между отрезками 1 2 |
и 1 также равен . При этом угол острый, если |
̅̅̅̅̅̅̅̅̅̅ |
|
направление отрезка 1 2 совпадает с направлением оси , и угол ту- |
|
|
̅̅̅̅̅̅̅̅̅̅ |
пой, если направление отрезка 1 2 противоположно направлению оси |
|
.
2
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
Рис. 2.11. Проекция направленного отрезка на ось |
|
|
|
||||||||||
Из прямоугольного треугольника : |
cos = |
1 |
= |
1 2 |
. |
||||||||
|
|
|
|||||||||||
|
|
1 |
2 |
|
|
|
| 1 2| |
|
| 1 2| |
||||
Учитывая определение проекции направленного отрезка на ось, величину
1 2 |
|
|
|
̅̅̅̅̅̅̅̅ |
|
можно записать следующим образом: 1 2 = пр 1 |
2. Тогда |
||||
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
cos = |
пр 1 2 |
|
. |
|
|
̅̅̅̅̅̅̅̅ |
|
|
|||
|
| 1 2| |
|
|
|
|
Отсюда: |
|
|
|
||
|
|
|
̅̅̅̅̅̅̅̅ |
= | 1 2| cos . |
|
|
|
|
пр 1 2 |
|
|
Таким образом, проекция направленного отрезка на ось равна произведению длины этого отрезка на косинус угла, образуемого отрезком
с осью . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
|
|
Далее найдём проекцию отрезка 1 2 на ось . Для этого проведём |
|||||||||
через точку 1 |
|
|
̅̅̅̅̅̅ |
(рис. 2.12). Обозначим че- |
||||||
отрезок 1 параллельно оси |
||||||||||
рез |
|
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
|
угол между отрезком 1 2 и осью . Тогда угол между отрезками |
||||||||||
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅ |
|
|
− . Это угол, образуемый отрезком с осью . |
|
|||||
1 2 |
и 1 равен |
2 |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
Из прямоугольного треугольника 1 2 |
: cos ( |
− ) = |
= |
||||||
|
2 |
| 1 2| |
||||||||
=1 2 . Учитывая определение проекции направленного отрезка на ось, | 1 2| 1 2 можно записать следующим образом: 1 2 =
30
