Пример. Сколькими способами 17 яблок можно разложить в 6 кучек по 2 яблока и одну кучку из 5-и яблок?

Решение. Требуется разбить множество из 17 яблок на непересекающиеся и неупорядоченные кучки. Откуда искомое число равно

□

Пример. Сколькими способами можно разделить колоду из 36 карт пополам так, чтобы в каждой пачке было по два туза?

Поясним это. Если бы нам надо было определить количество способов выбрать 2 туза из четырех, то мы бы имели C42 = 2!4!2! = 6 способов.

Перечислим эти варианты в левом столбце следующей таблицы, указав масти тузов, и в правом столбце укажем масти двух оставшихся тузов

В нашей задаче, например, первая и последняя строки представляют одно и то же разбиение, т.к. сейчас для нас не имеет значения в какую из двух групп попали тузы ♦ ♥ и ♣ ♠. Поэтому различных способов разделить 4 туза пополам в два раза меньше, т.е. всего 3.

Далее. Каждая половина любого из этих трех разбиений тузов играет роль различных двух «корзин», куда необходимо разложить пополам оставшиеся 32 карты. Разложение 32 оставшихся карт уже будет упорядоченным, так как «корзины» различные, число разложений равно

16!16!32! . Согласно правилу прямого произведения, общее число вариантов разделить колоду пополам равно 3 ×1632!16! !.

6.3 Бином Ньютона

Бином Ньютона. Рассмотрим разложение

Каждое слагаемое в разложении является результатом выбора а или b в каждом сомножителе (а + b) и последовательного их перемножения. Например, а5 получено путем выбора а из каждого сомножителя. Если из

17

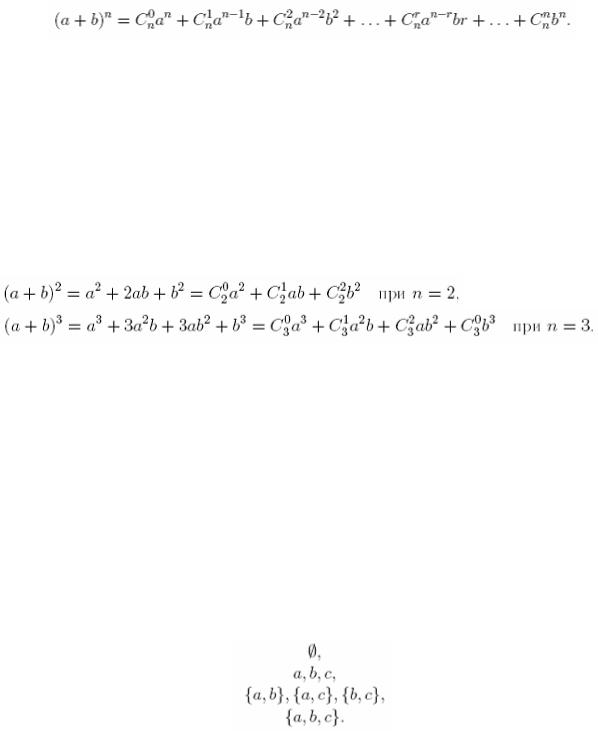
первого сомножителя выбрано а и b выбрано из остальных сомножителей, то в результате получим ab4. Предположим, что требуется найти коэффициент при a3b2. Слагаемое a3b2 получается при выборе трех а и двух b из пяти

сомножителей. Поскольку существует C53 способов выбора трех а, то коэффициент при a3b2 равен C53 . Обобщая результат, получаем следующую

теорему.

Биномиальная теорема. Для произвольного положительного целого числа n справедливы равенства

Доказательство. Поскольку arbn-r получено в результате r-кратного выбора а и n-r-кратного выбора b из n сомножителей в выражении (а + b)n, то коэффициент при arbn-r равен числу способов r-кратного выбора а из n

сомножителей Cnr . Второе равенство следует из того факта, что Cnr =Cnn−r .

□

Последняя формула известна под названием «бином Ньютона». Поскольку Cnr - это коэффициенты в биноме Ньютона, то числа Cnr еще называют

биномиальными коэффициентами.

Примерами бинома Ньютона при n=1,2,3 будут

(a + b)1 = a + b =C10 a1 + C11b1 при n=1

Пример. Покажем, что для любого положительного целого числа n

Все подмножества заданного n-элементного множества можно перечислить следующим образом. Вначале отмечаем пустое множество, потом перечисляем одноэлементные подмножества, потом перечисляем двухэлементные и т.д. Например, все подмножества множества {a,b,c} можно разместить следующим образом

18

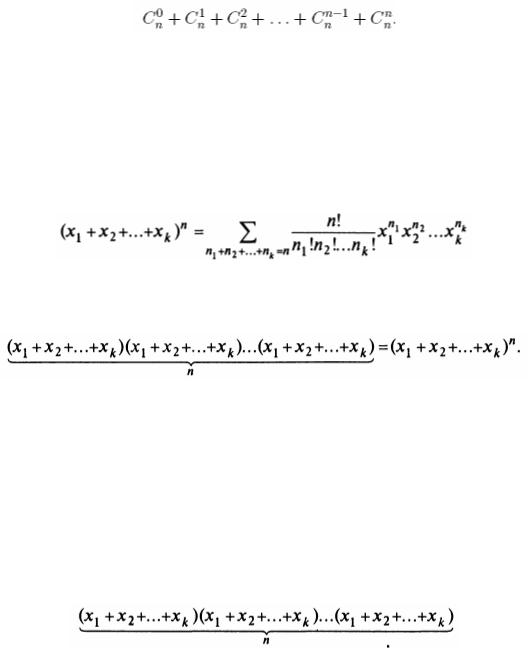
Напомним, что Cnk представляет количество способов выбрать k-элементное подмножество из n-элементного множества или, по-другому, количество различных k-элементных подмножеств. По правилу суммы количество подмножеств n-элементного множества равно

Используя результат предыдущего примера, получаем, что каждое n- элементное множество имеет 2n разных подмножеств.

n

Пример. Доказать тождество ∑Cnr (m −1)n−r = mn .

r=0

Воспользуемся формулой бинома Ньютона, где положим a=1 и b=m-1. □

Полиномиальная формула. Пусть слагаемых не два, а больше. Имеет место формула

Она называется полиномиальной, где суммирование выполняется по всем решениям уравнения n1 + n2 +... + nk = n в целых неотрицательных числах,

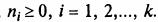Для доказательства выполним умножение

Чтобы привести подобные в полученном выражении, необходимо подсчитать

выбрать х1 в качестве множителя в n1 скобках при раскрытии выражения

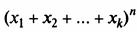. Это можно сделать Cnn1 способами. Из оставшихся n – n1 не раскрытых скобок необходимо выбрать х2 в качестве множителя в n2

повторениями.

□

Частный вид полиномиальной формулы, содержащий только два слагаемых,

n

(a + b)n = ∑Cnr ar bn−r называется биномом Ньютона.

r=0

19

Теорема. (Формула Паскаля). Для всех целых чисел r и n таких, что 1 ≤ r ≤ n имеет место

Доказательство. С одной стороны мы имеем По-другому

Приравнивая коэффициенты при an−r br в обеих формулах, убеждаемся в справедливости формулы (1).

□

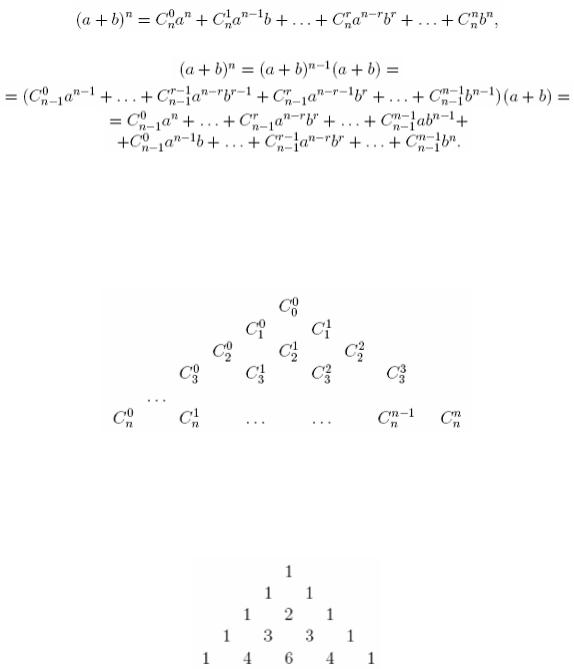
Формула (1) дает эффективный способ вычисления биномиальных коэффициентов. Запишем биномиальные коэффициенты в таблицу (она называется треугольником Паскаля)

Каждая (n+1)-я строка этого треугольника состоит из биномиальных коэффициентов, получающихся при раскрытии скобок в выражении (а + b)n. Так как Cn0 =Cnn =1, на внешних сторонах треугольника Паскаля всегда стоят единицы. Симметрия относительно вертикальной высоты треугольника следует из тождества Cnk =Cnn−k . Выпишем 5 строк треугольника Паскаля

Видим также, что каждое внутреннее число равно сумме двух верхних соседей. Это правило нами сформулировано в виде формулы Паскаля

Cnr =Cnr−−11 + Cnr−1 .

Формулу Паскаля можно доказать комбинаторно. Зафиксируем некоторый элемент n – элементного множества. Затем все r – элементные подмножества разобьем на два типа – к одному типу отнесем те подмножества, которые содержат выделенный элемент, а ко второму отнесем те подмножества, которые этот элемент не содержат. Ясно, что сумма количества первых и вторых подмножеств будет равна количеству r –

20