
DM_4
.pdf
Доля П.Г. Харьковский Национальный Университет механико – математический факультет кафедра геометрии им. А.В. Погорелова
Дискретная математика. |
|
Конспект лекций. |
|
Оглавление |
|
4. Отображения и функции. |
|
4.1 Понятие отображения.................................................................................... |
1 |
4.2. Композиция отображений и обратное отображение................................. |
5 |
4.3 Специальные виды отображений и функций.............................................. |
9 |
4.4 Принцип Дирихле. ....................................................................................... |
13 |
Упражнения........................................................................................................ |
15 |
4.1 Понятие отображения |
|
Пусть X и Y — произвольные непустые множества. Будем говорить, что |
|
определено отображение множества X в множество Y, если каждому |
|
элементу х множества X поставлен в соответствие некоторый вполне |
|
определенный элемент у множества Y. Этот элемент у называется образом |
|
элемента х при данном отображении. |
|
Отображение часто обозначают одной буквой (например, f), и тогда |
|
запись f : X →Y заменяет фразу «f — отображение |
множества X в |
множество Y». Образ элемента х при этом отображении обозначается символом f(x). Подчеркнем, что каждый x X имеет единственный образ f(x).
Отображение f : X →Y можно представлять себе как некое действие, которое переводит элементы х в их образы y = f (x) Y .
Примеры
1.Если каждому действительному числу х поставить в соответствие число x2, то тем самым будет определено отображение f : R → R (и даже в [0,+∞) ).
2.Пусть X=Y=R – множество действительных чисел. Формула y=2 x задает другое отображение R → R .
3.Пусть X – множество всех треугольников на плоскости, а Y – множество действительных чисел. Сопоставляя треугольнику его площадь, получаем отображение первого множества во второе.
1
3) Пусть X={1,2,3}, Y={2,3,4}. Множество пар |
|
G={(1,2),(2,2),(3,3)} |
|
задает отображение f, при котором f(1)=f(2)=2, f(3)=3. |
|
Понятия «функция» и «отображение» иногда отождествляют, пользуясь ими как синонимами. Все же чаще под функцией понимают отображение одного числового множества в другое.
Функции представляют из себя специальный тип бинарных отношений. По – другому, определение функции можно дать следующим образом. Функцией из множества А в множество В называется бинарное отношение, при котором каждый элемент множества А связан с единственным элементом множества В. Другими словами, для каждого a A существует ровно одна пара из отношения вида (а, b). В графических терминах функция описывается таким графом, у которого из каждой вершины, изображающей элементы множества A, выходит ровно одна стрелка.
Пример. Пусть А={-2,-1,0,1,2}, а В={0,1,2,3,4,5}. Определим отношение f A × B f={(-2,5),(-1,2),(0,1),(1,2),(2,5)}.
Отношение f — функция из A в В, так как f A × B , и каждый из элементов
А присутствует в качестве первой компоненты упорядоченной пары из f ровно один раз.
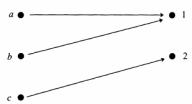
Пример. На рисунке изображен граф, представляющий функцию из множества {а,b,с} в {1,2}, состоящую из пар (а, 1), (b, 1) и (с, 2).
Пример. Определим, какие из следующих отношений между множествами А={а,b,с} и B={1,2,3} являются функциями из множества А в В.
(а) f={{а,1),(а,2),(b,3),(с,2)}; (б) g={{а,1),{b,2),(с,1)};
(в) h ={(а,1),(с,2)}.
Решение.
(а) Отношение f — не функция, поскольку элементу а соответствуют два разных элемента множества B : 1 и 2.
(б) Отношение g является функцией.
(в) Последнее отношение функцией не является, поскольку элементу b не соответствует ни одного элемента.
Пример. Определим, какие из следующих бинарных отношений между множествами А в В являются функциями.
(а) «x — брат или сестра у» на множестве всех людей;
2
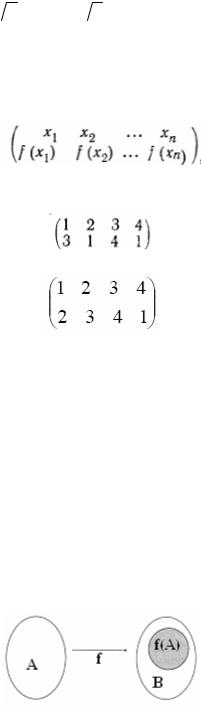
(б) отношение на множестве R, заданное парами: {{х,у):х=у2}
(а) Это не функция, поскольку есть люди с несколькими братьями и сестрами, а также бывают семьи с единственным ребенком.
(б) Последнее отношение — не функция, так как, например, обе упорядоченные пары: (2, 2) и (2,−
2) и (2,− 2) — ему принадлежат. Кроме того, в нем отсутствуют пары (x, у) с отрицательными x.
2) — ему принадлежат. Кроме того, в нем отсутствуют пары (x, у) с отрицательными x.
Пусть X ={x1,x2 ,..., xn } — конечное, а Y— произвольное множества. В этом случае отображение f : X →Y удобно задавать таблицей
где ниже элемента х из X указан его образ f(х). Так, если X={1,2,3,4}, то отображение f : X →Y с таблицей
переводит 1 в 3, 2 в 1, 3 в 4, 4 в 1. И например, таблица
задает отображение множества четвертей координатной плоскости в себя при повороте плоскости на 900. против часовой стрелки вокруг начала координат (вместо самих четвертей в этой таблице мы используем их номера).
Два отображения f : X →Y и g :U →V считаются равными, если X=U,
Y=V и для каждого элемента x множества X: f(x)=g(x).
Пусть f : X →Y . Множество f (X )={f (x): x X } образов всех элементов из X называется образом множества X при отображении f. Аналогично определяется образ любого подмножества А множества X:
f (A)={f (x): x A}.
Функцию, определенную на множестве А со значениями в множестве В удобно представить в виде диаграммы Эйлера.
f : A → B
Пусть y — фиксированный элемент из Y. Подмножество f −1(y)={x X : f (x)= y}
множества X, состоящее из всех тех x X , для которых y является образом при отображении f, называется полным прообразом элемента у при
3

отображении f. Каждый элемент из f-1(y) называют прообразом элемента у при отображении f. Может случиться, что f −1(y)= для некоторого y Y .
Если В — произвольное подмножество Y, то его полный прообраз определяется следующим образом
f −1(B)={x X : f (x) B}
Пример.
1.Рассмотрим отображение f:RÆR, где f(x)=х2 для любого x R . Тогда
2.Пусть А={-2,-1,0,1,2}, а В={0,1,2,3,4,5}. Функция f:АÆВ
определена соотношением f(x) = х2 + 1. Для } A , имеемE ={1, 2
f (E)={b :b = f (a) для некоторого a E}={2,5 }
является образом Е при отображении f. Если F ={0,2,3,4,5} B , то f −1(F )={b : a A f (a) =b }={−1,1,−2, 2 }
является прообразом F. Заметим, что элементы 0, 3 и 4 не вносят никаких элементов в f-1(F), поскольку они не принадлежат области значений функции f. Прообраз может быть пустым. Так, например, в случае W={0,3} прообраз f-l{W) пуст, поскольку не существует такого a A, для которого f(a) = 0 или f(а) = 3. Элементами f(A) являются те, и только те элементы области потенциальных значений B, которые используются функцией f.
Отображение f:XÆY называется инъективным или инъекцией, если для
любых x1,x2 X
x1 ≠ x2 f (x1 )≠ f (x2 )
Другими словами, f инъективно, если разные элементы множества X имеют разные образы при отображении f.
Отображение f:ХÆY называется сюръективным или сюръекцией, если f(X)=Y, т. е. если каждый элемент множества Y имеет хотя бы один прообраз.
Отображение, которое одновременно инъективно и сюръективно, называется биективным или биекцией. Часто биекцию называют взаимно однозначным отображением. Очевидно, f:ХÆY биективно тогда и только тогда, когда каждый элемент множества Y имеет точно один прообраз.
Пример. Пусть X={1,2,3}, Y={1,2}. Тогда отображение f : X →Y , где
сюрьективно, но не инъективно, а отображение g:YÆX, где
инъективно, но не сюръективно.
4

Пример. Рассмотрим функцию у = lg x. Ее область определения есть множество всех положительных действительных чисел. Поэтому она задает отображение f :(0, + ∞)→ R .
Легко понять, что f — биективное отображение.
Пусть задано отображение f : X →Y и A некоторое подмножество X. Тогда
можно рассмотреть отображение fA заданное на A: |
A →Y , определяемое |
равенством f A (x)= f (x) x A. Отображение fA |
называется сужением |
отображения f. |
|
Особенно часто встречаются отображения множеств в себя, т. е. отображения вида f:XÆX. Такие отображения называют преобразованиями множества X. Биективные преобразования f:XÆX называют подстановками множества X.
Преобразование Ix:XÆX, такое, что Iх(х)=х для любого x X , называется тождественным преобразованием множества X. Таким образом, Iх оставляет на месте каждый элемент из X. Часто вместо Iх пишут просто I, если из контекста ясно, какое множество X имеется в виду.
Множество X называется областью определения отображения f, а множество Y – областью значений. Множество упорядоченных пар
называют графиком отображения f. Непосредственно из определения вытекает, что график отображения f является подмножеством декартова произведения X x Y: Гf X ×Y .
4.2. Композиция отображений и обратное отображение
Пусть имеются два отображения вида f:ХÆY и g:YÆZ. Выберем произвольный элемент x X и применим к нему отображение f. Под действием f элемент х перейдет в элемент у=f(x) множества Y. Если теперь к элементу у применить отображение g, то у перейдет в элемент z=g(y) множества Z. В результате каждому x X ставится в соответствие вполне определенный элемент z=g(f(x)) множества Z. Таким образом, последовательное применение отображений f u g приводит к отображению
5
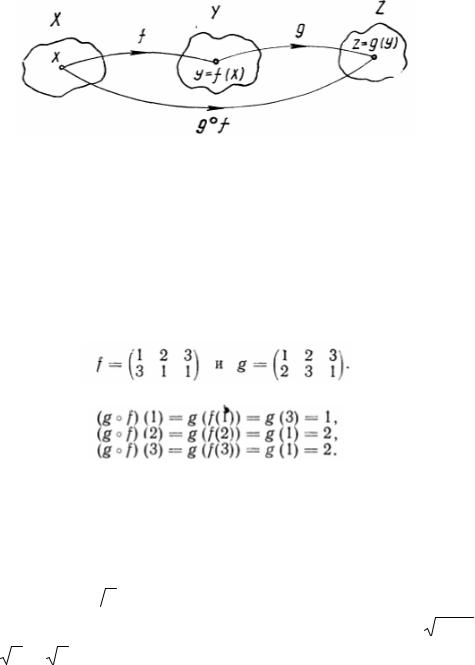
множества X в множество Z, которое называется произведением (или композицией) отображений g и f. Так как произведение отображений g и f переводит элемент x X в элемент g(f(x)), то это произведение естественно обозначать символом g о f или просто g f.
По определению (gоf)(х)=g(f(x)) для любого x X .
Отметим, что композиция отображений f:ХÆY и g:UÆV определено лишь в случае, когда U=Y. В частности, может оказаться, что gof определено, f o g не определено. Очевидно, если f u g — преобразования множества X, то определены оба произведения gof и fog. Они также являются преобразованиями X.
Пример. Пусть Х={1,2,3}. Рассмотрим следующие два преобразования множества X:
Тогда
Итак |
1 |
2 |
3 |
|
. Аналогично получаем, что |
f |
1 |
2 |
3 |
. Таким |
|
g o f = |
|
|
|
o g = |
|
|
|
||||
|
|
2 |
2 |
|
|
|
|
1 |
3 |
|
|
|
1 |
|
|
|
1 |
|
|
||||
образом, g o f ≠ f o g и, следовательно, композиция отображений, вообще говоря, зависит от порядка сомножителей.
Пример. Пусть f (x)=  x и g(x)= x + 5 - функции, заданные на множестве
x и g(x)= x + 5 - функции, заданные на множестве
действительных |
чисел. |
Имеем |
f (g(x))= f (x + 5)= x + 5 |
и |
||
g(f (x))= g( x )= x + 5 |
|
|
|
|||
Пример. |
Пусть |
f и g – преобразования множества R, соответствующие |
||||
функциям |
y =sin x и y = x2 , т.е. f (x)=sin x , g(x)= x2 x R . Композиции |
|||||
g o f |
и |
f o g |
определены |
и |
(g o f )(x)= g(f (x))= g(sin x)= (sin x)2 , |
|
(f o g)(x)= f (g(x))= f (x2 )=sin x2 . Очевидно g o f ≠ f o g . □
Отметим, что операция композиции преобразований множества R называется в математическом анализе суперпозицией функций, так что gof
— сложная функция, а под произведением функций понимается операция,
6

являющаяся обычным умножение действительных чисел, возвращаемых функциями.
Теорема. Пусть f, g, h —отображения, такие, что одно из произведений
(h o g )o f , h o(g o f )
определено. Тогда определено и другое произведение, причем
(h o g )o f = h o(g o f )
Доказательство. Пусть, например, определено h o(g o f ) (для какого – то
элемента x X ). Если f:XÆY, |
то g должно быть |
отображением вида |
|
g:YÆZ. Но тогда gof:XÆZ и, значит, h:ZÆU. |
Действительно, hog |
||
Проверим, что |
(h o g )o f |
тоже определено. |
|
определено и hog:YÆU Следовательно, определено |
и (h o g )o f причем |
||
(h o g )o f : X →U . |
|
|
|
Покажем теперь, что отображения (h o g )o f и h o(g o f ) равны, т. е.
для каждого x X
((h o g )o f )(x)= (h o(g o f ))(x)
Имеем
□
Опираясь на понятие произведения двух отображений, можно определить композицию трех, четырех и более отображений.
Пусть, например, f1,f2,…,fk – преобразования множества X. Их произведение определим индуктивно fk o(fk −1 o...(f3 o(f2 o f1 ))). Пользуясь
ассоциативностью умножения отображений, нетрудно доказать, что справедливо равенство
для любого 1≤i < k
Укажем еще несколько важных свойств композиции отображений.
Очевидно, третье свойство есть прямое следствие первых двух.
7
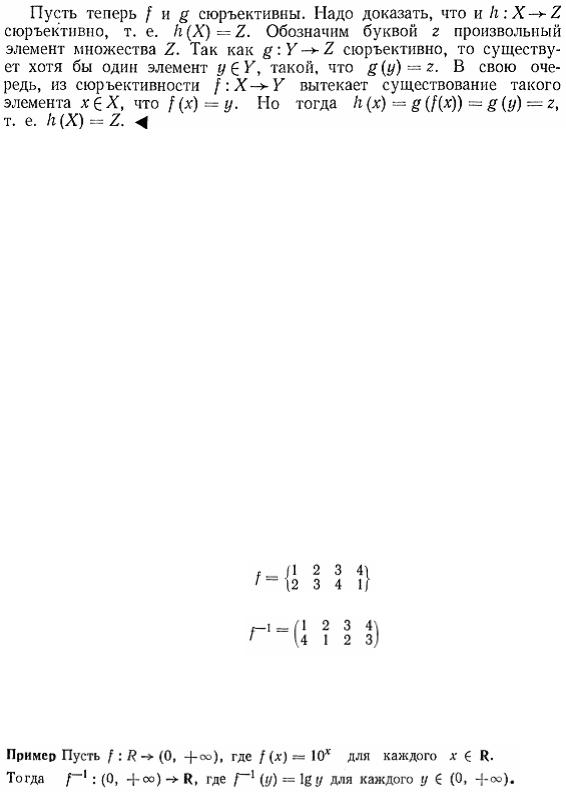
Теорема. Для тождественного отображения имеет место: если f : X →Y , то f o I X = f и IY o f = f .
Доказательство. Проверим, например, справедливость первого равенства. |
||
Для любого x X |
(f o I X )(x) = f (I X (x))= f (x) |
|
|
|
|
т. е. f o I X = f . Второе равенство проверяется аналогично. |
□ |
|
В случае, когда f — преобразование множества X, имеем f o I X = I X o f = f
Пусть f:ХÆY — биективное отображение. Тогда для любого элемента y Y
существует единственный элемент x X , такой, что f(x)=y. Отображение f-l:УÆХ, которое ставит в соответствие каждому y Y его прообраз x X
при отображении f, называется обратным к f. Таким образом, если f переводит х в у, то f-1 переводит у в х.
Инъективность и сюръективность отображения f-1 очевидны, и, следовательно, для любого биективного отображения обратное к нему тоже биективно. При этом (f-l)-l = f, т. е. обратное отображение к f-1 совпадает с f.
Пример. Пусть Х={1,2,3,4} и
есть подстановка множества X. Тогда
Действительно, так как f переводит 4 в 1, то f-1 переводит 1 в 4; f переводит 1 в 2 и, значит, f-1 переводит 2 в 1 и т. д.
Пример. Если f— поворот плоскости вокруг точки О на угол α , то f-l — поворот плоскости вокруг той же точки на угол −α .
Очевидно, определены композиции f −1 o f и f |
o f −1 , причем |
f −1 o f = I X , f o f −1 = IY |
(A) |
Действительно, f −1 o f : X → X x X и (f −1 o f )(x) = f −1(f (x))= x = I X (x).
Аналогично проверяется второе из равенств.
Следующая теорема показывает, что равенства (A) можно использовать в качестве определения обратного отображения.
8

т. е. y имеет по меньшей мере один прообраз g(y). Итак, f сюръективно, а поэтому и биективно.
Проверим, наконец, что g = f-l. Действительно, композиции
Пример. Требуется найти обратную функцию для у=З х+6. Обращая функцию, получаем
Но это то же самое, что (меняем буквы)
Решая уравнение относительно у, получаем
4.3 Специальные виды отображений и функций.
Пусть X — конечное множество, состоящее из n элементов. Эти элементы можно перенумеровать с помощью первых n натуральных чисел. Так как природа элементов множества X для нас не важна, то будем считать, что Х={1,2,...,n}. Всякое преобразование f множества X будем записывать так:
(1)
Если f — подстановка, т. е. биективное преобразование, то в строке f(1),f(2),...,f(n) выписаны все числа 1,2,...,n без повторений, только в другом порядке. Строки такого вида называются перестановками
9

из n чисел. Таким образом, перестановка из n чисел — это расположение чисел 1,2,...,n в некотором определенном порядке. Две перестановки из n чисел различаются порядком элементов, но не элементами (как множества они совпадают).
Пример. 1, 2, 3, 4; 3, 1, 2, 4; 4, 2, 1, 3 — различные перестановки из четырех чисел.
Итак, если f — подстановка множества X, то нижняя строка (1) есть некоторая перестановке из n чисел. Обратно, если a1, a2, … an — произвольная перестановка из n чисел, то преобразование
множества X является, очевидно, подстановкой. При этом различным перестановкам соответствуют различные подстановки.
Теорема. Количество различных перестановок из n чисел равно n! Доказательство проведем индукцией по n. При n=1 утверждение
теоремы очевидно. Будем считать, что n>1 и число различных перестановок из n–1 чисел равно (n– 1)!. Разобьем множество всех перестановок из n чисел на классы, состоящие из перестановок с одинаковым последним числом. Таких классов будет ровно n. Для фиксированного последнего элемента перестановок из первых n-1 элементов, по-предположению, равно (n-1)! Но тогда число всех перестановок из n чисел равно n(n– 1)!=n!.
□
Следствие. Число всех подстановок множества X из n элементов равно n!
Пример. Выпишем все перестановки из трех чисел:
1, 2, 3; 1, 3, 2; 2, 1, 3; 2, 3, 1; 3, 1, 2; 3, 2, 1.
Так как число различных перестановок из трех чисел равно 3! = 6, то других перестановок нет.
Приведем определения некоторых часто встречающихся функций. Напомним, что нам известна одна специальная функция —
тождественная функция I, определенная соотношением I(а) = а для всех a A. Она может быть представлена в виде
Функция f:АÆВ, где А — множество действительных чисел, а В — множество целых чисел, называется нижним округлением и обозначается f (x)= x , если она каждому a A ставит в соответствие наибольшее целое
число, меньшее или равное а. Функция f:FÆВ называется верхним округлением и обозначается f (x)= x , если она каждому a A ставит в соответствие наименьшее целое число, большее или равное а.
10
