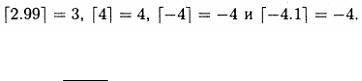
Вместо функции нижнего округления часто говорят о целой части числа. Функция, называемая целой частью числа, сопоставляет вещественному числу x наибольшее целое число, не превосходящее x, и обозначается так: [х].

Пример. [2.99]=2, [4]=4, [-4]=-4, [-4.1]=-5. Точно также

Пример. Пусть A={-1,0,1,2} и функция f : A → Z определяется формулой:

f(x)= x2 +1 . Тогда ее множество значений {0,1}/

3

Пусть А и В совпадают со множеством неотрицательных целых чисел. Факториалом называют функцию f:А—>В, обозначаемую через f (n)= n! и

определяемую следующими соотношениями:

0! = 1 1! = 1 =1·0!

2! = 1·2 =2=2·1! 3! = 1·2·3 =6 =3·2!

4! = 1·2·3·4 = 24 = 4-3!

. . . . . . . . . .

k! = 1·2·3·4·…·k = k·(k-l)!

Конечной последовательностью называют функцию из {1,2,3,4,...,n} в некоторое множество S. Бесконечной последовательностью назовем функцию из {1,2,3,4,...} в некоторое множество S. Любая конечная или бесконечная последовательность может быть названа просто последовательностью.

В большинстве случаев S представляет собой множество положительных целых, целых, рациональных или действительных чисел. Последовательность обычно изображают списком или перечислением элементов. Если А — функция, то значение А(1) можно обозначить через А1, значение А(2) — через А2 и так далее. Например, последовательности

1,4,9,16,... соответствует запись Ai =i2 . Здесь А(1)=1,А(2)=4,А(3)=9,

А(4)=16 и т.д. Заметьте, что 1,4,9,16 и 1,9,4,16 - это две разные последовательности.

Пример. Заданы первые пять членов последовательности: 0,3,8,15,24. Требуется описать ее как функцию. Легко видеть, что А(n)=n2-1.

Два вида последовательностей — арифметическая прогрессия и геометрическая прогрессия — представляют особый интерес. Каждый член арифметической прогрессии может быть получен из предыдущего прибавлением константы с. Таким образом, арифметическая прогрессия имеет вид A(n)=а+ (n-1) с, где а — первый член прогрессии. Например,

11

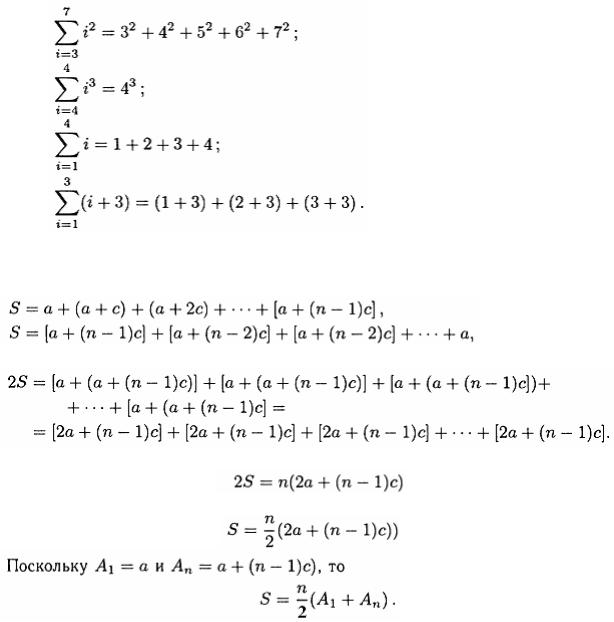
последовательность 3, 5, 7, 9, 11, ... представляет собой арифметическую прогрессию с а=3 и с=2.

В геометрической прогрессии каждый член может быть получен из предыдущего путем умножения на константу r. Таким образом,

геометрическая прогрессия имеет вид A(n) = a r n−1, где а — первый член

прогрессии. Последовательность 4, 12, 36, 108, 324, ... является геометрической прогрессией, в которой а = 4 и r = 3. Последовательность 32, 16, 8, 4, 2, ... — геометрическая прогрессия, где а = 32 и r =1/2.

Для суммирования членов последовательности

r+k

Ar + Ar+1 + Ar+2 +... + Ar+k используется специальное обозначение ∑Ai .

i=r

Например

Выведем формулу суммы первых n членов арифметической прогрессии. Запишем сумму первых n членов арифметической прогрессии в прямом и обратном порядке

и сложим

Таким образом, имеем

так что

□

Характеристические функции. Пусть X – некоторое множество, и A – его подмножество. Определим отображение χA множества X в двухэлементное множество {0,1} следующим образом: χA (x)=1, если x A, и χA (x)= 0, если

12

x A . Функция χA называется характеристической функцией подмножества A. Очевидно, A B тогда и только тогда, когда χA (x)≤ χB (x) для всех x.

Имеется простая связь между операциями над подмножествами множества X и операциями над их характеристическими функциями:

4.4 Принцип Дирихле.

Пусть f : А —> В — функция, причем как A, так и В — конечные множества. Предположим, что А состоит из п элементов: a1, а2,…an. Принцип Дирихле гласит, что если |А| > |В|, то по крайней мере одно значение f встретится

более одного раза. Проще говоря, найдется пара элементов ai ≠ a j , для

которых f (ai )= f (a j ).

Допуская некоторую вольность, принцип Дирихле можно переформулировать в легко запоминающейся форме: нельзя рассадить 10 зайцев в 9 клеток так, чтобы в каждой клетке сидел один заяц.

Чтобы убедиться в истинности принципа, предположим, что для любой пары разных индексов i ≠ j мы имеем f (ai )≠ f (a j ). Тогда множество В

содержит по крайней мере n различных элементов: f (a1 ), f (an ),..., f (an ). И уж во всяком случае B ≥ n , что противоречит предположению n = A > B . Следовательно, есть хотя бы два разных элемента ai ,a j A, для которых

f (ai )= f (a j ).

Пример 1. В автобусе едет 15 людей. Покажем что, по крайней мере, у двоих из них день рождения в одном и том же месяце.

Решение. Множество людей в автобусе обозначим буквой А, а множество всех 12 месяцев обозначим через В. Рассмотрим функцию f:А—>B, сопоставляющую каждому человеку из автобуса месяц его рождения. Так как A =15, а B =12, то A > B . По принципу Дирихле функция f должна иметь

повторяющиеся значения, т. е. найдутся два человека с одним и тем же месяцем рождения.

Для данной задачи трудно понять, зачем нам применять формальное рассуждение. Действительно. Дано 15 человек и 12 месяцев. Поэтому совершенно очевидно, что хотя бы двое из них родились в один и тот же месяц. Но в более сложных задачах применение принципа является полезным.

Пример 2. Какое наименьшее число фамилий должно быть записано в телефонном справочнике, чтобы с гарантией можно было утверждать, что

13

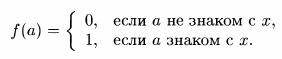
хотя бы две фамилии начинаются с одной и той же буквы и заканчиваются одинаковыми буквами?

Решение. Пусть А — множество фамилий в справочнике, а B — множество пар букв, выписанных из стандартного алфавита русского языка, насчитывающего 33 буквы. Обозначим через f:А—>В функцию, которая каждой фамилии справочника ставит в соответствие пару букв: первую и последнюю буквы фамилии. Например, f(Кузнецов)Æ(к,в). Множество В содержит 33*33 = 1089 пар букв. Принцип Дирихле гарантирует нам, что если |А| > |В| = 1089, то найдется по крайней мере две фамилии, начинающиеся и оканчивающиеся на одинаковые буквы. Поэтому телефонный справочник должен содержать не менее 1090 фамилий.

Пример 3. Покажите, что какие бы пять цифр из 1, 2, 3, 4, 5, 6, 7 и 8 мы ни выбрали, найдутся хотя бы две из них, сумма которых равна 9.

Решение. Перечислим пары цифр, дающих в сумме 9: {1,8},{2,7}, {3,6},{4,5}. Обозначим через А множество выбранных пяти цифр (не важно каких конкретно), а через В множество пар:

B={{1,8},{2,7},{3,6},{4,5}}.

Рассмотрим функцию f:А—>В, сопоставляющую каждой цифре из пятерки пару из множества B, которая в ней содержится. Например, f(3)={3,6}. По принципу Дирихле хотя бы две цифры из множества А попадут в одну и ту же пару. Короче говоря, две из пяти цифр дадут в сумме 9.

Пример 4. Покажите, что в любой группе из шести человек найдутся трое, знакомые друг с другом, или наоборот, совершенно не знающие друг друга. Решение. Пусть х — один из шести людей, А — множество оставшихся пяти людей в группе и В={0, 1}. Определим функцию f:А—>В по правилу:

Среди значений такой функции, очевидно, будет три или больше единиц, или три или больше нулей. Т.е. найдется три человека, которые либо все знакомы с x, либо все трое его не знают.

Предположим теперь, что три человека а, b и с знакомы с х. Если все три друг с другом не знакомы, то мы получаем решение задачи. В противном случае, какая-то пара, скажем а и b знает друг друга. Но они же знакомы и с х. Стало быть, трое людей: а, b и х — хорошие знакомые. Аналогично разбирается случай, когда нашлась тройка людей, которые с x не знакомы.

14

Упражнения

Упражнения к п. 4.1.

7. Определите, какие из отображений, задаваемых с помощью перечисленных ниже функций, инъективны, сюръективны, биективны:

9. Докажите, что если X — конечное множество, то инъективность отображения f:XÆX равносильна его сюръективности.

15