
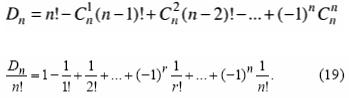
{1,2,3} являются (3,1,2) и (2,3,1). Перечислим беспорядки из четырех элементов:
2143; 2341; 2413; 3142; 3412; 3421; 4123; 4312; 4321.
Значит, D4 = 9.
Если перестановке назначить свойство – один предмет остается на своем месте, то таких перестановок будет Cn1 (n −1)!, поскольку предмет может находиться на любом из Cn1 месте, а остальные элементы можно переставить (n −1)! способами. Аналогично, перестановок в которых два предмета остаются на своем месте будет Cn2 (n − 2)! и т.д. Подставляя это в (3) приходим к
Последнее равенство можно переписать следующим образом:
Также ясно, что количество перестановок n различных предметов, при которых ровно k предметов стоят на своих первоначальных местах, выражается числом Dn,k =Cnk Dn−k .
6.5 Метод рекуррентных соотношений
Последовательность a0,a1,a2,… называют рекуррентной, если указана зависимость общего члена последовательности от предыдущих и заданы значения необходимого числа начальных членов.
Примерами рекуррентных последовательностей могут служить арифметические и геометрические прогрессии.
Члены геометрической прогрессии a0, a1, a2,… со знаменателем q поопределению связаны рекуррентным соотношением
an+1=q an.
и для однозначного ее определения надо задать начальное значение a0. Члены произвольной арифметической прогрессии a0, a1, a2,… связаны
рекуррентным соотношением an+1 = an + или, например, соотношением
an+2 = 2an+1 – an.
Действительно |
|
|
|
|
an = a0 + (n −1) |
|
|
|
|
an+1 = a0 + n |
|
)− (a0 + (n −1) )= 2 an+1 − an |
||
an+2 = a0 + (n +1) = 2(a0 + n |
||||
Последовательность |
факториалов |
1,2,6,…,n!,… |
определяется |
|
рекуррентным соотношением |
|
|
|
|
|
an+1=(n+1)an |
|
||
с заданием начального значения a0 |
= 1. |
|
|
|
Как рекуррентость может трактоваться формула
25
связывающая биномиальные коэффициенты.
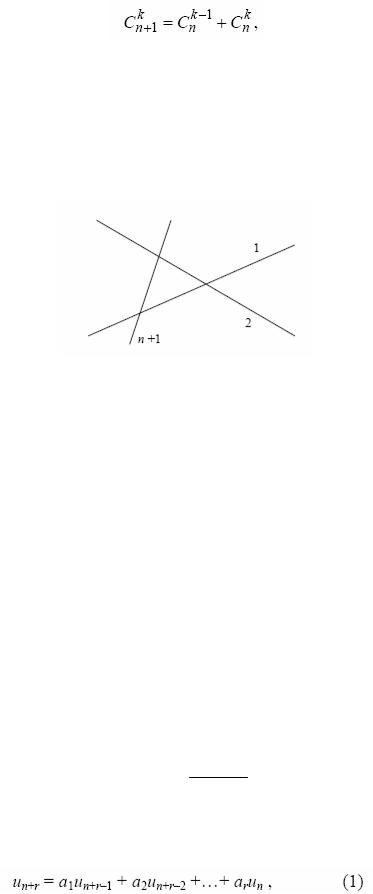
Пример. Рассмотрим задачу о разбиении плоскости прямыми. Пусть Dn – число областей, на которые разбивают плоскость n прямых общего положения (таких, что никакие три из них не пересекаются в общей точке и никакие две прямые не параллельны). Ясно, что D0 = 1, D1 = 2. Предположим, что на плоскости уже проведено n прямых, и посмотрим, сколько новых областей добавляется при проведении «новой» n+1-й прямой.
Каждую область, по которой проходит эта прямая, она рассекает на две. Таким образом, общее число областей увеличится на число областей, через которые проходит n+1-я прямая. Двигаясь по n+1-й прямой в одном направлении, мы пересечем границы областей n раз по числу «старых» прямых. Значит, n+1-я прямая пройдет через n+1 область (в последовательности область – граница – … – область – граница – область, число областей на единицу больше, чем число границ). В результате получаем рекуррентное соотношение
Dn+1=Dn+(n+1).
Чтобы найти замкнутое выражение для членов последовательности Dn, просуммируем следующие равенства:
D1 = D0 + 1;
D2 = D1 + 2;
………………
Dn = Dn–1 + n .
После сокращений получаем
Dn = D0 + 1 + 2 +…+n .
Следовательно,
Dn =1 + n(n2+1)
□
Рекуррентная последовательность u0,u1,u2,… называется линейной однородной, если ее члены связаны соотношением вида
где ai, i=1,2,…,r, – постоянные, не зависящие от n. Соотношение (1) называется линейным однородным рекуррентным уравнением порядка r.
26
Пример. Уравнение первого порядка с постоянными коэффициентами имеет вид
yn − a yn−1 = 0 и задается начальное значение y0 |
= y0 . |
(2) |
|||||||
Последовательные вычисления дают |
|
=K= an y = an y0 |
|
|
|||||
y |
n |
= a y |
n−1 |
= a a y |
n−2 |
. |
|
||
|
|
|
|
0 |
|
||||
Т.о. геометрическая |
прогрессия y0 an |
является решением |
линейного |
||||||
однородного рекуррентного уравнения первого порядка. |
|
□ |
|||||||
|
|
|
|
|
|
|
|
|
|
Пример. Уравнение первого порядка с переменными коэффициентами имеет
вид yn+1 − an yn |
= 0 с начальным значением y0 = y0 . Тогда |
|||||||||||||||||
|
|
|
y1 = a0 y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y2 = a1 y1 = a1a0 y0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y3 = a2 y2 = a2 a1a0 y0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
. . . |
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn = an−1 La2 a1a0 y0 = y0 ∏ak |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
где использовано обозначение ∏kn=0 ak = a0 a1 a2 ... an . |
||||||||||||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
□ |
||
Линейное |
неоднородное |
уравнение 1-го порядка имеет вид |
||||||||||||||||
yn+1 − a yn = fn , |
для |
которого |
надо |
задать |
начальное значение y0 = y0 и |
|||||||||||||
последовательность значений |
fn . Имеем |
|
|
|
|
|
||||||||||||
y1 = a y0 + f1 |
= a(a y |
|
|
) |
|
|
|
|
+(af + f |
|
) |
|||||||
y |
2 |
= a y + f |
2 |
0 |
+ f |
+ f |
2 |
= a2 y |
0 |
2 |
||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
||||||
y3 = a y2 + f3 = a(a2 y0 +(af1 + f2 ))+ f3 = a3 y0 +(a2 f1 + af2 + f3 ) |
||||||||||||||||||
Ясно, что |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn = an y0 + ∑an−k fk |
|
|
|
|
(3) |
||||||
k =1
Здесь мы имеем сумму решения однородного уравнения (2) и некоторого
n
частного решения неоднородного уравнения zn = ∑an−k fk . Действительно
k =1
zn −a zn−1 =(an−1 f1 + an−2 f2 +K+ afn−1 + fn )− −a(an−2 f1 + an−3 f2 +K+ afn−2 + fn−1 )= fn
□
Пример. Требуется подсчитать количество двоичных слов длины n, в которых единицы не могут стоять на соседних местах. Будем называть такие слова правильными и обозначим через An число правильных слов длины n.
Разобьем множество правильных слов длины n на два класса: слова оканчивающиеся на ноль и слова, оканчивающиеся на единицу. Количество
27
слов в этих классах обозначим An(0) и An(1) соответственно. Очевидно, что An = An(0) + An(1). У слова, оканчивающегося на ноль первые n-1 символов образуют правильное слово длины n-1. Следовательно An(0) = An−1 . Если
правильное слово длины n оканчивается на единицу, то предыдущий символ этого слова должен быть нулем, а первые n-2 символа будут образовывать
правильное слово длины n-2. Поэтому An(1) = An−2 . В результате мы имеем
соотношение
An = An−1 + An−2
Как видим, решение нашей задачи свелось к рекуррентному уравнению. В переводе – возвратному, так как для подсчета интересующей нас величины для некоторого n нужно возвратиться к предыдущим значениям этой
величины. Здесь легко видеть, что A1 = 2 и A2 = 2 . Поэтому |
A3 = 2 + 2 = 4 , |
|
A4 = 2 + 4 = 6 и т.д. |
□ |
|
В общем случае рекуррентное соотношение имеет вид |
||
|
||
an = F (an−1 ,an−2 ,..., an−k ) |
(4) |
|
Как правило, мы будем иметь дело с уравнением вида |
(5) |
|
an = c1an−1 + c2 an−2 +... + ck an−k |
где c1 ,c2 ,...,ck - заданные числа. Такое соотношение называют линейным
рекуррентным уравнением k – го порядка с постоянными коэффициентами. Соотношение (4) или (5) мы будем рассматривать как уравнение относительно неизвестной функции A(n)=An и каждую последовательность
~ = ( )
A A0 , A1 ,..., An ,...
для которой выполняется соотношение (4) или (5) будем называть решением рекуррентного соотношения.
Лемма 1. |
Если последовательность |
~ |
,..., An ,...) является решением |
A = (A0 , A1 |
|||
рекуррентного соотношения (5) и C любое число, то и последовательность |
|||
~ |
,CA1 ,...,CAn ,...) также |
является |
решением рекуррентного |
CA = (CA0 |
|||
соотношения (5).
Доказательство. Подставив вторую последовательность в (5) и поделив на C , убеждаемся, что и вторая последовательность является решением. Если
~
же C=0, то последовательность C A состоит из одних нулей и, очевидно, также удовлетворяет соотношению (5).
~ |
|
|
□ |
|
|
~ |
|
Лемма 2. Если A = |
(A0 , A1 ,..., An ,...) B =(B0 , B1 ,..., Bn ,...) являются решениями |
||
рекуррентного соотношения (5), то последовательность |
|||
~ |
~ |
~ |
+ B0 , A1 + B1 ,..., An + Bn ,...) |
C |
= A + B = (A0 |
||
также является решением рекуррентного соотношения (5). |
|||
|
|
~ |
~ |
Доказательство. Так как A и |
B являются решениями, то |
||
|
An |
= c1 An−1 + c2 An−2 +... + ck An−k |
|
28

Bn = c1Bn−1 + c2 Bn−2 +... + ck Bn−k
Сложив эти соотношения, получаем
An + Bn = c1 (An−1 + Bn−1 )+ c2 (An−2 + Bn−2 )+... + ck (An−k + Bn−k ),
т.е.
Cn = c1Cn−1 + c2Cn−2 +... + ck Cn−k
□
Рекуррентные уравнения для нас важны, поскольку часто решение одной комбинаторной задачи удается свести к решению аналогичных задач меньшей размерности. Тем самым решение сложной задачи можно получить, последовательно находя решения более легких задач, и далее, пересчитывая по рекуррентным соотношениям, находить решение трудной задачи. Формула (4) является рекуррентным соотношением между элементами последовательности чисел an−k ,..., an . Т.о. рекуррентное соотношение
позволяет по известным значениям an−k ,..., an вычислить значение аn., но первые несколько значений a0 ,...,ak −1 нужно знать заранее. Как мы видели в
примерах, иногда удается получить из рекуррентного соотношения общую формулу для вычисления аn по номеру n. Тогда можно сразу вычислить окончательный результат без вычисления всех предыдущих результатов.
Пример. Вернемся к рекуррентному соотношению аn=аn-1+ аn-2. Оно задает так называемые числа Фибоначчи F0, F1, F2, F3, … , если положить F0 =0 и F1=1. Тогда последовательность решений будет иметь вид 0, 1, 1, 2, 3, 5, 8, 13, 21, …Найдем общую формулу для чисел Фибоначчи. Будем искать ее в виде
an = λn . Подстановка в рекуррентное соотношение дает λ n = λ n−1+ λn−2 . Разделим обе части равенства на λ n−2≠ 0 . Получим квадратное уравнение λ 2 − λ −1 = 0 . Найдем его корни
В соответствии с леммой 1 решением являются an =C1λ1n и an =C1λ2n , где C1
и C2 произвольные постоянные. В соответствии с леммой 2 решением будет их сумма. Т.о. общим решением будет линейная комбинация
Произвольные постоянные найдем из начальных условий a0=0, a1=1. Имеем a0 = 0 =C1 + C2 C2 = −C1
и
|
|
1 + 5 |
|
1 − 5 |
|
1 + 5 1 − 5 |
|
|
|
|||
a1 |
=1 =C1 |
|
|
+ C2 |
|
|
|
− |
|
|
=C1 |
5 |
|
|
|
|
|
||||||||
2 |
2 |
=C1 |
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|||||
29

Тогда C1 = 15 , C2 = − 15 . Окончательно общее решение рекуррентного соотношения будет иметь вид
который называется формулой Бине.
□
Заметим, что деление отрезка такое, что отношение длин полученных частей
равняется |
−1 + |
5 |
называют золотым сечением. |
Поэтому это число часто |
|||||
|
2 |
|
|
|
|
|
|
|
|
называют отношением золотого сечения. |
|
|
|
|
|||||
Рассмотренный пример позволяет сформулировать общий прием |
|||||||||
решения линейных рекуррентных уравнений. |
|
|
|
||||||
Теорема. |
Пусть |
an + c1an−1 +... + ck an−k |
= 0 |
– |
линейное |
однородное |
|||
рекуррентное уравнение |
с |
постоянными |
коэффициентами |
ci =Const |
|||||
(i =1,2,...k ), |
и |
пусть |
λ |
— корень |
характеристического |
уравнения |
|||
λk + c1λk −1 +... + ck = 0 . Тогда:
1) последовательность с общим членом C λ n , где С — произвольная
константа, удовлетворяет исходному однородному рекуррентному уравнению;
2) если λ1 ,λ2 ,...,λk — простые корни характеристического уравнения, то общее решение рекуррентного соотношения имеет вид
где Сi, i= 1,2, ..., k, — произвольные постоянные;
3) если λi — корень кратности ri, i =1, ..., s, характеристического уравнения, то общее решение рекуррентного соотношения имеет вид
где Ci j — произвольные постоянные. |
|
|
|
|
||
Пример. |
Рассмотрим |
соотношение |
an = 3 an−1 − 2 an−2 , |
a1 =1, a2 = 3. Оно |
||
является |
линейным |
рекуррентным |
|
соотношением |
с постоянными |
|
коэффициентами an |
−3 an−1 + 2 an−2 |
= 0 . |
|
Составим характеристическое |
||
уравнение |
λ2 −3 λ + 2 = 0 . Его корни λ |
|
=1,2 . Поэтому общее решение |
|||
|
|
|
1, 2 |
|
|
|
имеет вид an =C1 + C2 2n . С учетом начальных условий имеем
C1 + 2 C2 =1
C1 + 4 C2 =3
Тем самым C1 = -1, С2 = 1. Окончательное решение будет an = 2n −1.
30
