Классификация ошибок измерения

Любая физическая величина может быть измерена путем сравнения её с однородной величиной, принятой за единицу (эталоном).

Измерения бывают прямые и косвенные. В результате прямых измерений определяемая физическая величина получается сразу, непосредственно. Примерами прямых измерений служат определения длины (линейкой, штангенциркулем), силы электрического тока (амперметром). При косвенных измерениях искомая величина вычисляется по результатам прямых измерений других величин, связанных с искомой некоторой формулой.

Любое измерение не может быть абсолютно точным. Между истинным Х_ИСТ и измеренным значением физической величины Х существует некоторая разность

ΔХ = ½Х – Х_ИСТ½, (1.1)

которая называется абсолютной ошибкой результата измерения.

Чтобы охарактеризовать качество измерения и иметь возможность сравнить результаты измерений различных физических величин, вводится понятие относительной погрешности, под которым подразумевают отношение абсолютной ошибки измерения к истинному значению измеряемой величины.

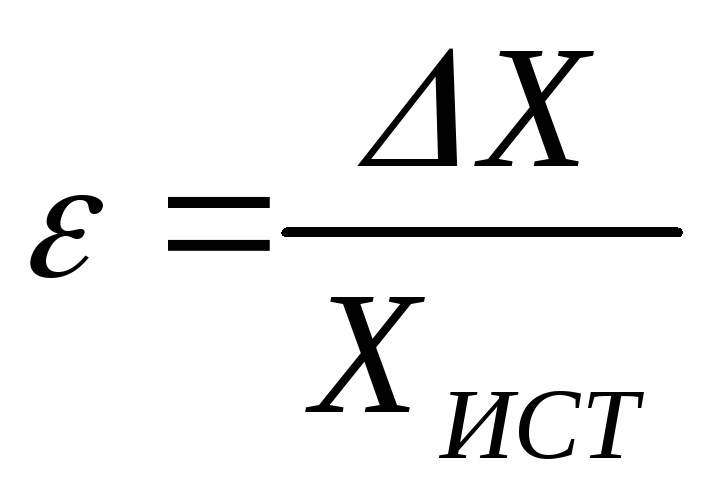. (1.2)

Чем меньше относительная погрешность, тем выше точность измерения. Погрешности, или ошибки измерения, можно разделить на три класса: грубые ошибки, или промахи; систематические ошибки; случайные ошибки.

Грубые ошибки появляются в результате небрежности, невнимательности экспериментатора (неправильные отсчеты по прибору, неправильная запись результата и т.п.). В большинстве случаев промахи хорошо заметны, так как резко отличаются от результатов других измерений.

Систематические ошибки могут быть вызваны методикой постановки эксперимента, ограниченной точностью измерительных приборов, дефектами самого объекта исследования и т.д. Величина и знак систематической погрешности могут оставаться неизменными при многократном повторении одних и тех же измерений. В некоторых случаях влияние систематических погрешностей на результат измерения можно учесть, если ввести соответствующие поправки.

Случайные ошибки обусловлены действием самых разнообразных и неконтролируемых причин. Поэтому результаты повторных измерений одной и той же физической величины могут не совпадать даже при том, что они проводятся в неизменных условиях одним и тем же методом (такие измерения называют равноточными).

Случайные ошибки могут иметь любую величину, положительный или отрицательный знак. Ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются в среднем одинаково часто. Закономерности, которым подчиняются случайные ошибки, и способы их оценки изучают в разделе математики «Теория ошибок», основанном на законах теории вероятности и математической статистики.

Методика расчета случайных ошибок прямых измерений

Пусть измеряется n раз некоторая физическая величина Х. Из-за случайных погрешностей, возникающих в процессе измерения, мы получаем набор значений Х₁, Х₂, Х₃, ..., Х_n. Наиболее близким к истинному значению Х_ИСТ будет среднее арифметическое

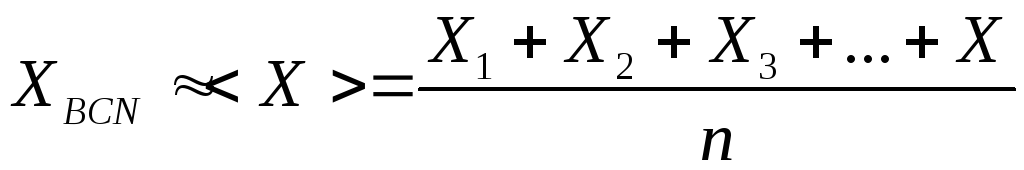. (1.3)

Чем больше измерений, тем ближе < X > и Х_ИСТ, а при

.

В реальном эксперименте число измерений всегда ограничено, поэтому истинное значение измеряемой величины остается неизвестным. Результаты отдельных измерений Х_i и среднее арифметическое < X > всегда содержат ошибку, поэтому вместе с результатом измерений нужно указать возможную величину ошибки, т.е. представить результат в виде

_.

Эта запись равнозначна неравенству

. (1.4)

Существует несколько способов оценки случайной ошибки DХ. Мы рассмотрим один из них, наиболее часто используемый при обработке результатов эксперимента. По результатам измерений рассчитывают так называемую среднюю квадратическую ошибку среднего арифметического:

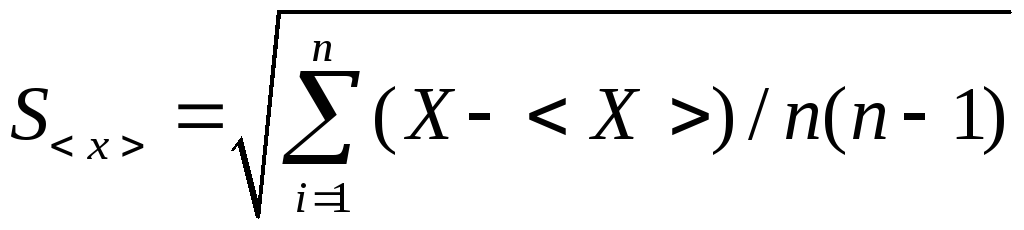. (1.5)

Так как результаты отдельных измерений Х_i и среднее арифметическое – случайные величины, то и S_{< Х >} тоже случайная величина. Поэтому мы не можем утверждать, например, что возможная ошибка DХ не превышает величины S_{< Х >}. Следовательно, нужно не только рассчитать возможную величину ошибки, но и указать вероятность того, что среднее арифметическое отличается от Х_ИСТ не более чем на величину DХ, т.е. вероятность, с которой выполняется неравенство (1.4).

Область значений называется доверительным интервалом, а соответствующая вероятность – доверительнойα. Доверительная вероятность является весьма важной характеристикой измерений, так как позволяет судить о надежности полученного результата.

Для нахождения доверительной вероятности необходимо знать закон распределения случайной величины (Х_i; < Х >; S_{< Х >}). Наиболее часто встречается на практике распределение Гаусса (нормальное распределение):

_.

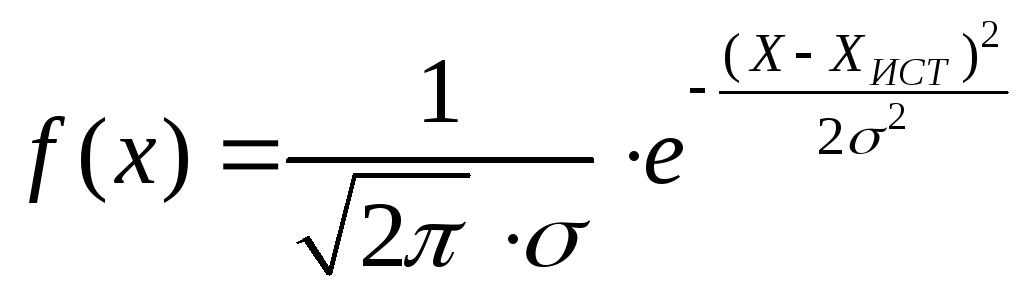Здесь f(х) – функция распределения случайной величины Х. Произведение f(х) · dх равно вероятности того, что случайная величина примет значение, заключенное между Х и Х + DХ.

Графически закон Гаусса представлен на рис. 1.5.

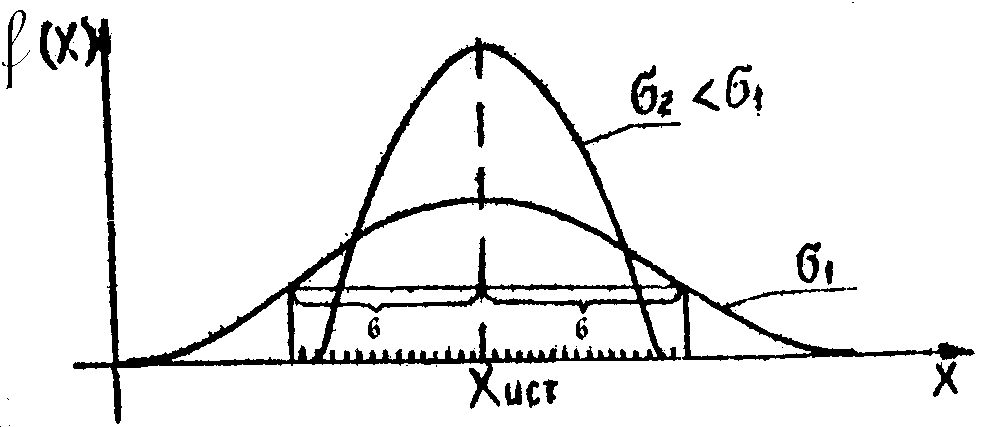
Рис. 1.5

Кривая Гаусса характеризуется двумя параметрами: Х_ИСТ и σ.

Х_ИСТ определяет положение вершины, а σ – ширину кривой (2 σ – расстояние между точками перегиба). Параметр σ называют стандартным отклонением или средним квадратическим. Он определяет разброс результатов измерений около Х_ИСТ, т.е. характеризует степень влияния случайных погрешностей на результаты измерений. На рис. 1.5 показаны две гауссовы кривые для разных значений стандартного отклонения (σ ₁ и σ ₂). В законе Гаусса σ ² носит название дисперсии случайной величины (дисперсия – разброс).

Среднее арифметическое, как случайная величина, тоже описывается законом Гаусса с параметрами ,

.

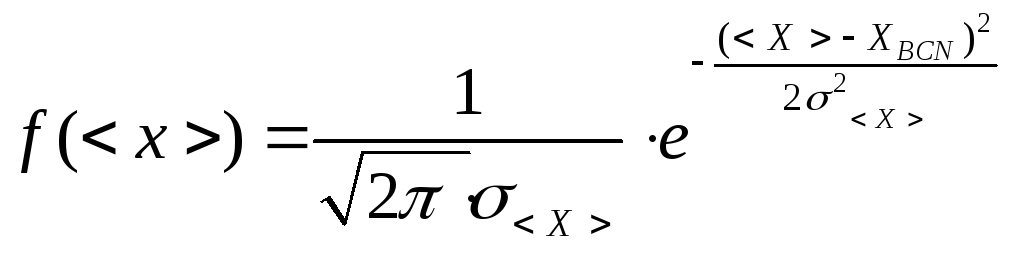Среднее значение является лучшей оценкой для Х_ИСТ, чем результат отдельного измерения, так как кривая f (< х >) в n раз уже.

При известном параметре σ _{< Х >} доверительная вероятность:

.

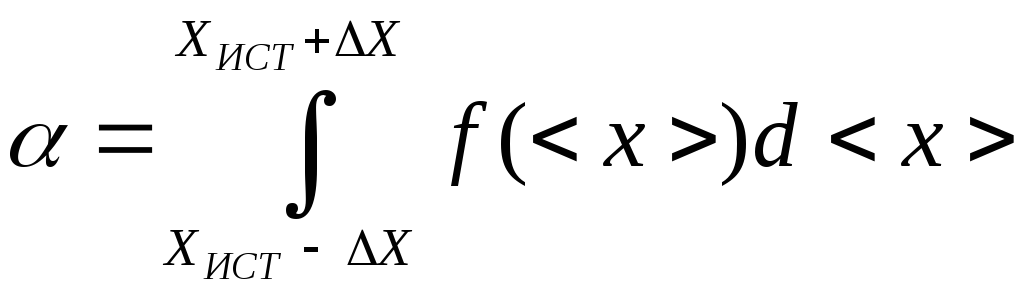Если задать доверительный интервал , то = 0,682; если , то, то.

Указанные значения доверительной вероятности относятся к бесконечно большому числу измерений. В практике физического эксперимента N часто не превышает 10, а параметр неизвестен. Если запринять, то доверительная вероятность, рассчитанная на основе закон Гаусса, оказывается завышенной.

Существует другой, более строгий метод определения доверительной вероятности, основанный на распределении Стьюдента, которое учитывает случайный характер величины . Распределение Стьюдента не содержит неизвестных параметровХ_ИСТ, и существенно отли­чается от гауссового при малом числе измерений (N < 30). В физическом лабораторном практикуме обычно ставится такая задача: по заданной доверительной вероятности нужно оценить величину доверительного интервала. На основе распределения Стьюдента доверительный интервал

,

где – коэффициент Стьюдента.

Существуют таблицы, в которых даны значения коэффициента Стьюдента для разных значений доверительной вероятности и различного числа измерений (табл. 1.1).

Таблица 1.1