Matematika_shpory

Квадратная матрица порядка n – таблица чисел, состоящая из n строк и n столбцов.

Определитель матрицы (детерминатор) – число, составленное из элементов матрицы по определенному правилу.

Минор элемента a_ik и определителя матрицы А – определитель, полученный из А путем вычеркивания i-ой строки и k-столбца (M_ik), т.е. определитель порядка n-1.

Алгебраическое дополнение элемента a_ik – соответствующий минор M_ik, умноженный на знаковый множитель.

A_ik = (-1)^i+k • M_ik

Свойства определителя:

• величина определителя не меняется при замене строк столбцами (операция транспонирования);

• перестановка местами двух любых строк (столбцов) меняет знак определителя;

• определитель с двумя одинаковыми строками (столбцами) равен нулю;

• общий множитель элементов одной строки (столбца) можно вынести за знак определителя;

• прибавление элементов одной строки, умноженных на произвольное число, к элементам другой строки определителя не меняет.

Теорема разложения определителя: всякий определитель можно представить как сумму элементов любой строки или столбца, умноженных на соответствующие алгебраические дополнения

А = ∑ a_ik • A_ik

Решение системы линейных уравнений – совокупность из n чисел x_ik, которые обращают ее в верные равенства.

Решить систему – выяснить совместна она или нет.

Совместная система – система алгебраических уравнений, имеющая хотя бы одно решение.

Теорема Кронекера-Капелли: система уравнений совместна тогда, когда ранг расширенной системы равен рангу основной системы.

Определенная система – совместная система, имеющая единственное решение.

Неопределенная система – совместная система, имеющая более одного решения.

Эквивалентные системы – системы, имеющее одно и тоже общее решение.

Ранг матрицы – число, характеризующее наибольший порядок миноров данной матрицы, отличных от нуля.

Теорема 1: Если ранг совместной системы линейных уравнений равен числу неизвестных этой системы, то система имеет единственное решение.

Теорема 2: Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Формулы Крамера – решение систем линейных уравнений в виде отношения двух определителей.

x_i = i / 

Метод Гаусса: путем элементарных преобразований представить расширенную матрицу системы уравнений в треугольной форме, когда все элементы ниже главной диагонали обращены в нуль.

Действия над матрицами:

• равенство матриц (две матрицы одного порядка равны между собой, если равны их соответствующие элементы);

• сложение матриц (суммой матриц одинаковой размерности называется матрица, где a_ik + b_ik);

• умножение на число (произведением матрицы на число  называется матрица, где  • a_ik);

• умножение матриц (производится по принципу «строка на столбец», причем АВ ≠ ВА);

• умножение матрицы на столбец (порождает новый столбец по правилу «строка на столбец»);

Единичная матрица – матрица, включающая 1 по главной диагонали и 0 в остальных местах.

Обратная матрица: матрица А^-1 будет обратной для матрицы А, если А^-1 • А = Е.

Теорема: для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е.

А ≡  ≠ 0.

Матричная запись:

• А • Х = В;

• Х = А^-1 • В

Вектор – направленный отрезок, т.е. отрезок прямой, характеризующийся длинной и направлением.

Коллинеарный вектор – вектор, расположенный на параллельных прямых. Чтобы вектор а был коллинеарен вектору в нужно число к, удовлетворяющее условию а = кв.

Компланарный вектор – вектор, расположенный в параллельных плоскостях.

Линейные действия над векторами:

• сложение векторов: (а + в) + с = а + (в + с);

• вычитание векторов: а – в = а + (-в);

• умножение вектора на число: а (вс) = (ав) с и а (в + с) = ав + ас.

Исследование линейной зависимости векторов:

• два коллинеарных вектора смещаются на одну прямую и всегда линейно зависимы, т.к. условие коллинеарности а = кв есть условие линейной зависимости а – кв = 0;

• два неколлинеарных вектора смещаются на одну плоскость и всегда линейно независимы (иначе они были бы коллинеарны);

• три компланарных вектора смещаются на одну плоскость и всегда линейно зависимы;

теорема: любой вектор m на плоскости можно представить в виде линейной комбинации двух неколлинеарных векторов а и в:

m = ха + ув

• три некомпланарных вектора в пространстве всегда линейно зависимы (иначе они были бы компланарными);

• любые четыре вектора в пространстве линейно зависимы.

теорема: любой вектор m в пространстве можно представить в виде линейной комбинации трех некомпланарных векторов а, в, с:

m = ха + ув + zc.

Базис на плоскости – два любые неколлинеарные вектора, взятые в определенном порядке.

Базис в пространстве – три любые некомпланарных вектора, взятые в определенном порядке.

Координаты вектора в базисе – коэффициенты разложения этого вектора по векторам базиса: m = {k₁, k₂, k₃}.

Прямоугольная система координат – совокупность точки О и ортонормированного базиса i, j, k. Орты i, j, k имеют единичную длину, взаимно перпендикулярны и определяют направление осей x, y, z.

Координаты точки М – проекции точки на оси координат (x, y, z).

Геометрический смысл координат вектора – это проекция вектора на оси координат.

Направляющие косинусы вектора а – косинусы углов между вектором и осями координат и равны отношению прилегающего катета к гипотенузе, т.е. отношению координат вектора к его модулю.

Проекция точки А на ось – основание перпендикуляра АА’, опущенного из точки А на ось.

Свойства проекции:

• проекция а =  |a| Cos . Если угол  между а и осью острый, то знак «+», если тупой, то «-»;

• проекция суммы векторов на ось равна сумме проекций на ось;

• проекция k a = k проекция а, k – константа.

Линейные действия над векторами:

• сложение векторов означает сложение их координат;

• умножение вектора на число приводит к увеличению его координат на это число.

Скалярное произведение векторов а и в – число, равное произведению длин векторов на косинус угла между ними.

ав = |а| |в| Cos .

Свойства скалярного произведения:

• ав = ва (переместительный закон);

• а (в + с) = ав + ас (распределительный закон);

• если а || в, то ав = ав (т.к. Cos 0 = 1);

• если а  в, то ав = 0 (т.к. Cos 90 = 0);

Координатное представление скалярного представления:

вектора а = {а_x а_y а_z} и в = {в_x в_y в_z} разложим по ортам, перемножим скалярно ав = (а_xi а_yj а_zk)(в_xi в_yj в_zk), получим

ав = а_xв_x + а_yв_y + а_zв_z

Угол между векторами: Cos  = ав / |а| |в|.

Условие а || в: (коллинеарность) а = kв или а_x/в_x = а_y/в_y = а_z/в_z.

Условие а  в: ав = 0 или а_xв_x + а_yв_y + а_zв_z = 0.

Векторное произведение векторов а и в – третий вектор, который:

• с  а, с  в;

• |с| = |а| |в| Sin ,  ≡ (а^в);

• векторы а, в, с образуют правую тройку, т.е. кратчайшее вращение от а к в идет против часовой стрелки при взгляде навстречу с. Обозначается с = а х в = [ав].

Свойства векторного произведения:

• а х в = -в х а (антипереместительный закон);

• к(а) х в = к(а х в) (сочетательный закон);

• а х (в + с) = а х в + а х с.

Координатное представление:

Смешанное произведение трех векторов – сочетание векторного и скалярного произведений (а х в)с.

Свойства смешанного произведения:

• (а х в)с = а(в х с);

• авс = - вас;

• авс = вса = сав.

Координатное представление:

Линейное пространство – множество L и его элементы вектора, если определены:

• операция сложения (вычитания) двух векторов такая, что х  L, х  L, х + у  L, где х, у – векторы;

• операция умножения вектора на число такая, что х  L, а  R, ах  L.

Свойства: для операций сложения, умножения векторов действуют все стандартные свойства.

Евклидово пространство – линейное пространство L, если в этом пространстве определена операция скалярного произведения двух векторов.

Основная идея аналитической геометрии: главный геометричес-кий объект описывается с помощью решения уравнений. Зная геометрические свойства линий можно найти ее уравнение. И обратно.

Система координат на плоскости – способ, позволяющий численно описать положение точек на плоскости.

Вывод уравнения окружности:

• обозначим через М (х, у) произвольную точку линии;

• запишем равенством общее свойство всех точек линии;

• входящие в это равенство отрезки выразим через текущие координаты (х, у) точки М и другие параметры задачи.

1. Фигура окружность.

2. Общее свойство |ОМ| = R.

3. (х²+ у²) = R.

4. х²+ у² = R².

Способы построения прямой линии:

• задать одну точку на плоскости;

у – у₀ = k(х – х₀)

• задать две точки на плоскости;

(х – х₁)/(х₂ – х₁) = (у – у₁)/(у₂ – у₁), х/а + у/в = 1

• задать одну точку М₀ (х₀, у₀) и направляющий вектор а;

(х – х₀)/а₁ = (у – у₀)/а₂ – каноническое уравнение

• задать одну точку М0 (х0, у0) и нормальный вектор n;

Ах + Ву + С = 0, где С = -(А_х0 + В_у0)

• задать одну точку и угол наклона к оси Х.

у = kх + b, где k = tg  = a₂/a₁

Расстояние от прямой Ах + Ву + С = 0 до начала координат:

р = |С| / А² + В²

Расстояние от произвольной точки М₀ (х₀, у₀) до прямой Ах + Ву + С = 0:

d = |А_х0 + В_у0 + С| / А² + В²

Уравнение окружности. Вывод:

• общее свойство точек окружности |СМ| = R;

• переход к координатной форме общего свойства

(х – а)² + (у – в)² = R, (х – а)² + (у – в)² = R².

Эллипс – фигура, образованная точками плоскости, для каждой из которых сумма расстояний от двух данных точек постоянна и больше расстояния между этими точками.

х²/а² + у²/в² = 1.

Координата фокуса с = а² – в²

Гипербола – фигура, образованная точками плоскости, для каждой из которых модуль разности расстояний до двух данных точек плоскости постоянен и меньше расстояния между этими точками. Данные точки – фокусы, а расстояния между ними – фокальное расстояние.

• общее свойство точек |F₁M| – |F₂M| = 2a;

• переход к координатам дает каноническое уравнение гиперболы

х²/а² – у²/в² = 1.

Парабола – фигура, образованная точками плоскости, для каждой из которой расстояние до данной точки равно расстоянию до данной прямой, не проходящей через данную точку. Данная точка – фокус, а прямая – директриса.

• уравнение директрисы х = - р/2;

• общее свойство точек |MF| = |MN|;

• переход к координатам (х – р/2)² + у2 = х + р/2, у² = 2рх.

Преобразование координат на плоскости.

Параллельный перенос системы координат. Имеем прямоуголь-ную систему координат ХУ с центром в точке О (0, 0). Через некоторую точку О* (а, в) проведем новые оси координат, параллельные Х и У, сохранив направление и масштаб. Координаты произвольной точки М (х, у) в новой системе координат Х*У* примут значения

х* = х – а или х = х* + а

у* = у – в у = у* + в

т.е. параллельный перенос системы координат приводит к линейным преобразованиям координат.

Поворот системы координат. Систему координат ХУ с ортами i, j повернем на угол относительно начала координат и введем новые орты i*, j*. Выразим старые орты через новые

i = cos  i* - sin  j*

j = sin  i* + cos  j*

Радиус-вектор произвольной точки М (х, у) разложим по ортам i, j и перейдем от них к ортам i*, j*.

ОМ = {х, у} = хi + уj = x (cos  i* - sin  j*) + y (sin  i* + cos  j*) = (x cos  + y sin a) i* + (-x sin  + y cos ) j* = {x*, y*}

В результате получаем формулу преобразования координат при повороте осей на угол :

х* = х cos  + y sin 

y* = -x sin  + y cos 

Полярные координаты.

Пусть на плоскости дана точка О – полюс и луч ОР – полярная ось. Тогда положение точки М на плоскости определяет полярный угол  = МОР и радиус-вектор r = ОМ. Если полярная ось совпадает с осями координат ХУ, то

х = r Cos , y = Sin 

и обратный переход

r = x² + y², tg  = y / x.

Если полюс совпадает с фокусом эллипса, гиперболы, параболы и луч ОР направлен по оси симметрии в сторону более удаленной вершины, то уравнения всех трех кривых будут одинаковы

r = p / (1 –  Cos ),

где  - эксцентриситет, p – параметр. Для эллипса и гиперболы

p = b² / a.

Множество – совокупность некоторого числа однотипных элементов. Множество обозначают заглавной буквой (А, В, С), а его элементы строчными буквами (a, b, c). Например, множество натуральных чисел N = {1, 2, 3, 4, …}.

Функция у = f(х) на множестве Х – правило соответствия между этими множествами, при котором для каждого х  Х существует единственный элемент у  У.

• Между множествами Х и У установлено соответствие (Х У), если для любого х  Х указаны соответствующие ему у  У.

• Соответствие между Х и У взаимно-однозначно, если для любого х Х существует единственный элемент у  У и наоборот.

• Два множества Х и У эквивалентны, если между ними можно установить взаимно-однозначное значение.

Общие свойства функций

Основные способы задания функций:

• табличный способ;

• аналитический способ (у = f(х), у = х²);

• графический способ.

Функция имеет явную форму у = f(х), если зависимая переменная стоит слева в первой степени и неявную форму, если х и у связаны более сложным образом. Пример: у = х², у² + х² = R².

Обратная функция х = f-1(у) получается из прямой функции у = f(х), если в качестве аргумента взять у.

Пример: у = х² – прямая, х = у – обратная.

Функция четная, если смена знака аргумента не меняет значение функции f(-х) = f(х) и нечетная, если смена знака аргумента меняет общий знак функции f(-х) = -f(х).

Функция периодическая, если при изменении аргумента на постоянную величину значение функции не меняется f(х + а) = f(х). Наименьшее значение а называется периодом.

Пример: Sin(x + 2) = Sin(x).

Основные элементарные функции:

• постоянная у = с, с = const;

• степенная у = хⁿ, n  R;

• показательная у = а^х, а > 0, a ≠ 1;

• логарифмическая у = log_ax, а > 0, a ≠ 1;

• тригонометрические у = Sin(x), y = Cos(x), y = tg(x), y = ctg(x);

• обратные тригонометрические y = arcSin x, y = arcCos x и др.

Числовая последовательность а_n – последовательность значений функции, определенных для целочисленных аргументов, т.е. а_n = f(n), где n = 1, 2, 3. Всякая функция f(x), определенная на интервале (1, ), порождает свою числовую последовательность.

Предел числовой последовательности а_n – число а, такое, что с ростом n разность между числом и членом последовательности становится меньше любого другого наперед заданного числа, тогда а = lim а_n.

Бесконечно малая последовательность – последовательность с нулевым пределом, а процесс прохождения по ее элементам называется предельным процессом.

Бесконечно малая величина – величина х, если она стремиться к нулю, делается меньше любого наперед заданного числа, но 0 так и не достигает. Процесс изменения б.м.в. называется предельным процессом.

Теорема: функция, обратная к бесконечно малой, является бесконечно большой и наоборот.

Леммы о бесконечно малых.

Лемма 1: алгебраическая сумма конечного числа бесконечно малых при х  а является бесконечно малой.

Лемма 2: произведение ограниченной в окрестности точки а функции на бесконечно малую при х  а является бесконечно малой.

Сравнение бесконечно малых.

Пусть при х  а а(х) и в(х) – бесконечно малые, тогда:

• если lim (в/а) = 0, то в – бесконечно малая высш. порядка, чем а.

• если lim (в/аⁿ) ≠ 0, то в – бесконечно малая n-порядка, чем а.

• если lim (в/а) = 1, то а и в – эквивалентные бесконечно малые.

Теоремы о пределах:

• lim с = с, если с – const, предел постоянной величины равен этой величине;

• lim (х + у – z) = lim x + lim y – lim z, предел алгебраической суммы нескольких слагаемых равен алгебраической сумме пределов каждого из них;

• lim ху = lim х lim у, предел произведения нескольких сомножи-телей равен произведению пределов каждого из них;

• lim х/у = lim х / lim у, предел дроби равен пределу числителя, деленному на предел знаменателя, если знаменатель не равен 0;

• lim сf(x) = c lim f(х), если с – const, постоянную величину можно вынести за знак предела;

• lim хⁿ = (lim x)ⁿ:

• lim ⁿx = ⁿlim x.

Первый замечательный предел:

lim Sinx / x = 1, при х 0

Имеем окружность R = 1 и касательные AD, BD. Из прямоугольных ОАС и ОАD следует: Sin x = AC/1, tg x = AD/1. Точки А и В соединяют три линии: прямая АВ = 2АС = 2 Sin x, дуга АВ = 2х и ломанная ФВИ = 2АD = 2tgx. Из соотношения длин этих линий следует: 2Sinx < 2x < 2tgx. Значит, 1 < x/Sinx < 1/Cosx, 1 > Sinx/x > Cosx. При переходе в неравенстве к пределу х0 имеем lim Cosx =1, 1  lim Sinx/x  1, следовательно, lim Sinx/x = 1.

Натуральное число – основание логарифма, приводящее к высшей степени симметрии графиков показательной и логарифмической функций. Обозначается е = 2,72…

Средняя скорость – отношение пройденного телом пути к затраченному времени.

V_ср = [S(t) – S(t₀)] / (t – t₀)

Мгновенная скорость – средняя скорость, взятая за бесконечно малый промежуток времени.

V_мг = lim [S(t) – S(t₀)] / (t – t₀), при t  t₀

Производная функции f(x) - предел lim [f(x) – f(x₀)] / (x – x₀) = f(x₀)

Производная – предел отношения приращения функции к приращению аргумента.

Алгебраический смысл: производная в точке х показывает, во сколько раз быстрее изменяется функция, чем аргумент в окрестностях этой точки, т.е. дает сравнение двух «точечных» параметров.

Физический смысл: скорость. Продифференцировать уравнение движения S = S(t) – значит определить мгновенную скорость тела в каждый момент времени t.

Геометрический смысл: тангенс угла наклона касательной.

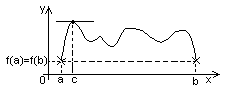
Теорема Роля: если функция f(x) непрерывна на заданном промежутке [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует точка с из интервала (a,b), такая, что f’(c)=0.

Теорема Коши: если f(x), g(x) удовлетворяет трем условиям:

• f(x), g(x) непрерывна на промежутке [a,b];

• f(x), g(x) дифференцируема на интервале (a,b);

• g’(x)0 на интервале (a,b), то существует точка с

g(b)  g(a) (неравны по теореме Ролля).

1. f(x) – непрерывна на [a,b]

2. f(x) – дифференцирована на (a,b);

3. f(a) = 0 ; f(b) = 0.

по теореме Ролля существует с  (a,b); f’(с) = 0.

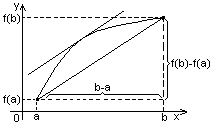
Теорема Лагранжа: если функция f(x) непрерывна на [a,b] и дифференцирована на (a,b), то существует точка с (a, b), такая, что: f(b) - f(a) = f’(c)(b - a).

Доказательство: применим теорему Коши, взяв только g(x)=x, тогда g’(x)=10.

Теорема Лопиталя: если функция f(x), g(x) дифференцирована в окрестности точки а, причем f(a) = g(a) = 0 и существует предел

Доказательство:

Достаточный признак экстремума функции: если f’(x)>0 на интервале (x0-б,х0) и f’(x)<0 на интервале (х0,x0+б) т.е. меняет знак с плюса на минус при переходе на точку х0, т.е. х0 – точка максимума f(x), а если же меняет знак с минуса на плюс, то х0 – точка минимума.

Доказательство:

Непрерывность функции.

Пусть задана функция z=f(x,y), р (х, у) - текущая точка, р₀(х₀,у₀) - рассматриваемая точка.

Функция z = f(x,y) называется непрерывной в точке р₀, если выполняются 3 условия:

• функция определена в этой точке f(р0) = f(x,y);

• функция имеет предел в этой точке lim f(р) = , p  p0

• предел равен значению функции в этой точке:  = f(x₀,y₀);

lim f(x,y) = f(x₀,y₀), p  p₀

Свойства:

• Если хотя бы 1 из условий непрерывности нарушается, то точка р называется точкой разрыва. Для функций 2х переменных могут существовать отд. точки разрыва и целые линии разрыва.

• Понятие предела и непрерывности для функций большего числа переменных определяется аналогично.

• Функцию трех переменных невозможно изобразить графически, в отличие от функции 2х переменных.

• Для функции 3-х переменных могут существовать точки разрыва, линии и поверхности разрыва.