1.10. Тесты рубежного контроля

1. Какой вывод о строении атома следует из опытов по рассеянию альфа-частиц?

(1) Положительные и отрицательные заряды одинаково распределены

(2) Положительный заряд сконцентрирован в маленьком тяжелом ядре

(3) Отрицательный заряд заполняет пространство вокруг ядра

(4) Электроны занимают произвольные уровни энергии

2. Частота фотона, поглощаемого атомом при переходе из основного состояния с энергией Е₀ в первое возбужденное с энергией Е₁ равна

(1) (Е₀ - Е₁)/h

(2) (Е₁ – Е₀)/h

(3) h/(Е₁ – Е₀)

(4) h/(Е₀ - Е₁)

3. Какое утверждение об опыте Франка-Герца – правильное

(1) был измерен удельный заряд электрона

(2) было открыто квантование энергии фотона

(3) было доказано, что энергия атомных состоянии квантована

(4) было доказано, что электрон имеет спин

4. В спектре атома водорода отношение длин волн головной линии серии Лаймана к длине волны головной линии серии Бальмера равно

(1) 27/5, (2) 1/2 (3) 1/4 (4) 5/27

5. Электрон разогнали в электрическом поле, разностью потенциалов 30 В. Длина волна де Бройля этого электрона равна

(1) 3,36·10 ^-10 м ( 2) 2,24·10 ^-10 м ( 3) 1,12·10 ^-10 м (4) 0,22·10 ^-10 м.

6. На рисунке представлена диаграмма энергетических уровней атома. Какой из отмеченных стрелками переходов между энергетическими уровнями сопровождается поглощением кванта максимальной длины волны?

(1). С уровня Е₁ на уровень Е₂ (2). С уровня Е₁ на уровень Е₅ (3). С уровня Е₇ на уровень Е₂ (4). С уровня Е₂ на уровень Е₁ .

7. Минимальная кинетическая энергия электрона локализованного в области атома (l ≈ 10^–10 м) по оценке через соотношение неопределенностей Гейзенберга равна

(1). 0,4 кэВ (2). 60 эВ (3). 4 эВ (4). 0,4 эВ.

1.10. Принципы оценивания

При правильном ответе на 7 вопросов теста оценка – «5»;

при правильном ответе на 5 или 6 вопросов теста оценка – «4»;

при правильном ответе на 3 или 4 вопроса теста оценка – «3»;

при правильном ответе на 2 и менее вопросов теста оценка-«2».

Модуль 2. Основы квантовой механики Комплексная цель модуля

В этом модуле рассмотрено уравнение Шредингера с центрально симметричным потенциалом. Волновая функция и ее свойства. Момент количества движения в квантовой механике. Квантовые числа. Уровни энергии.

2.1 Уравнение Шредигера

Э. Шредингер задался целью найти уравнение одним из решений которого являлась волна де-Бройля. В конце 1925 года Шредингеру удалось найти это уравнение. Это — основное уравнение нерелятивистской квантовой теории, уравнение Шредингера. Данное уравнение было именно найдено, оно является новым фундаментальным законом, который невозможно вывести из прежних представлений и теорий. Справедливость этого уравнения установлена тем, что все вытекающие из него следствия подтверждены экспериментом.

Сформулировав это уравнение, Шредингер сразу же применил его к атому водорода и получил для уровней энергии спектр, точно совпадающий со спектром по первоначальной теории Бора и соответственно — с результатами наблюдений.

Уравнение Шредингера играет в квантовой теории такую же роль, как основное уравнение динамики (2-й закон Ньютона) в нерелятивистской механике.

Особую роль в квантовой теории играют стационарные состояния — состояния, в которых все наблюдаемые физические величины не меняются с течением времени. Уравнение Шредингера для этого случая имеет следующий вид

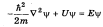(2.1)

Для микрочастиц из-за соотношения неопределенностей классическое определение состояния частицы (координаты и импульс), вообще говоря, утрачивает смысл. В соответствии с корпускулярно-волновым дуализмом в квантовой теории состояние части­цы задается пси-функцией Ψ(r,t), которая является комплексной величиной и формально обладает волновыми свойствами.

Понимание физического смысла пси-функции пришло после того, как выяснилось, что волновые свойства характерны для отдельных частиц. Этот факт можно истолковать по идее Борна (1926) так. Движение любой микрочастицы по отдельности под­чиняется вероятностным законам. Распределение вероятности, характеризующее это движение, проявляется в результате регистрации достаточно большого числа частиц. Это распределение оказывается таким же, как распределение интенсивности

волны: там, где интенсивность волны больше, регистрируется и большее число частиц.

В квантовой теории постановка вопроса состоит не в точном предсказании событий, а в определении вероятностей этих со­бытий. По значениям вероятностей согласно определенным правилам (см. ниже) можно найти средние случайных значе­ний физических величин, которые и доступны эксперименту. Пси-функция Ψ(г,t) и является той величиной, которая позволяет находить все вероятности.

Например, вероятность нахождения частицы в интересующем нас объеме dV^ в момент t определяется как

(2.2)

где Ψ* — комплексно-сопряженная функция. Отсюда плотность вероятности, т. е. вероятность нахождения частицы в единице объема,

Р = │Ψ│² dV = ΨΨ* dV (2.3)

Эта величина является экспериментально наблюдаемой, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению. Напомним, что в классике величины, характе­ризующие состояние частицы, являются принципиально наблюдаемыми.

Пси-функция, вообще говоря, определяется с точностью до произвольного постоянного множителя. Это не влияет на состояние частицы, которое она описывает. И тем не менее пси-функцию выбирают так, чтобы она удовлетворяла условию нормировки*:

(2.4)

где интеграл берется по всему пространству или по той области, в которой Ψ отлична от нуля. Условие нормировки (2.4) означает, что во всей области, где Ψ ≠ 0, частица находится с достоверностью. Пси-функцию, удовлетворяющую условию (2.4), называют нормированной.

Принцип суперпозиции. Итак, непосредственный физиче­ский смысл имеет не сама ^-функция, а квадрат ее модуля |*F|² или ¥¥*. И тем не менее в квантовой теории оперируют с ^-функцией, а не с экспериментально наблюдаемой величиной \¥\². Это необходимо для истолкования волновых свойств микрочастиц — интерференции и дифракции. Ситуация здесь со­вершенно идентична той, какую мы имеем в волновой теории. В волновой теории принимается принцип суперпозиции самих волновых полей, а не их интенсивностей. Именно так вводятся в теорию явления интерференции и дифракции.

Подобным же образом в квантовой теории принимается как один из основных постулатов принцип суперпозиции пси-функ­ций. Если у некоторой системы возможными являются состоя­ния 4*1 и ^Р₂> то для нее существует также состояние

Ψ = с₁ Ψ₁ + с₂ Ψ₂ (2.5)

где с₁ и с₂ – некоторые постоянные коэффициенты. Найдя, таким образом Ψ, можно далее определить и плотность вероятности ΨΨ* пребывания системы в этом состоянии.

Подтверждением принципа суперпозиции (2.5) является согласие с опытом вытекающих из него следствий.

В дальнейшем мы будем иметь дело только с уравнением (4.8) и будем записывать его (как это обычно принято) в виде

(2.6)

Еще раз напомним, что потенциальная энергия – функция U(r) – здесь определяется классически, как если бы никакими волновыми свойствами частица не обладала.

Квантование. В отличие от первоначальной теории Бора, где квантование вводилось искусственно, в теории Шредингера оно возникает автоматически. Достаточно только учесть, что физический смысл имеют лишь те решения уравнения (2.6), которые удовлетворяют естественным пли стандартным условиям. Эти условия состоят в том, что пси-функция ц/(г) должна быть конечной, однозначной, непрерывной и гладкой (т. е. без изломов) во всем пространстве, даже в тех точках (линиях, поверхностях), где потенциальная энергии U(г) терпит разрыв. Эти условия не представляют чего-нибудь особенного. Это обычные требования, накладываемые на искомое решение дифференциального уравнения.

Решения, удовлетворяющие этим условиям, оказываются возможными лишь при некоторых значениях энергии Е. Их назы­вают собственными значениями, а функции Ψ(r), являющиеся решениями уравнения (2.6) при этих значениях энергии, — собственными функциями, принадлежащими собственным зна­чениям Е. В этом и состоит естественный и общий принцип квантования.

Собственные значения энергии Е и принимаются за возмож­ные значения энергии в соответствующих стационарных состояниях. Эти значения энергии Е могут быть дискретными (квантованными) или непрерывными, образуя дискретный или непрерывный энергетический спектр.

В общем случае зависимости потенциальной энергии U(г) от координат, решение уравнения Шредингера представляет собой весьма громоздкую задачу. Но если все же нашли эторешение Ψ(r), то в принципе мы можем найти не только распределение вероятности местонахождения частицы, но также вероятности собственных значений различных физических величин (например, энергии, импульса, момента импульса). Надо только знать способ, как извлечь значения этих величин из функции Ψ(r). Но об этом в дальнейшем.

Заметим, что при более строгом рассмотрении стационарных состояний выясняется, что они вовсе не стационарные. Вместе с тем, решения уравнения Шредингера приводят к наличию строго стационарных состояний, в противоречии с известными экспериментальными фактами. Здесь проявляется очевидная ограниченность уравнений Шредингера: они не описывают радиационных переходов. Тем не менее, предсказываемые урав­нением Шредингера стационарные состояния с хорошей точностью соответствуют почти стационарным состояниям. Об этом свидетельствует опыт.

Теперь перейдем к рассмотрению нескольких простейших случаев, на которых проиллюстрируем, что квантование — это, действительно, естественное следствие вышеприведенных условий, накладываемых на решения уравнения Шредингера. При этом никаких дополнительных предположений делать не требуется.