Принцип Гюйгенса-Френеля

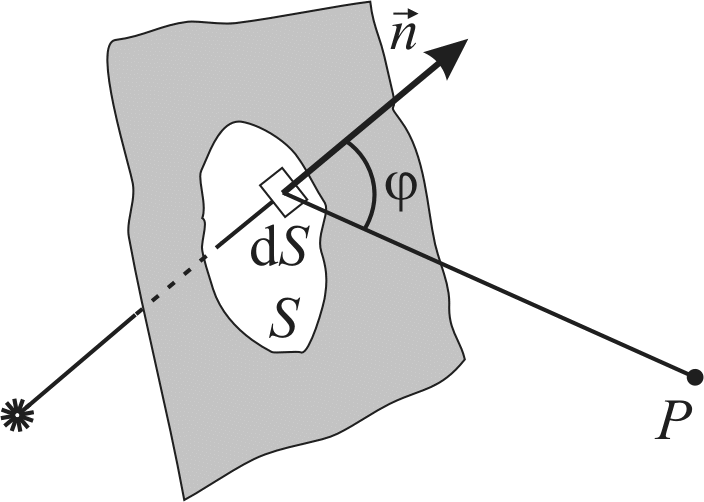
Рис. 6.1 Отверстие, вырезающее часть сферической волновой поверхности.

Рассмотрим преграду с отверстием произвольной формы, через которое проходит свет от точечного монохроматического источника (рис. 6.1). Отверстие вырезает некоторую часть сферической волновой поверхности площадьюS. По предположению Френеля каждый из элементарных участковэтой поверхности становится источником вторичной сферической волны. Амплитуда вторичной световой волны, достигающей т.P, пропорциональна амплитуде первичной волны, приходящей к элементуdS, площади самого элементаdS, и обратно пропорциональна расстояниюrот элементаdSдо т.P. Тогда от каждого элементаdSволновой поверхности распространяющаяся сферическая волна вызывает в т.Рколебание

, (6.1)

где a₀– величина, определяемая амплитудой световой волны в месте нахождения элементаdS,k– модуль волнового вектора, то есть волновое число (). Коэффициент К зависит от угламежду нормальюк элементуdSи радиус-вектором.

Результирующее колебание в т. Рможет быть представлено как суперпозиция колебанийdEот всех элементовdSповерхностиS:

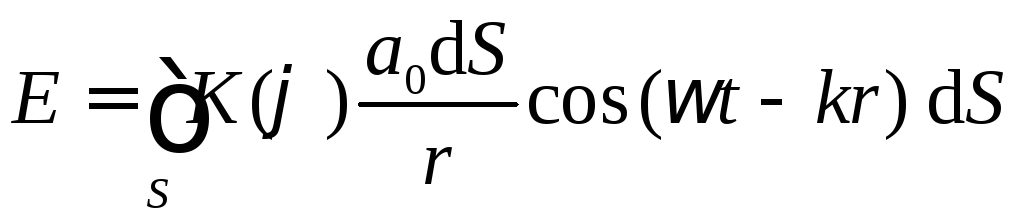. (6.2)

Рис. 6.2 Векторная диаграмма.

Интеграл (6.2) выражает собой математическую формулировку принципа Гюйгенса-Френеля: для определения колебания в т.Р, лежащей перед некоторой поверхностьюSнадо найти колебания, приходящие в эту точку от всех элементовdSповерхностиSи затем сложить их с учетом амплитуд и фаз. При этом предполагается, что колебания, испускаемые различными элементамиdS, являются когерентными.

Принцип Гюйгенса-Френеля можно представить с помощью векторной диаграммы (рис. 6.2). На диаграмме результирующая амплитуда (вектор) представлена как векторная сумма амплитудколебаний в т.Рот различных эле­ментов dSповерхностиSс учетом их фаз, т. е. углов между ними.

Метод Зон Френеля. Дифракция на круглом отверстии

В некоторых случаях интегрирование (6.2) может быть заменено простым алгебраическим или графическим сложением по методу зон Френеля. Для этого вырезанную отверстием волновую поверхность Sразбивают на зоны, конфигурация которых зависит от симметрии рассматриваемой задачи.

Рис. 6.3 Дифракция Френеля на круглом отверстии.

Определим амплитуду световых колебаний в т.Рза круглым отверстием на его оси (рис.6.3). Волновая поверхностьS, вырезанная отверстием, симметрична относительно прямойР₀Р, поэтому ее разбиваем на кольцевые зоны с центром на оси отверстия. Зоны выбираем так, чтобы расстояния от краев каждой зоны до т.Ротличались друг от друга на половину длины волны, для того что бы фазы приходящих от соседних зон колебаний отличались на.

Найдем внешний радиус -ой зоны Френеля. Из рис.6.3 видно, что

(6.3)

(6.4)

(6.5)

Раскрывая скобки и пренебрегая малыми членами ,,, выражения (6.4), (6.5) принимают следующий вид

.

С учётом выражения (6.3) получаем, что внешний радиус m-ой зоны Френеля определяется формулой

. (6.6)

Если падающая нормально на данное отверстие волна плоская (), то (6.6) примет вид

. (6.7)

Площади зон (при достаточно малых m) почти одинаковы

, (6.8)

но амплитуды колебаний, приходящих в т. Pот этих зон монотонно убывают из-за увеличения расстоянияr от каждой следующей зоны до т.Pи роста угламежду нормалью к элементам зоны и направлением на т.P.

Так как фазы колебаний, возбуждаемых в т. Рсоседними зонами Френеля, отличаются на, векторы-амплитуды соседних зон противоположны по направлению, а результирующая амплитуда от всех зон зависит от того чётное или нечётное число зон открыто отверстием. Если число зон нечетное, в т.Рнаблюдается максимум, если же число зон четное, то – минимум.

Рис. 6.4 Спираль Френеля.

Для расчёта амплитуды в т.Pиспользуем графический метод сложения амплитуд. Для этого мысленно разобьём волновой фронт на элементарные кольцевые зоны (гораздо более узкие, чем зоны Френеля). Колебание каждой последующей зоны отстаёт по фазе и чуть меньше по амплитуде от колебания, исходящего от предыдущей зоны, поэтому векторная диаграмма будет иметь вид цепочки, закрученной в спираль – спираль Френеля (рис. 6.4). Пусть– вектор амплитуды результирующего колебания в т.P. Начало этого вектора лежит в точке 0. В зависимости от числа открытых отверстием элементарных зон, конец этого вектора может лежать в любой точке спирали. Если конец вектора лежит в точке 0.5, то открыта половина первой зоны Френеля (), если в точке 1, то открыта только первая зона Френеля (), если в т. 2, то открыты только две первые зоны () и т.д. Если конец вектора лежит в т.F(фокус спирали), тобудет вектором амплитуды колебания, приходящего от всех зон (всей волновой поверхности).

Как видно из рисунка, амплитуда колебаний и интенсивность света в т. Pпо мере увеличения радиусаизменяется не монотонно. Пока открывается первая зона Френеля, амплитуда в т.Рувеличивается и достигает максимума при полностью открытой первой зоне (). Но по мере открывания второй зоны Френеля амплитуда колебаний в т.Рубывает, и при полностью открытых двух первых зонах уменьшается почти до нуля (). Затем амплитуда увеличивается снова и т. д. То же самое будет наблюдаться, если вместо увеличения отверстия приближать к нему т.Р.

Из векторной диаграммы видно, что , т. е. в отсутствие преграды интенсивность света в т.Pв четыре раза меньше, чем при наличии преграды с круглым отверстием, открывающем только первую зону Френеля. При отверстии, открывающем для т.Рдве зоны Френеля, интенсивность в этой точке падает практически до нуля, хотя световой поток через отверстие оказывается вдвое больше.