
- •Основы измерений и обработки результатов
- •1. Однократные измерения размера линейкой.
- •Ускорение свободного падения
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений.
- •Обработка результатов эксперимента
- •Баллистический маятник
- •Математический маятник
- •Упругий удар Цель работы: исследование удара, изучение законов сохранения импульса и механической энергии при ударе.
- •Коэффициент поверхностного натяжения
- •Измерение газовой постоянной
- •Теплоемкость жидкости
- •Колебания струны
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Вязкость жидкости
Лабораторная работа 1
Основы измерений и обработки результатов
Цель работы:знакомство с элементами теории погрешностей, методами измерения основных физических величин и правилами обработки результатов измерений.
Основные теоретические положения
(элементарные представления теории погрешностей)
Измерением называется процедура определения действительного значения физической величины с помощью специальных технических средств. Указанная процедура состоит из нескольких этапов: выбора измеряемой величины, метода измерения, приборов для наблюдения, метода обработки результатов наблюдения. Поэтому результаты наблюдения, как правило, не дают истинного значения измеряемой величины, то есть они содержат погрешности измерений.
По способу получения результата все измерения делятся на прямые и косвенные. Измерение, при котором значение физической величины находится непосредственно из опытных данных, называется прямым измерением – это, например, измерение температуры термометром, длины – линейкой.
Измерение, при котором искомое значение физической величины вычисляют по формуле на основании известной зависимости между ней и величинами, получаемыми при прямых измерениях, называется косвенным измерением, − например, измерение плотности тела по его массе и геометрическим параметрам, сопротивление проводника по напряжению и току.
Погрешность измерения – это отклонение результата измерения от истинного значения, которое может быть получено с помощью более совершенных методов и средств измерений. Различают абсолютную и относительную погрешности.
Абсолютная погрешность ΔX равна разности между результатом измеренияXи истинным или точным значением измеряемой величины:
![]() .
(1.1)
.
(1.1)
Относительная погрешность измерения
![]() представляет собой отношение абсолютной
погрешности к истинному или точному
значению измеряемой величины:
представляет собой отношение абсолютной
погрешности к истинному или точному
значению измеряемой величины:
![]() (1.2)
(1.2)
Погрешности измерения имеют случайную и систематическую составляющие.
Составляющая погрешности измерения, которая случайным образом изменяется при повторных измерениях одной и той же величины, называется случайной погрешностью. Случайная погрешность определяется факторами, проявляющимися нерегулярно с изменяющейся интенсивностью. Значение случайной составляющей невозможно предвидеть, следовательно, исключить.
Случайная погрешность прямых измерений вычисляется следующим образом:
![]() .
(1.3)
.
(1.3)
Здесь![]() − коэффициент Стьюдента,
− коэффициент Стьюдента, ![]() − среднее квадратичное отклонение,
вычисляемое по формуле
− среднее квадратичное отклонение,
вычисляемое по формуле
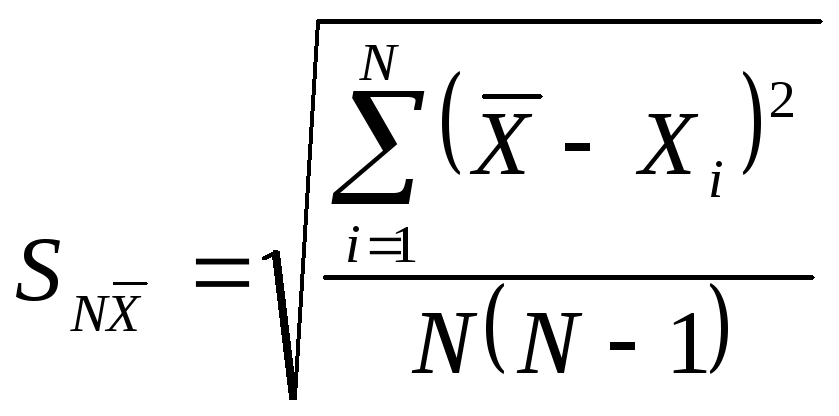 , (1.4)
, (1.4)
а ![]() − среднее значение измеряемой величины
− среднее значение измеряемой величины
![]()
![]() .
(1.5)
.
(1.5)
Результат измерения представляется в виде
![]() .
.
Для нахождения предельной случайной
абсолютной погрешности косвенных
измерений в том случае, когда интересующая
экспериментатора величина
![]() связана
с несколькими измеряемыми величинами
связана
с несколькими измеряемыми величинами![]()
![]() функциональной зависимостью
функциональной зависимостью
![]() (1.6)
(1.6)
используется формула
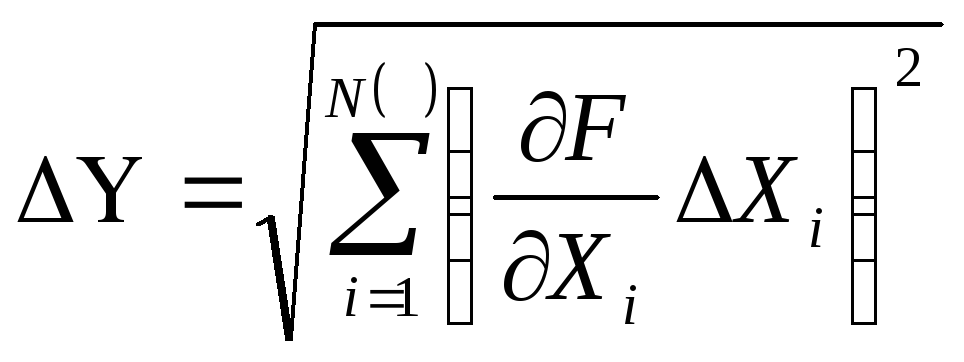 .
(1.7)
.
(1.7)
Предельная относительная погрешность рассчитывается по формуле:
 .
(1.8)
.
(1.8)
Результат измерения представляется в виде
![]() ,(1.9)
,(1.9)
где
![]()
Отдельные результаты измерений могут сильно отличаться от среднего значения, что вызывается кратковременным и сильным воздействием какого-либо внешнего фактора. Возникающая при этом погрешность называется промахом. Ошибочный результат наблюдения в этом случае должен быть исключен при обработке результатов измерения.
Погрешности, которые при повторных измерениях остаются постоянными или закономерно изменяются, называются систематическими. Их можно оценить или исключить из результатов измерений путем введения поправок.
Систематические погрешности классифицируются следующим образом:
1. Систематические погрешности, о существовании которых ничего не известно, но которые могут иметь значительную величину.
Такие погрешности проявляются при сложных измерениях и их почти никогда не удается устранить. Измерение с такой ошибкой является неверным.
2. Погрешности известного происхождения, но неизвестной величины, которые не могут быть исключены, но могут учитываться в конечном результате. Наиболее распространенной погрешностью такого типа является погрешность измерительных приборов, определяемая классом его точности.
3. Систематические погрешности, природа которых известна, а их величина может быть установлена более или менее точно. Для устранения таких погрешностей в измерения вводятся поправки.
Различают систематические погрешности прямых и косвенных измерений. Систематическая погрешность прямого измерения – это, как правило, величина погрешности при нормальных условиях эксплуатации средства измерения.
В случае применения нескольких средств измерений, образующих комбинированное устройство, возникает систематическая погрешность косвенных измерений, предельная величина которой рассчитывается по формуле, аналогичной (1.7):
 , (1.10)
, (1.10)
где функция ![]() ,
,![]() − систематическая погрешность каждого
отдельно взятого измерительного
средства, входящего в устройство.
− систематическая погрешность каждого
отдельно взятого измерительного
средства, входящего в устройство.
В большинстве случаев результаты эксперимента содержат и систематические, и случайные погрешности. Поэтому целесообразно организовать эксперимент таким образом, чтобы исключить одну из них. Для этого можно использовать следующие правила:
1. Если систематическая погрешность значительно больше случайной, то нет смысла уменьшать случайную погрешность, увеличивая число экспериментов, и достаточно осуществить наблюдение один раз.
2. Если случайная погрешность является определяющей, то для уменьшения число наблюдений следует выбирать таким, чтобы случайная погрешность среднего арифметического была меньше систематической погрешности. В этом случае результирующая погрешность определяется, в основном, систематической погрешностью.
3. Если в эксперименте присутствуют систематические погрешности неизвестного типа и большой величины, то их можно устранить, организовав измерение таким образом, чтобы постоянный фактор, вызывающий систематическую погрешность, в каждом из наблюдений действовал различным образом. В результате такой организации эксперимента постоянно действующий фактор становиться случайным, а систематическая погрешность превращается в случайную. Этот прием называется рандомизацией и позволяет практически исключить многие неизвестные погрешности.
Если все же не удается обеспечить исключение погрешности, какого–либо типа, то при обработке результатов эксперимента возникает необходимость суммирования погрешностей.
В простейшем случае величина предельной суммарной погрешности прямых измерений вычисляется по формуле
![]() , (1.11)
, (1.11)
где ![]() −
значение коэффициента Стьюдента при
−
значение коэффициента Стьюдента при
![]() .
.
Величина предельной суммарной погрешности косвенных измерений рассчитывается по формуле
![]() .(1.12)
.(1.12)
Все измерения осуществляются с помощью средств измерений – технических устройств, имеющих нормированные метрологические характеристики. Применяемые на практике средства измерений подразделяют на измерительные приборы, измерительные преобразователи, измерительные установки и измерительные системы.
Важнейшей характеристикой средств измерений является их точность, которая характеризуется соответствующими составляющими погрешности результата измерений.
Погрешность средств измерений – это метрологическая характеристика, количественно выражающая отклонение номинального значения физической величины, воспроизводимой или измеряемой данным средством измерений, от истинного или точного значения.
Различают абсолютную, относительную и приведенную погрешности измерительных приборов.
Абсолютная погрешность прибора
![]() есть
разность между показанием прибора А и
истинным значением измеряемой величины
есть
разность между показанием прибора А и
истинным значением измеряемой величины ,
то есть
,
то есть
![]() (1.13)
(1.13)
Относительная погрешность представляет
собой отношение абсолютной погрешности
![]() к истинному значению
к истинному значению![]() измеряемой величины:
измеряемой величины:
![]() .
(1.14)
.
(1.14)
Приведенная погрешность
![]() есть отношение абсолютной погрешности
есть отношение абсолютной погрешности![]() к
нормирующему значению
к
нормирующему значению![]() ,
то есть условно принятому значению
физической величины, постоянному во
всем диапазоне измерений или некоторой
его части:
,
то есть условно принятому значению
физической величины, постоянному во
всем диапазоне измерений или некоторой
его части:
![]() .
(1.15)
.
(1.15)
Важной эксплуатационной характеристикой
прибора является чувствительность S,
то есть отношение изменения сигнала на
выходе измерительного прибора![]() к вызывающему его изменению измеряемой
величины:
к вызывающему его изменению измеряемой
величины:
![]() .
(1.16)
.
(1.16)
Величина, обратная чувствительности
![]() ,
называется ценой деления прибора.
,
называется ценой деления прибора.
Более подробно указанные характеристики описаны для электроизмерительных приборов в лабораторной работе 11 настоящего руководства.
Описание лабораторной установки и последовательность проведения измерений
Установка представляет собой специальный ящик, в котором представлен набор измерительных инструментов: линейка, штангенциркуль, микрометр, транспортир, секундомер, термометр, а также исследуемые объекты: параллелепипед, неравноугольный треугольники сосуд с нагревателем.
Задание 1. Измерение линейных размеров с помощью линейки, штангенциркуля и микрометра.
