Колебания струны

Цель работы: изучение волновых явлений, условия существования стоячих волн, исследование упругих свойств струны.

Основные теоретические положения

Пусть точка, совершающая колебания, находится в среде, все частицы которой связаны между собой. Тогда энергия колебаний точки может передаваться окружающим точкам, вызывая их колебания. Явление распространения колебаний в среде называется волной. При этом колеблющиеся частицы не перемещаются с распространяющимся колебательным процессом, а колеблются около своих положений равновесия.

Если в неограниченной среде беспрепятственно распространяется единственная волна, то она называется бегущей. Составим уравнение бегущей волны, позволяющее определять смещение любой точки волны в любой момент времени.

Р

Рис. 9.1. К выводу уравнения бегущей волны

ассмотрим непрерывную однородную среду− струну, которая на концеx=0 присоединена к источнику гармонических колебаний в момент времени t’:D(t’)=Asint’. Найдём смещение элементов струны, как функцию координаты x и времени t, то есть функцию . Очевидно, что для точкиx=0, =D(t’)=Asint’ (рис. 9.1). Предположим, что бегущее по струне в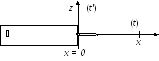озмущение распространяется с некоторой скоростью. Смещение элемента струныx в момент t равно смещению элемента x=0 в момент t’ =, если расстояние между ними равно расстоянию, которое возмущение проходит за время t-t’ со скоростью . Тогда точкиx=0 и x=x колеблются в одной фазе: x=(t-t’), ,. Поэтому уравнение бегущей синусоидальной волны == Asint’, то есть

. (9.1)

Преобразуем функцию (9.1): . Обозначим=k и назовём его волновым числом, тогда =. Следовательно, скорость,. Величину, равную расстоянию, которое возмущение преодолевает за период колебаний, назовём длиной волны, то есть, тогда,.

Уравнение (9.1) и есть уравнение бегущей одномерной (или плоской) волны. При заданном x оно позволяет определить положение точки (с координатой равновесного положения x) в любой момент времени t. При заданном t оно позволяет определить мгновенные положения всех колеблющихся точек.

Таким образом, видим, что в волновом движении имеет место двоякая периодичность. С одной стороны, каждая частица среды совершает периодическое движение во времени, с другой стороны, в каждый момент времени все частицы располагаются на линии, форма которой периодически повторяется в пространстве.

Определим скорость распространения продольных колебаний вдоль бес­конечно длинного стержня с постоянным поперечным сечением.

П

Рис. 9.2. Распространение упругой деформации вдоль стержня

ридействии на левое сечение силой (рис. 9.2) вблизи этого сечения происходит уплотне­ние материала стержня, и возникает деформация сжатия. Появляются упругие силы, стремящиеся восстановить первоначальную плотность, в результате чего возникает сжатие соседних областей и таким образом локальное возмущение плотности вблизи левого края стержня распространяется вправо со скоростью . Импульс силы упругости равен . Если Е − модуль сжа­тия, иначе называемый модулем Юнга, то. За время деформация распространяется на расстояние . Масса участкастержня, охваченная деформацией, увеличится на вследствие уве­личения плотности материала на.Так как ,то . В соответствии со вторым зaконом Ньютона импульс силы упругости равен изменению импульса, то есть . Подставляя все величины, получим

или , (9.2)

где - погодная плотность материала стержня.

Уравнение (9.1) описывает волну, распространяющуюся в положитель­ном направлении оси ох. При изменении направления распространения волны на противоположное второе слагаемое в аргументе косинуса изменяет знак, так как заменяется на

. (9.3)

Рассмотрим теперь распространение волны в струне, закрепленной с обеих сторон. При этом волна, движущаяся в одном направлении, достигнув второго закрепленного конца струны, отразится и станет распространяться в противоположном направлении. Таким образом вдоль длины струны возникнет явление наложения волн, распространяющихся в противоположных направлениях. Если свойства среды не изменяются под воздействием распространяющейся волны, то будет выполняться принцип суперпозиции, согласно которому каждая волна распространяется в среде независимо от других. В этом случае результирующее смещение z частиц среды будет определяться как сумма смещений z₁ и z₂, обусловленных прохождением отдельных волн. В результате будет наблюдаться в различных точках среды усиление или ослабление колебаний в зависимости от фаз приходящих возмущений.

Сложение волн, при котором в разных точках среды образуются усиления и ослабления амплитуды колебаний, называется интерференцией волн. Такая интерференционная картина сохраняется во времени.

Рассмотрим интерференцию двух волн с одинаковой амплитудой, распространяющихся в противоположных направлениях, как в случае струны, закрепленной с обеих сторон. При этом необходимо учитывать следующее явление. После отражения от закрепленного конца отраженная деформация имеет противоположный знак. Это становится понятным, если учесть, что так, как смещение закрепленного конца все время отсутствует, у точки крепления развиваются силы, препятствующие приходящему изгибу струны. Эти силы порождают изгиб противоположного знака, начинающий распространяться в обратную сторону. Поэтому и в отраженной деформации знак смещения изменяется на обратный. Если отражается гармоническая волна, то такое изменение равносильно «потере» полуволны при отражении.

Таким образом, наложение двух волн даст следующее:

.

Используя формулу разности синусов, получим

. (9.4)

Это выражение называется уравнением стоячей волны, при этом предполагается режим установившихся колебаний, то есть режим, возникающий после многократного пробега волн между креплениями струны. Из (9.4) видно, что в стоячей волне все точки среды (любое значение x) колеблются по гармоническому закону с круговой частотой .

Амплитуда колебаний различна для разных точек и определяется из (9.4) следующим образом:

. (9.5)

Из последнего выражения вытекает, что есть точки среды, называемые узлами, в которых колебания отсутствуют Z_m = 0, следовательно, z = 0. Координаты этих точек определятся из условия равенства нулю синуса в выражении (9.5), то есть

. (9.6)

Отсюда, так как , получаем

.

Следовательно, расстояние между соседними узлами равно половине длины волны. Так как узлы все время остаются в покое, то в стоячей волне нет направленного переноса энергии, энергия не может перейти через узел. Передача энергии по струне производится только бегущей волной.

Те точки, в которых значение амплитуды достигает максимума , называются пучностями. Как следует из выражения (9.5), координаты этих точек определяются из условия, то есть отвечают уравнению. Видим, что расстояние между соседними пучностями также равно половине длины волны.

Множитель при переходе через узел меняет знак, вследствие чего фаза колебаний по разные стороны от узла отличается на. Все точки, находящиеся между двумя соседними узлами, колеблются в одинаковой фазе (их отклонения имеют одинаковый знак). Условие неподвижности обоих концов закрепленной струны приводит к тому, что на длине струны должно укладываться целое число полуволн:

. (9.7)

Таким образом, стоячая волна образуется только при надлежащем соотношении размеров струны и длины волны (частоты колебаний). Для разных значений n = 1, 2,… получим различные типы, или моды, колебаний, при этом n определяет число пучностей, а не узлов. Из (9.6) с учетом (9.7) получим формулу для частот, при которых в струне устанавливаются стоячие волны

, (9.8)

Частоты называют собственными частотами струны. Частоту называют основной частотой, остальные – обертонами. Видим, что определяемые формулой (9.8) собственные частоты не зависят от модуля Юнга материала. Этот результат является следствием того, что мы пренебрегли изменением натяжения струны при колебаниях.

В общем случае в струне могут одновременно существовать колебания с различными собственными частотами. Так, наряду с основным тоном n = 1, могут возбуждаться обертоны n = 2, 3, 4,….

Полученные выше уравнения описывают движение идеально гибкой струны в вакууме. При колебаниях реальной струны всегда происходят потери энергии.

Часть энергии теряется вследствие трения о воздух, другая часть уходит через концы струны и т.д. Для поддержания незатухающих колебаний служит вибратор. Если энергия потерь в точности компенсируется энергией, поступающей от вибратора, то в струне можно наблюдать стоячие волны. Но теперь по струне должна происходить передача энергии. Поэтому наряду со стоячими будут существовать бегущие волны, в результате чего узлы окажутся несколько размытыми. Если потери энергии за период малы по сравнению с запасом колебательной энергии в струне, то искажение стоячих волн бегущей волной будет незначительным.

Другим приближением в изложенной выше теории является пренебрежение неоднородностью струны. В реальной струне и плотность, и натяжение могут являться непрерывными функциями координаты Х. Например, если струна подвешена вертикально, то учет массы струны приведет к тому, что натяжение в верхних частях будет больше, чем внизу. Любая неоднородность приведет к искажению формы колебаний, так как синусоидальные колебания в пространстве характерны только для нормальных мод однородных систем.