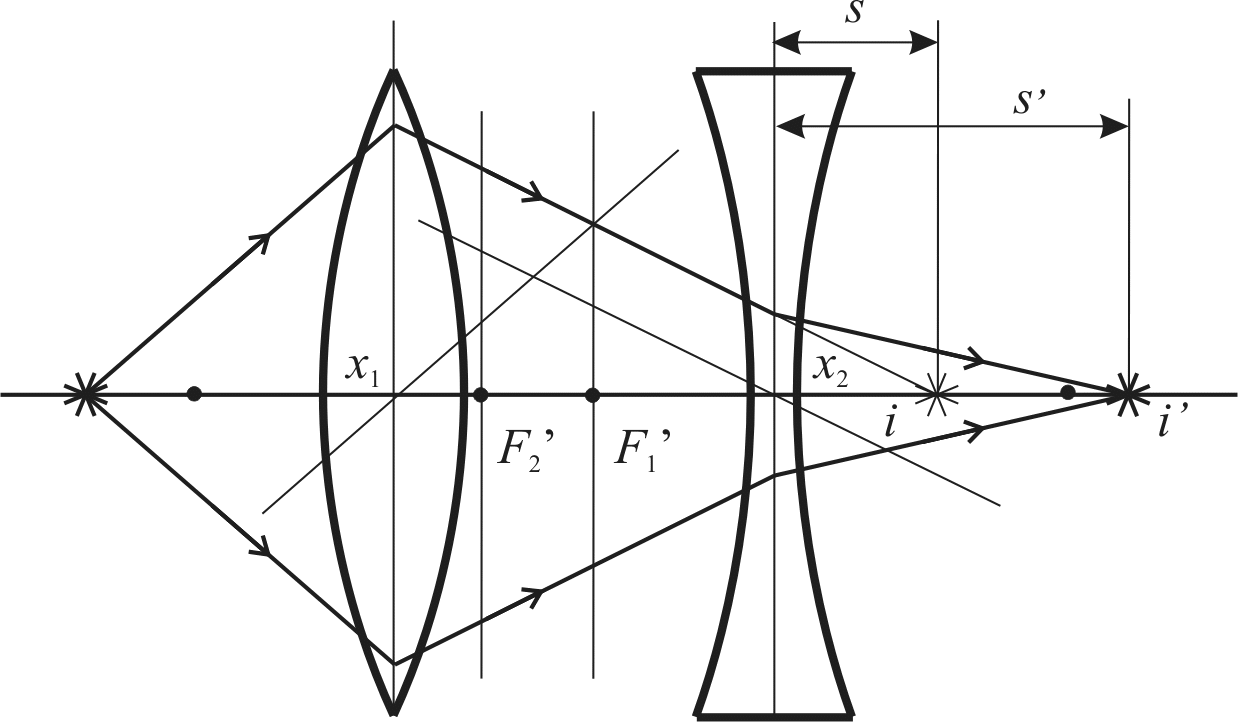Министерство образования и науки Российской Федерации

ГОУ ВПО Саратовский государственный технический университет

Оптика – 2 Методические указания по выполнению лабораторных работ по физике для студентов всех специальностей

Одобрено редакционно-издательским советом Саратовского государственного технического университета

Саратов 2006

Настоящие методические указания представляют описание четырех лабораторных работ нового физического практикума кафедры прикладной физики:

«определенииe фокусных расстояний собирающей и рассеивающей линз»,

«ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ДИФРАКЦИОННОЙ РЕШЁТКИ»,

«ИССЛЕДОВАНИЕ ЗАКОНА МАЛЮСА И ПРОХОЖДЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА ЧЕРЕЗ ФАЗОВУЮ ПЛАСТИНКУ»,

«ДИСПЕРСИЯ СВЕТА».

Каждое описание состоит из следующих разделов:

• цель работы,

• основные теоретические положения,

• экспериментальная установка и методика измерений,

• порядок выполнения работы и обработка результатов эксперимента.

Для расчета погрешностей используется материал приложения.

Лабораторная работа № 1 определенииe фокусных расстояний собирающей и рассеивающей линз

Цель работы: изучение основных законов геометрической оптики, определение фокусных расстояний рассеивающих и собирающих линз методом Бесселя и методом отрезков.

Основные теоретические положения

Так как длины световых волн, воспринимаемых глазом, очень малы (λ_св<1мкм), распространение света можно рассматривать, отвлекаясь от его волновой природы, и считать, что свет распространяется вдоль лучей.

В пределе λ→0 законы оптики возможно сформулировать на языке геометрии. Соответствующий раздел оптики называют геометрической (или лучевой) оптикой.

Основу геометрической оптики составляют три закона: закон прямолинейного распространения света в однородной среде, закон отражения света и закон преломления света.

Линза

Линза является простейшей центрированной оптической системой. Она представляет собой прозрачное тело, ограниченное, как правило, двумя сферическими поверхностями (или сферической и плоской поверхностью). Если толщина линзы вдоль оптической оси намного меньше радиусов кривизны, ограничивающих линзу поверхностей, линза называется тонкой. В обратном случае линзу называют толстой.

Линзы разделяются на два класса: собирающие (положительные) и рассеивающие (отрицательные). В случае, если коэффициент преломления вещества линзы больше коэффициента преломления среды, то собирающая линза имеет выпуклые сферические поверхности, а рассеивающая - вогнутые.

Рассмотрим тонкую собирающую линзу (рис. 1.1, а). На рисунке точка С - оптический центр, то есть точка, проходя которую, лучи не изменяют направления. Всякая прямая, проходящая через оптический центр, называется оптической осью, и если она, кроме того, проходит через центры кривизны - главной оптической осью (ось ОO'). Плоскость, перпендикулярная главной оптической оси и проходящая через оптический центр, называется главной плоскостью линзы

Главным фокусом линзы называется точка, в которой пересекаются после преломления в линзе лучи, падающие на нее пучком, параллельным главной оптической оси (на рис. 1.1 точка F). Расстояние между главным фокусом и оптическим центром линзы (расстояние CF=f') называется главным фокусным расстоянием и является основной характеристикой линзы. Для собирающих линз главное фокусное расстояние - величина положительная, так как находится справа от т. С в пространстве изображений. Для рассеивающих линз главный

Рис. 1.1. Построение изображений предмета АВ в собирающей (а) и рассеивающей (б) линзах

фокус является мнимым, так как для его отыскания берут не сами лучи, а их продолжение, поэтому фокус находится слева от С в пространстве предметов. Фокусное расстояние такой линзы - величина отрицательная (рис. 1.1, б).

Линзу характеризуют оптической силой D=1/f '. Эта величина измеряется в диоптриях (дптр - м^-1). У собирающей линзы D является величиной положительной, у рассеивающих линз - отрицательной.

Для построения изображения предмета с помощью линзы пользуются лучами, ход которых через линзу известен. Обычно берут два луча из следующих трех (рис. 1.1): луч 1, проходящий через оптический центр (он проходит через линзу, не преломляясь); луч 2, падающий на линзу параллельно ее главной оптической оси (этот луч при выходе из линзы пройдет через ее главный фокус); луч 3, проходящий через главный фокус линзы (он из линзы выйдет параллельно ее главной оптической оси).

Изображение предмета в зависимости от того, на каком расстоянии от линзы будет находиться предмет, может получиться увеличенным или уменьшенным, действительным или мнимым. Мнимым изображением предмета называется такое его изображение, которое находится перед линзой по одну сторону с предметом.

Обозначим через s (рис. 1.1) расстояние от предмета до т. С линзы, а через s' - расстояние от т. С до изображения. Формула, связывающая s, s' и f ', называется формулой тонкой линзы:

, (1.1)

где входящие расстояния являются алгебраическими величинами, знаки которых определяется правилом: если расстояние отложено в пространстве изображений (справа от т. С), то оно имеет положительный знак, если расстояние отложено в пространстве предметов (слева от т. C), то оно отрицательно.

Для рассеивающей линзы s, s' и f '<0, поэтому с учётом знаков формула не меняет свой вид. Для собирающей линзы s<0, s', f '>0, поэтому с учётом знаков формула приобретает вид:

, (1.2)

где s, s' и f ' - положительные расстояния.

Для толстой линзы формула (1.1) будет справедлива только в том случае, если за расстояние s (s') принять расстояние между предметом (изображением) до ближайшей преломляющей плоскости. В отличие от тонкой линзы, толстая линза является более сложной оптической системой, которая имеет две преломляющие плоскости H и H', называемые главными. У тонкой линзы главные плоскости Н и H' можно считать совпадающими и проходящими через центр линзы.

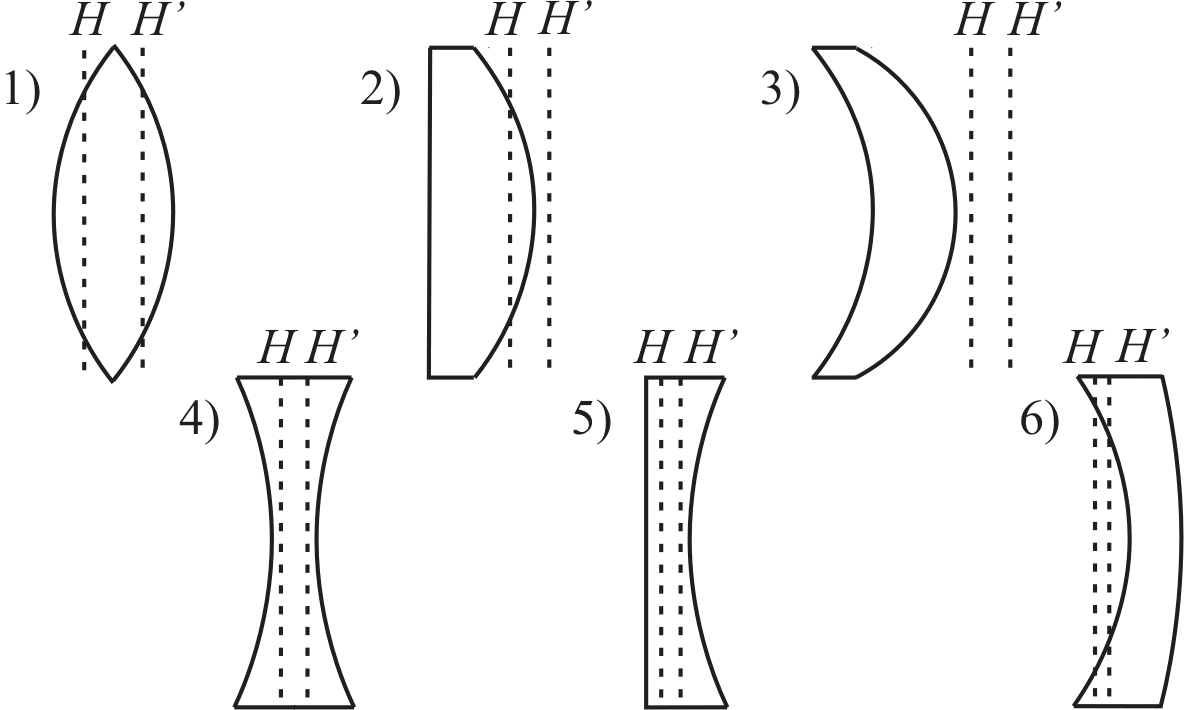
На рис. 1.2 представлены основные виды линз и положения главных плоскостей. Собирающие линзы: 1 - двояковыпуклая, 2 - плосковыпуклая,

3 - вогнуто-выпуклая (положительный мениск). Рассеивающие линзы: 4 - двояковогнутая, 5 - плосковогнутая, 6 - выпукло-вогнутая (отрицательный мениск). В зависимости от вида линзы главные плоскости и точки могут находиться как вне, так и внутри линзы, совершенно несимметрично относительно поверхностей, ограничивающих линзу, например, даже по одну сторону от неё.

Рис.1.2. Виды толстых линз а) б) Рис.1.3 Ход лучей в линзах

Метод определения фокусных расстояний топких линз - метод от­резков

Фокусное расстояние тонких линз можно определить методом, осно­ванным на измерении расстояний между предметом и линзой s, изображени­ем и линзой s' и при использовании формул (1.1) и (1.2) для тонких линз.

Способ измерения расстояний s и s' для собирающей линзы (рис. 1.3, а) основан па получении чёткого изображения предмета на экра­не при передвижении линзы между предметом и экраном.

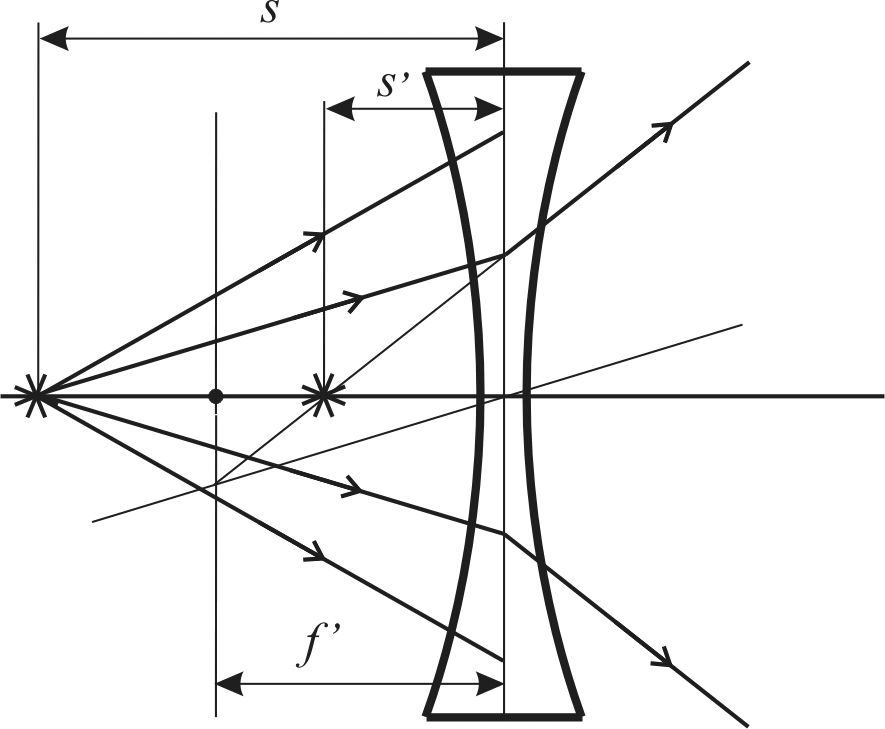
Измерение расстояний s и s' для рассеивающей линзы проводится иным способом, так как такая линза даёт только мнимое изображение предмета (рис. 1.3, б).

Первоначально собирается схема, как в случае соби­рающей линзы, и фиксируется координата ì экрана при наблюдении четко­го изображения предмета (рис. 1.4). Установка рассеивающей линзы меж­ду экраном и собирающей линзой приведёт к изменению положения чётко­го изображения, которое обнаруживают, отодвигая экран в положение с координатой ì'. При этом «предметом» для рассеивающей линзы служит изображение, полученное собирающей линзой. Повторно полученное изо­бражение уже является изображением, полученным с помощью рассеи­вающей линзы.

Рис. 1.4. Схема к методу измерения Рис. 1.5. Схема к методу Бесселя расстояний s и s' для рассеивающей линзы

Метод определения фокусных расстояний Бесселя

Воспользоваться формулами (1.1) и (1.2) для определения фокусного расстояния толстой линзы или системы линз затруднительно, поскольку все расстояния в случае толстых линз необходимо отсчитывать от соответ­ствующих главных плоскостей, положение которых, как правило, неиз­вестно.

Метод Бесселя позволяет найти фокусное расстояние, не зная по­ложения главных плоскостей линзы.

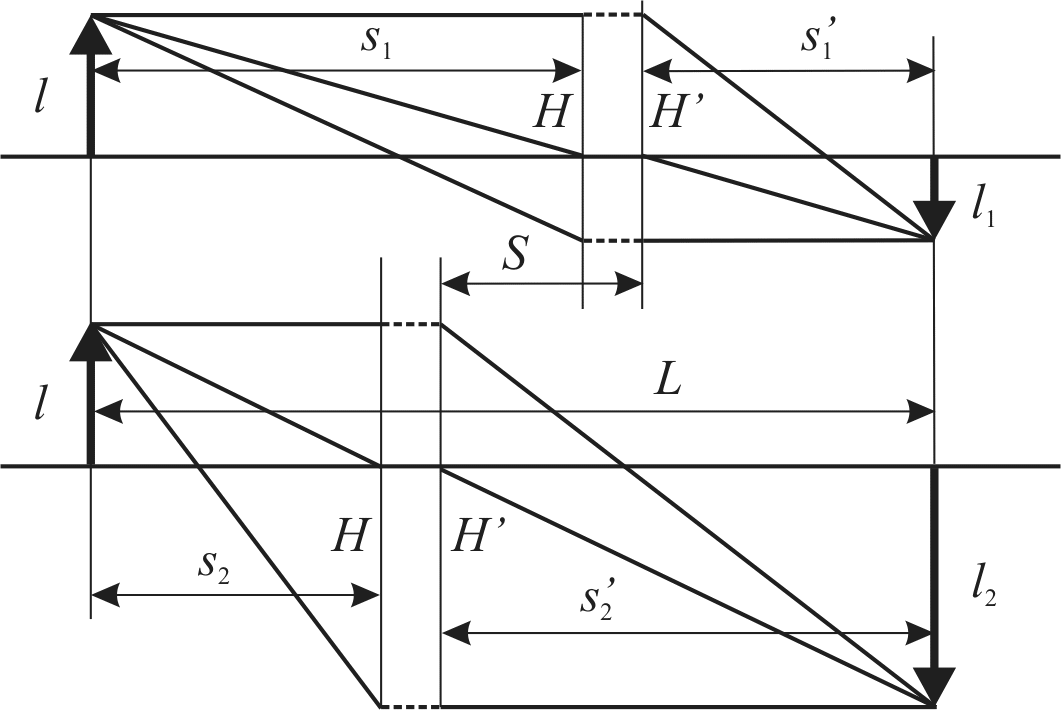
Между предметом и экраном поместим собирающую линзу. Зафикси­руем расстояние L между предметом и экраном. Если оно достаточно велико, существуют два положения линзы, при которых на экране получаются четкие изображения предмета - уменьшенное и увеличенное (рис. 1.5). Найдём эти положения, используя формулу (1.2) и следующее условие:

s+s' = L, (1.3)

в котором мы пренебрегаем расстоянием между главными плоскостями линзы по сравнению с L.

Здесь и далее расстояния s, s', L и f'- всегда по­ложительные величины.

Выразив расстояние s' из условия (1.3) и подставив в (1.2), получим квадратное уравнение относительно s, два решения которого соответствуют условию наблюдения чёткого изображения на экране:

s² –Ls+Lf = 0, (1.4)

где f ' заменили на f, так как |f|= |f'|.

Решения уравнения (1.4) существуют, если его дискриминант боль­ше нуля:

L²-4Lf ≥ 0, (1.5)

что имеет следующий смысл: четкое изображение на экране можно получить только, если расстояние от предмета до экрана превосходит фокусное расстояние линзы не менее чем в четыре раза.

Решения уравнения (1.4) симметричны относительно середины от­резка L:

. (1.6)

Тогда расстояние S между двумя положениями линзы, которым соответствуют увеличенное и уменьшенное изображения предмета, равно разности расстояний s₁-s₂:

. (1.7)

Из (1.7) получаем формулу для определения фокусного расстояния по методу Бесселя:

. (1.8)

Непосредственно с помощью метода Бесселя определить фокусное расстояние рассеивающей линзы невозможно, так как такая линза не дает действительных изображений предмета. Однако, если рассеивающую лин­зу (с фокусным расстоянием f_-) прижать вплотную к более сильной соби­рающей линзе (f'), получится собирающая оптическая система (f_c), оптиче­ская сила которой складывается из оптических сил образующих её линз:

, (1.9)

где оптическая сила рассеивающей линзы взята с отрицательным знаком.

Из (1.9) следует формула для расчета фокусного расстояния рассеи­вающей линзы:

. (1.10)