Экспериментальная установка и методика измерений.

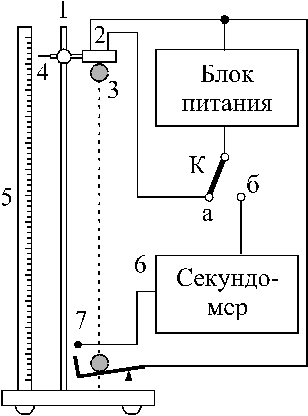
Экспериментально измерив время падения тела с высоты , можно, используя соотношение (2.10), рассчитать ускорение свободного падения.

О

Рис. 2.2. Экспериментальная установка

сновным конструктивным элементом установки (рис. 2.2) является штатив (1), по длине которого может перемещаться электромагнит (2), к которому притягивается шарик (3). Электромагнит снабжён указателем высоты шарика (4) по линейке (5). Время падения шарика определяется по секундомеру (6). В момент перевода ключа К – «Пуск» из положения (а) в положение (б) электромагнит отключается, шарик начинает падать и включается секундомер. Когда падающий шарик размыкает контакты (7) секундомер отключается.

Сначала на установке проверяется зависимость (2.10). Для этого шарик устанавливается на высоту и измеряется время его паденияс этой высоты. Затем высота меняется и измеряется время падения. Измерение повторяется несколько раз при разных значениях.

В следующем опыте определяется ускорение свободного падения. Для этого шарик поднимается на максимально возможную высоту и многократно измеряется время его падения с этой высоты.

Обработка результатов эксперимента

1. Выбрать различные пары измерений ,и рассчитать отношенияи.

2. Рассчитать погрешности измерений величин икак погрешности косвенных измерений по формуле

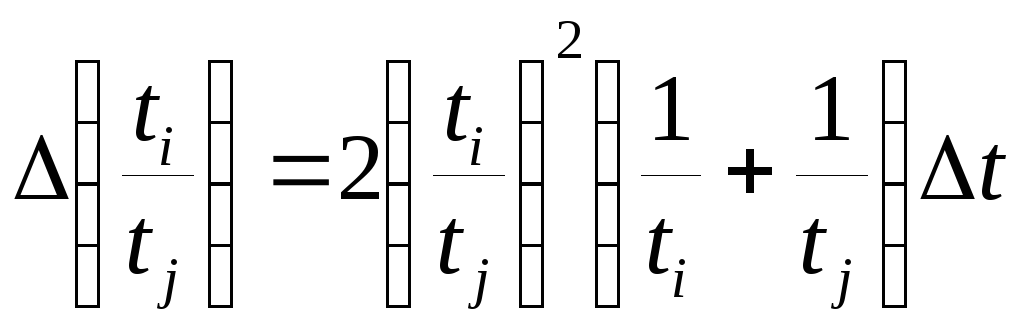, , (2.11)

где – систематическая погрешность измерения расстояния по линейке,– систематическая погрешность измерения времени по секундомеру.

3. Провести сравнение величин ипо формуле

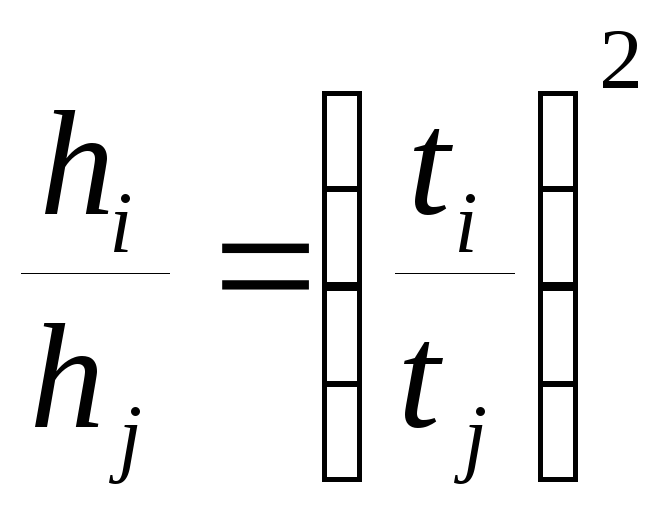(2.12)

с учётом рассчитанных в п. 2 погрешностей.

4. Ускорение свободного падения рассчитать по формуле

, (2.13)

где – среднее арифметическое значение времени падения,– количество измерений.

5. Рассчитать погрешность измерения величины как погрешность косвенных измерений по формуле

, (2.14)

где − случайная погрешность прямых измерений времени,

,

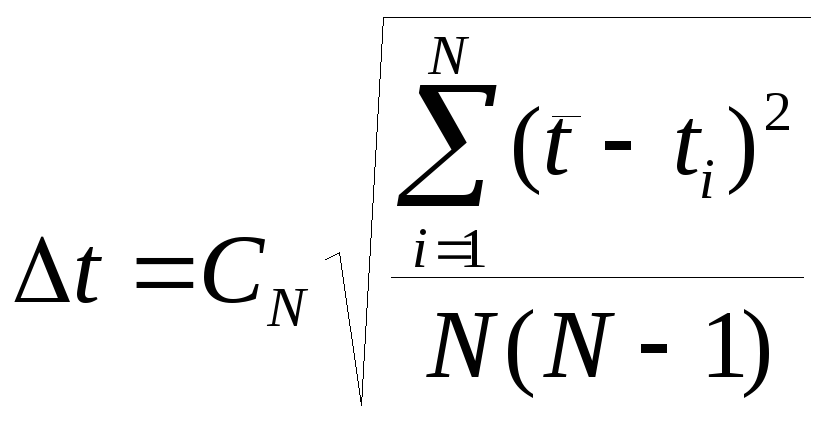где − коэффициент Стьюдента.

Лабораторная работа 3

Баллистический маятник

Цель работы: изучение закона сохранения импульса при неупругом ударе, определение скорости полета пули методом баллистического маятника.

Основные теоретические положения

Баллистический маятник представляет собой тяжелое тело, подвешенное на двойных нитях. В маятник стреляют по горизонтали пулей, которая застревает в нем. Пуля сообщает маятнику некоторую скорость, в результате чего маятник отклоняется. Измеряют величину отклонения маятника и по ней определяют скорость пули. Таким образом, методом баллистического маятника можно косвенно измерить скорость пули.

Если время соударения пули с маятником мало по сравнению с периодом колебаний маятника, то маятник не успевает заметно отклониться от исходного положения за время соударения. Это значит, что во время удара не возникнут силы, стремящиеся вернуть маятник в исходное положение, и систему пуля – маятник можно рассматривать как замкнутую. Удар пули, при котором она застревает в маятнике, является неупругим. При неупругом ударе выполняется закон сохранения импульса, который для системы из двух тел имеет вид

, (3.1)

где и− массы пули и баллистического маятника,искорости пули и маятника до удара,− скорость маятника с пулей после удара. Поскольку до удара скорость маятника была равна нулю, в левой части формулы (3.1) останется только первое слагаемое. Направим осьвдоль скорости движения пули и спроектируем формулу (3.1) на ось:

. (3.2)

После удара маятник с пулей будет двигаться по дуге радиуса , где− длина нитей подвеса, и поднимется на некоторую высоту. Вследствие действия силы тяжести скорость системы «маятник-пуля»и ее кинетическая энергия будут убывать до нуля. Потенциальная энергия системы наоборот будет возрастать. За нуль отсчета потенциальной энергии примем вертикальную координату центра масс маятника перед выстрелом пули.

Кинетическая энергия системы сразу после удара пули равна , потенциальная энергия системы при ее отклонении до высотыравна. Для системы маятник-пуля после удара применим закон сохранения механической энергии, на основании которого можно записать

(3.3)

Из уравнений (3.2) и (3.3) выразим скорость пули

(3.4)

Поскольку масса пули во много раз меньше массы маятника, величиной в числителе формулы (3.4) по сравнению с величиной_, можно пренебречь и получить формулу для расчета скорости пули в следующем виде:

. (3.5)

П

Рис. 3.1. Баллистический маятник

роизводить непосредственное измерение высотыне всегда удобно, но ее можно определить либо по горизонтальному отклонению, либо по углу поворота маятника после попадания пули. Пусть маятник с застрявшей пулей отклонился на уголот вертикали.

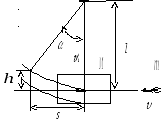
Из рис. 3.1 видно, что высота отклонения выражается через угол отклонения следующим образом:

, (3.6)

при условии, что угол мал, примем, что

С учетом этого скорость пули из формулы (3.4) выражается следующим образом:

(3.7)

Выразим высоту подъема центра масс маятника через величину его отклонения по горизонтали. Используем для прямоугольного треугольника, изображенного на рис.3.1.,теорему Пифагора и запишем. Раскроем скобки в левой части; примем, что величинамала по сравнению с другими слагаемыми и тогда получим, откуда. Таким образом скорость пули может быть выражена через горизонтальное отклонение маятника по формуле

. (3.8)

М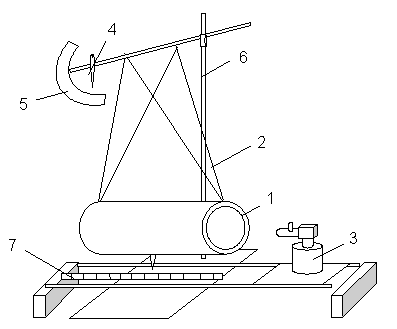етодика эксперимента

У

Рис. 3.2. Схема экспериментальной установки

становка состоит из штатива 6, на котором на двойном подвесе 2 закреплен баллистический маятник 1 в виде трубки, заполненной ватой (рис.3.2). Напротив открытого конца трубки на той же высоте располагается пистолет 3. Для измерения угла отклонения маятника после попадания в него пули служат стрелка 4 и транспортир 5. К корпусу маятника прикреплен указатель, позволяющий контролировать отклонение маятника по горизонтали. Измерение горизонтального отклонения производится по линейке 7, которая крепится к подставке.

Последовательность выполнения работы.

1 способ. Определение скорости по измерению угла отклонения маятника.

Отмечают положение стрелки 4 на шкале транспортира 5 – начальный угол . Из пистолета 3 делают выстрел, замечают положение стрелки 4 при отклонении маятника – записывают значение.

Определяют угол отклонения маятника .

Опыты проводятся с двумя пулями массами и. Для каждой пули производится 5−6 выстрелов.

2 способ. Определение скорости по измерению горизонтального отклонения маятника. По линейке 7 отмечают начальное положение указателя. Производят выстрел, маятник отклоняется. Отмечают его положение при отклонении.

Определяют перемещение маятника по горизонтали .

Опыты проделывают 5−7 раз с двумя пулями разной массы. Масса баллистического маятника и массы пульуказаны на лабораторной установке.

Обработка результатов эксперимента

1. Вычислить последовательно средние значения величин ,.

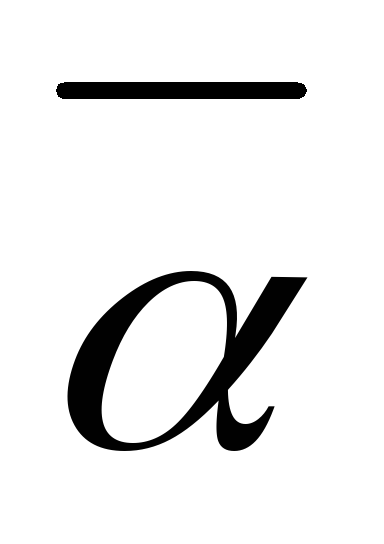2. Величину вычислить по формуле (3.8), в которо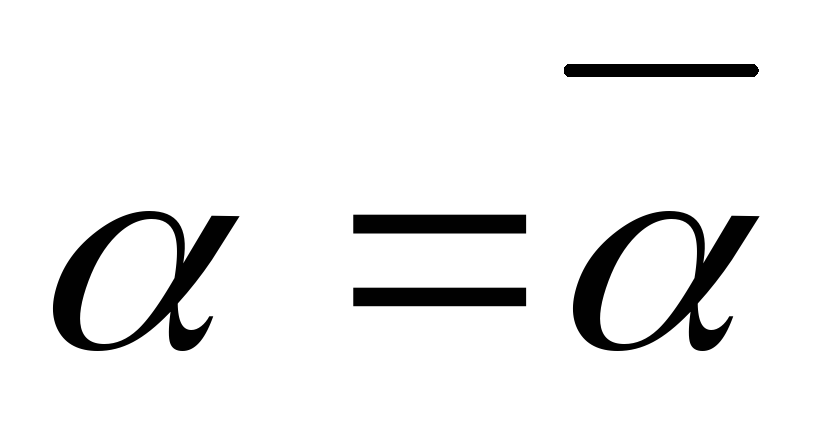йили.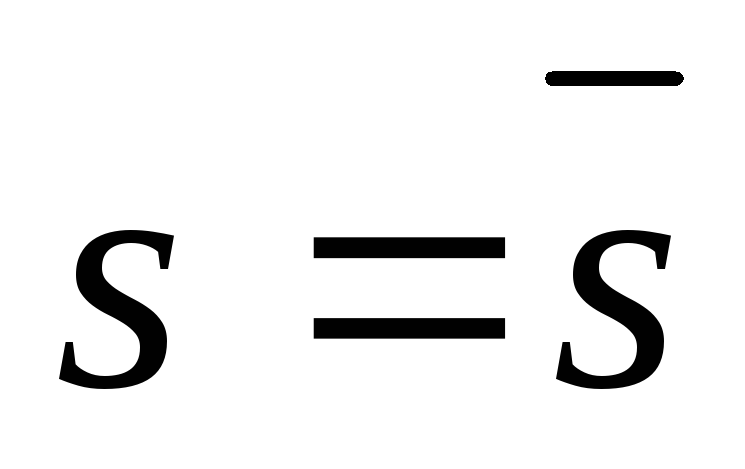

Для второй пули производятся такие же расчеты.

Расчет погрешностей.

1. Погрешность косвенных измерений скорости пули, выполняемых первым способом, рассчитывается по формуле

. (3.9)

В (3.9) входит погрешность прямых измерений угла

, (3.10)

где − коэффициент Стьюдента,− среднее квадратичное отклонение.

2. Погрешность косвенных измерений скорости пули, выполняемых вторым способом, рассчитывается по формуле

. (3.11)

В этом случае погрешность прямых измерений отклонения маятника по горизонтали находят по формуле

. (3.12)

3. Результат для каждого способа представить в виде:

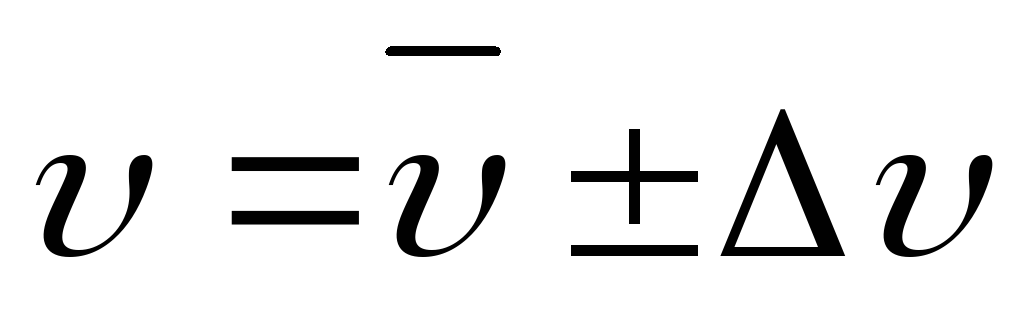
Дополнительное задание: Определение скорости пули по дальности полета при горизонтальной стрельбе.

Движение тела, брошенного горизонтально с некоторой высоты, представляет собой два одновременных движения: равномерное по горизонтали и равноускоренное по вертикали с ускорением, равным ускорению свободного падения (рис. 3.3).

Дальность полета, то есть перемещение по горизонтали определяется по формуле. _. Время движения тела зависит от высоты точки бросания и связано с ней формулой . Отсюда выражаем время полетаи затем дальность полета.

Т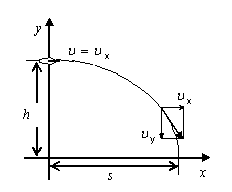аким образом скорость полета пули может быть рассчитать по формуле

Рис. 3.3 Принцип независимости движений.

. (3.13)

Методика эксперимента

В этом задании используется только пистолет 3, который разворачивают к краю стола, чтобы пуля не попадала в маятник.

Измеряют высоту пистолета над столом . После выстрела определяют дальность полета пули− расстояние, которое она пролетела по горизонтали. Для измерений используют линейку 8. Опыт проводят 3−5 раз.

Проводят измерения дальности полета для двух других значений высоты пистолета ,.

Обработка результатов эксперимента

1. Для каждого значения высоты пистолета над столом находят среднее значение дальности полета ,,и рассчитывают среднее значение скорости пули по формуле

. (3.14)

2. Определяют погрешность прямых измерений дальности полета по формуле

. (3.15)

3. Находят случайную составляющую погрешности косвенных измерений скорости пули:

. (3.16)

4. Приборную погрешность величины скорости , связанную с измерением величины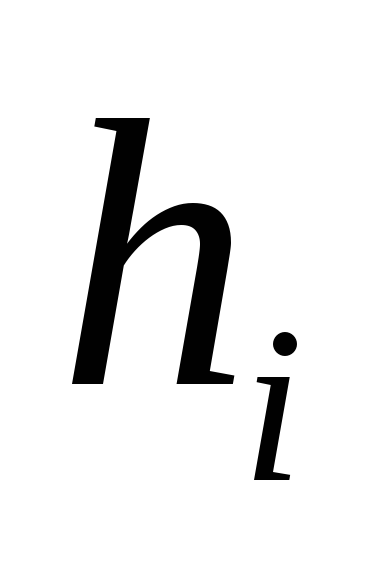, рассчитать по формуле

. (3.17)

5. Суммарную погрешность косвенных измерений величины определить по формуле:

. (3.18)

6. Результат представить в виде: .

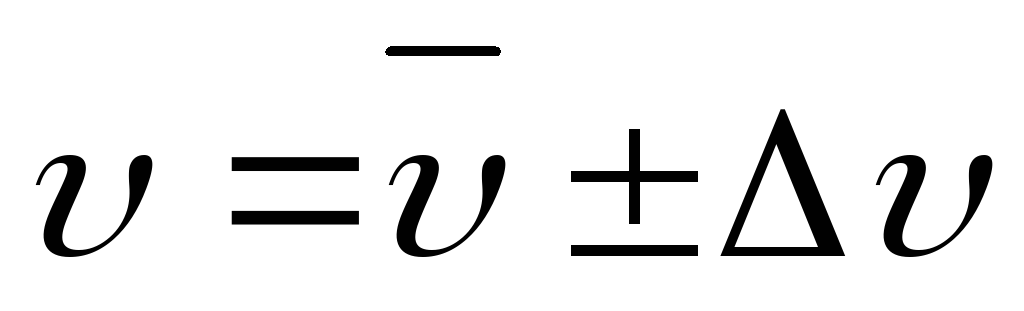Лабораторная работа 4