Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский Государственный Технический Университет им. Ю.А. Гагарина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Posobb

.pdf

Скачиваний:

Добавлен:

12.02.2015

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

	21(k )	23 (k )
	21(k )	23 (k )
где: (k ) 1	31(k )	33 (k )	,	k ik	(5.44)

	21(k )	22 (k )
	21(k )	22 (k )
	31(k )	32 (k )

Так как (ik), 1,k и eik t есть комплексные сопряженные, то с учетом (5.20) из (5.43) получаем колебания полярного угла (t) выходной точки упругого звена манипулятора

	1	N
(t)		a0(0) (Re (ik ))ak (Im (ik ))bk cos k t
	2
		k	1

N
(Re (ik ))bk			(Im (ik ))ak sin k t	(5.45)

k 1

Согласно (5.42) в случае многочастотных автоколебаний

a0 a0(q) ,

a a(q) ,	b 0 ,	a	a(q) ,	b b(q) ,	k 2,3,..., N	(5.46)
1 1	1	k	k	k k

Вводя (5.46) в (5.45), находим автоколебания выходной точки упругого звена манипулятора

(t)		1	a(q)(0) (Re (ik ))a(q) cost
(t)			a(q)(0) (Re (ik ))a(q) cost
		2	0	1
	N (Re (ik ))a(q) (Im (ik ))b(q) cos k t				(5.47)
			k	k
	k 2
	N (Re (ik ))b(q) (Im (ik ))a(q) sin k t
			k	k

k 2

Здесь согласно (5.44), (5.14), (5.13) и (2.24) имеем (0)=1.

Если отсутствуют предельные циклы функции 1(t), то функция (t) также не имеет предельных циклов.

5.5. Устойчивость автоколебаний в одномерной нелинейной КДС

Положим, что в рассматриваемой нелинейной КДС (5.7) возникли периодические колебания, и согласно (5.18) имеем

N						N
	( k ) 1,k e k t p0 A( k ) fk e k t 0 , k=ik
k N						k N
		1	a ib		,		1	a ib		,
			a ib		,			a ib		,
1,k		2	k	k	1, k		2	k	k
		2					2

121

fk 1, N ,

, ,1,N

,1,0

1,m e mt

e ik t dt ,

(ck

isk ) ,

m N

f k 12 (ck isk ) .

Тогда для каждой k-той гармоники следует

D (

)

e k t

(5.48)

1,k

где:

Dk ( k ) ( k ) p0 A( k )

(5.49)

1,k

ck ak sk bk

1,k

ck bk

ak sk

k N ,...,0,..., N

Легко видеть, что формально Dk(k) представимо в виде характеристического квазимногочлена однородного уравнения (5.48). Для того, чтобы

периодические колебания 1,k eik t , k= –N,…,0,…,N в системе (5.48) были незатухающими, необходимо и достаточно, чтобы система была на границе

устойчивости, то есть частотные годографы Dk(ik ) проходили на комплексной плоскости ReDk+ iImDk через начало координат (0,0). Следовательно, получаем уравнения

Dk (ik ) (ik ) p0 A(ik ) k i k 0 , k N,...,0,..., N , (5.50)

определяющие 2N+1 характеристик (q) ,a0(q) ,a1(q) ,a2(q) ,b2(q) ,...,aN(q) ,bN(q) автоко-

лебаний.

Ранее мы получили характеристики (5.41) периодических автоколебаний (5.42). Подставляя (5.41) в (5.50) и проводя вычисления, убеждаемся, что (5.41) удовлетворяет уравнениям (5.50). Проверим далее, являются ли

автоколебания (5.42) устойчивыми.

Так как (ik), A(ik),k i k являются комплексными сопряженны-

ми при k>0 и k<0, то годографы Dk(ik ) и D-k(-ik ) на комплексной плоскости будут симметричны относительно действительной оси. Поэтому бу-

дем далее полагать k 1, N ; 0.

Подставляя известные из (5.41) характеристики

a0(q) ,a1(q) ,a2(q) ,b2(q) ,...,aN(q) ,bN(q) в (5.50) с учетом (5.49), (5.20) при 0, находим

Dk (ik ) (ik ) p0 A(ik ) k(q) i k(q) ,

122

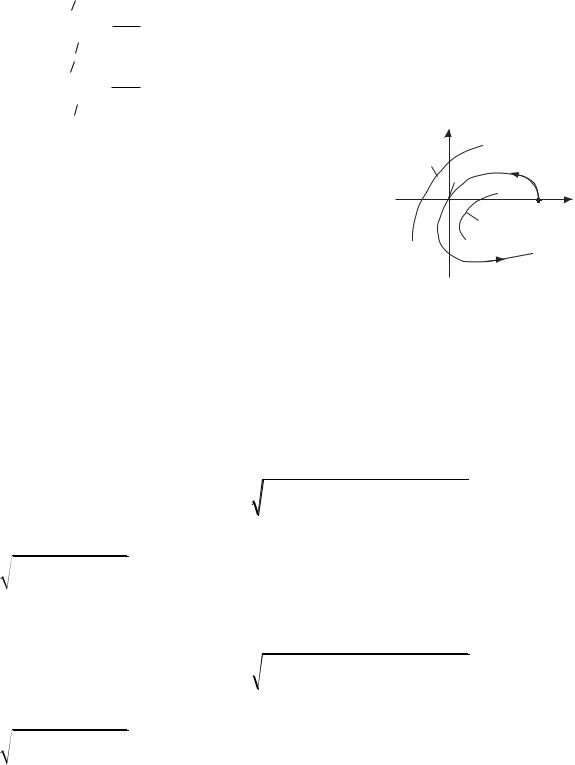
(q)	c(q)a(q) s(q)b(q)			(q)	c(q)b(q)	a(q)s(q)
	k k	k k	,		k k	k k	,	(5.51)
	ak(q) 2 bk(q) 2				ak(q) 2	bk(q) 2
k				k


	ck(q)




	sk(q)

a(q)

f 0

a(q)

f 0

am(q) m 1


cos m t bm(q) sin m t cos k t dt	,



cos m t bm(q) sin m t sin k t dt ,	k 1, N

Рассмотрим колебания системы на k-той

iImDk

гармонике, то есть с частотой k , где k пробега-

(q )

ет значение

1,2,…,N. Изменяя

от

0 до ,

годограф Dk(ik )

строим частотный

на ком-

ReDk

плексной плоскости (ReDk, iImDk) (рис. 5.1)

при постоянных a1(q) ,...,aN(q) ,bN(q) const

и убеж-

Dk(ik )

даемся, что годограф проходит через точку

(0,0) при =(q), то есть D (ik (q) ) 0,

k 1, N

Рис. 5.1

Принимая a(q) a , b(q) b ,

b 0 , строим кривую воз-

мущенного годографа D(1)

[ik((q) )] в окрестности точки =(q), а за-

тем при a(q)

a , b(q) b , строим кривую D(2)

[ik((q) )].

Если кривая D(1)

занимает положение 1 (рис. 5.1) и охватывает точку

(0,0), то согласно теореме 3.5 квазимногочлен D(1)

[ik((q) )] является

устойчивым . Тогда амплитуда

ak(q) ak 2

bk(q) bk 2 колебаний

ak(q) ak cos k t bk(q) bk sin k t должна затухать до величины

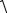
ak(q) 2 bk(q) 2 .

Если кривая Dk(2) занимает положение 2 (рис. 5.1) и не охватывает точку (0,0), то квазимногочлен Dk(2) [ik((q) )] в соответствии с теоремой

3.5 неустойчивый и амплитуда ak(q)

ak(q) ak cosk t bk(q) bk sin k t

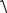
ak(q) 2 bk(q) 2 .

ak 2 bk(q) bk 2 колебаний увеличится до величины

Следовательно, в рассматриваемом случае на k-той гармонике установится предельный цикл ak(q) cos k (q)t bk(q) sin k (q)t .

123

Если же кривая D(2)

при a(q)

a ,

b(q) b

занимает положение 1

(рис. 5.1), то амплитуда

ak(q) ak 2 bk(q)

bk 2

уменьшится до нуля и

автоколебания на k-той гармонике будут отсутствовать.

Если кривая D(1)

при a(q) a , b(q)

занимает положение 2 (рис.

5.1), то амплитуда

ak(q) ak 2

bk(q) bk 2 будет увеличиваться и пре-

дельный цикл на k-той гармонике окажется неустойчивым.

Замечание 5.3. Если, например,

(q)

0 ,

(q)

n 2

то в системе установятся смещенные автоколебания выходного сигнала

следящего привода на первой гармонике

a(q)

a(q) cost

(5.52)

Вводя (5.52) в (5.47), находим автоколебания выходной точки упругого

звена манипулятора

(t)

a(q) (Re (i ))a(q) cost

5.6. Метод гармонического баланса в высоких приближениях применительно к многомерным КДС

Известна многомерная линейная КДС в форме (4.36) обобщенной динамической модели

[ M m( ) 2 K k() C c() ]y() B b() x()

Если предположить режим установившихся вынужденных колебаний,

то =i,	x (x ,..., x ) x(i ) (x				,..., x	)ei t ,
	1	a		1	a
				m	m
y ( y ,..., y ) y(i ) ( y				ei( t 1 ( )) ,...., y			ei( t b ( )) ) .
1	b		1		b
			m			m
Следовательно,
[ M m(i ) (i )2			K k(i ) (i ) c(i )]y Cy B b(i ) x (5.53)

Перейдем далее к многомерной нелинейной КДС. Будем под символом C понимать нелинейный оператор вида

C110

C120

C10b

f1( y1)

Cy C0 f ( y) ,

( y

)

, (5.54)

f ( y)

( yb )

Cb1

Cb2

Cbb

Здесь C0 – матрица коэффициентов упругой жесткости, f(y) – матрица нелинейных безинерционных характеристик.

124

Пусть x 0 и предположим, что в системе установились самовозбуждающиеся периодические движения y(t) c периодом 2/. Представим y(t) и f(y(t)) в виде N – ых частичных сумм рядов Фурье в комплексной форме

yk eik t ,

( y1,k , y2,k ,..., yb,k ) ,

(5.55)

k N

n,k

(t)e ik t dt ,

n 1,b ,

) ,

)

– комплексно сопряженные,

n,k

n, k

n,k

f ( y)

fk ( y N ,..., y0 ,..., yN )eik t

, fk

( f1,k , f2,k ,..., fb,k ) ,

k N

fn,k ( y N

,..., y0 ,..., yN )

fn ym eim t e ik t dt ,

n 1,b

;

m N

) ,

)

– комплексные сопряженные.

n,k

n, k

n,k

Тогда согласно (5.53) – (5.55) при x=0 имеем

G* (ik ) yk eik t C0 fk

eik t 0

(5.56)

k N

где

G* (ik ) [ M m(ik ) (ik )2

K k(ik ) (ik ) c(ik )] [G*jn (ik)] ,

j,n 1,b

(5.57)

Так как в выражении (5.56) под знаком приведены величины при k>0 и k<0 комплексные сопряженные, то из (5.56) следует

G* (ik ) y

eik t

Re f

eik t

0 ,

k N

то есть

G* (0) y C0 f

Re G* (ik ) y

eik t

2C0

Re f

eik t

(5.58)

k 1

Согласно принятой форме записи

k N

		a0	N
yk	eik t	a0	(ak cos t bk sin t)	,	(5.59)
yk	eik t		(ak cos t bk sin t)	,	(5.59)
	2		k 1
			k 1

(a ib ), y

(a ib ),

b 0 ,

ak (a1,k , a2,k ,...,ab,k ),

bk (b1,k ,b2,k ,...,bb,k ),

a0 (a1,0 , a2,0 ,...,ab,0 ),

f ( y) fk

eik t

(ck cos t sk sin t)

k N

k 1

125

f ( y) ( f1( y), f2 ( y),..., fb ( y)),

fk ( y) ( f1,k , f2,k ,..., fb,k )

ck (c1,k

, c2,k ,...,cb,k ) ,

sk (s1,k

, s2,k ,..., sb,k ) , s0 (s1,0

, s2,0 ,...,sb,0 ) ,

am cos m t bm sin m t dt c0 (a0

,a1,b1,...,aN ,bN ) ,

m 1

am cos m t bm sin m t cos k t dt

m 1

ck (a0 ,a1,b1,...,aN ,bN )

am cos m t bm sin m t sin k t dt

m 1

sk (a0 ,a1,b1,...,aN ,bN ) ,

) ,

)

, s =0 .

n,k

n, k

n,k

Из (5.58) с учетом (5.59) имеем

G* (0)a

C0c

Re G* (ik )(a

ib ) cos k t

k 1

Im G* (ik )(a

ib ) sin k t

cos t s

sin t) 0

k 1

Приравнивая в правой и левой частях данного равенства коэффициенты

при cos k t

и sin k t , k=0,1,2,…,N, а также полагая b1,1=0, получаем систе-

му нелинейных уравнений для определения неизвестных и 2N+1 неиз-

вестных векторов a0, a1, b1,…, aN, bN в форме

( ) (ReG* (ik ))a (ImG* (ik ))b

C0c (a

,a ,b ,...,a

,b ) 0 ,

(5.60)

1 1

N k

( ) (ReG* (ik ))b

(ImG* (ik ))a

C0s (a

,a ,b ,...,a

,b ) 0 ,

1 1

( ) G* (0)a C0c (a ,a ,b ,...,a

,b ) 0 ,

2 N 1

0 1 1

( ,a0 ,a1,b1,a2 ,b2 ,...,aN ,bN ), b1,1

0 ,

k 1, N .

Так как k( ), N+k( ),2N+1( ) являются b-мерными вектор-функциями, а

искомые a0, a1, b1, a2, b2,…, aN, bN являются b-мерными векторами, то есть
k ( ) ( 1,k ( ), 2,k ( ),..., b,k ( )) ,

N k ( ) (1,N k ( ),2,N k ( ),..., b,N k ( )),		k 1, N ,
2 N 1( ) ( 1,2 N 1( ), 2,2 N 1( ),..., b,2 N 1( )) ,
a0 (a1,0 ,a2,0 ,..,ab,0 ),	a1 (a1,1,a2,1,..,ab,1),	b1 (b1,1,b2,1,..,bb,1),

………………………………………………………………………

126

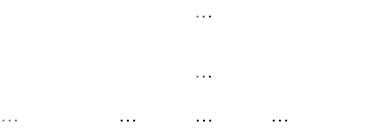
aN (a1,N ,a2,N ,..,ab,N ), bN (b1,N ,b2,N ,..,bb,N ) ,

то полагая b1,1=0, перепишем уравнения (5.60) в форме системы (2N+1)b скалярных уравнений

b	b	b
j,k ( ) ReGjn (ik ) an,k ImGjn (ik ) bn,k C0jncn,k ( ) 0 ,
n 1	n 1	n 1
b	b	b
j, N k ( ) ReGjn (ik ) bn,k ImGjn (ik ) an, k C0jnsn, k ( ) 0,
n 1	n 1	n 1
b	b
j,2 N 1( ) G*jn (0)an,0	C0jncn,0 ( ) 0 ,		(5.61)
n 1	n 1
=(a0, a1, b1, a2, b2,…, aN, bN)=
=( a1,0 , a2,0 ,…, ab,0 , a1,1 , a2,1 ,…,ab,1 , b2,1 ,…, bb,1 ,…,
a1,N , a2,N ,…,ab,N , b1,N , b2,N ,…,bb,N),		b1,1=0,
=( , )=( , a1,0 , a2,0
=( , )=( , a1,0 , a2,0	,…, ab,0 ,…, b1,N , b2,N ,…,bb,N), j 1,b;		k 1, N .

Система уравнений (5.61) является замкнутой, так как число уравнений и число искомых компонент вектора совпадают и равны (2N+1)b.

Вводя в рассмотрение вектор-функцию

( )=( 1,1( ), 2,1( ),…, b,1( ), 1,2( ), 2,2( ),…, b,2( ),…, 1,N+1( ),

2,N+1( ),…, b,N+1( ), 1,N+2( ), 2,N+2( ),…, b,N+2( ),…, b,2N+1( )) ,

запишем систему нелинейных уравнений (5.61) в форме одного векторного уравнения

( )=0

(5.62)

По аналогии с выражением (5.26) запишем формулу вычисления корней уравнения (5.62) по методу Ньютона

( g 1) ( g ) W 1( ( g ) ) ( ( g ) ),

g 0,1,2,...

(5.63)

( ( g ) )

1,1

a1,0

bb,N

( ( g ) )

2,1

W ( ( g ) ) ( ( g ) )

a1,0

bb,N

( ( g ) )

...

( ( g ) )

b,2 N 1

a1,0

bb,N

(5.64)

В качестве нулевого приближения (0) примем решение по методу гар-

монической линеаризации. Полагая N=1 и

(

,a0 ,a1,b1) (,a1,0 ,...ab,0 ,a1,1,...,ab,1,b2,1,...,bb,1)

, находим из (5.61)

векторное уравнение метода гармонической линеаризации

127

(

) 0 ,

(5.65)

(

) (1,1(

), ..., b,1( ), 1,2 ( ),...,b,2 ( ),1,3( ),...,b,3( )) ,

j,1(

) ReG*jn (i

) an,1 ImG*jn (i

) bn,1 C0jncn,1(

) ,

n 1

n 2

n 1

) ImG*jn (i

) an,1 ReG*jn (i

)

j,2 (

bn,1 C0jn sn,1(

) ,

n 1

n 2

n 1

) G*jn (0) an,0

C0jncn,0 (

j,3 (

) 0 ,

j 1,b ,

n 1

) ,

(a1,0 ,...ab,0 ,a1,1,...,ab ,1,b2,1,...,bb ,1 )

(

Корень векторного уравнения (5.65) вычисляем по методу Ньютона

( g )

g 0,1,2,...

( g 1)

W 1(

( g ) ) ( ( g) ),

(5.66)

( g ) )

(

( ( g ) )

1,1

a1,0

bb,1

(

( g ) )

(

2,1

W ( ( g ) )

a1,0

bb,1

( g ) )

(

( g ) )

(

b,3

a1,0

bb,1

Если для любого сколь угодно малого вещественного 3b-мерного век-

( , ,..., ) ,

>0 в процессе вычислений определяется такое целое

тора

положительное число p>0, что

g p :

W 1(

( g ) ) ( ( g ) )

, то процесс

Ньютона сходится и с погрешностью O(

) можно принять корень

,...,a

,a ,...,a

,...,b

) ( p)

(5.67)

(

1,0

b,0

1,1

b,1

2,1

b,1

Далее найдем решение по методу гармонического баланса в высоких приближениях. Используя (5.67), запишем нулевое приближение (0) искомого корня векторного уравнения (5.62) в виде

(0)	((0) ,a(0)						,a(0) ,b(0)					,...,a(0)		,b(0) ) ,											(5.68)
				0				1	1				N		N
где	(0)			,			a(0)		a			(a ,a ,...,a							),	a(0)	a (a		,a	,...,a	),
								0	0			1,0			2,0	b,0				1	1	1,1	2,1	b,1

b(0)		b	(0,			b		,...,b			), a(0)			b(0)		0,			2,3,..., N
1	1			2,1						b,1
Вводим (5.68) в процесс Ньютона (5.63). Если существует целое поло-
жительное число q>0 такое, что при вычислениях
															, где:			( , ,..., )				и >0 – наперед за-
g q :					W 1( ( g ) ) ( ( g ) )									q	, где:		q	( , ,..., )				и >0 – наперед за-
														q			q

данное сколько угодно малое положительное число, то последовательность

128

приближений Ньютона (5.63) сходится. Следовательно, с погрешностью O(q ) примем корень

(q) ((q) ,a(q) ,a(q) ,b(q) ,a(q) ,b(q) ,...,a(q) ,b(q) ) ,								(5.69)
		0 1	1	2	2	N	N
a(q) (a(q) ,...,a(q) ),...,			b(q) (b(q) ,...,b(q)			),	b 0
0	1,0	b,0	N	1,N	b,N		1,1

Если не существует корня (5.69) векторного уравнения (5.62), то есть не существует совокупности (2N+1)b действительных чисел

(q) 0, a(q) ,	a(q) ,...,	b(q)	, удовлетворяющих системе уравнений (5.61),
1,0	2,0	b,N

то в рассматриваемой нелинейной многомерной КДС будут отсутствовать предельные циклы (автоколебания).

Пусть существует корень (5.69), элементами которого являются действительные числа

(q) 0, a(q) ,...,	a(q) ,	a(q) ,...,a(q) ,...,b(q) ,...,b(q) ,...,				b(q) ,...,b(q)		(5.70)
1,0	b,0	1,1	b,1	1,2	b,2	1,N	b,N

Тогда, если выполняются условия устойчивости автоколебаний, то в системе установятся периодические автоколебания с базовой частотой (q) и с высшими гармониками до N-ых включительно

y(q)

k 2

(q)

a(q)

1(q)

1,0(q)

1,1(q)

(q)

a2,0

a2,1 cos(q)t b2,1

(q)

ab,0

ab,1

bb,1

a(q)

b(q)

1,(qk)

a2,k

cos k (q)t b2,k sin k (q)t

(q)

k 2

(q)

ab,k

bb,k

sin (q)t (5.71)

5.7. Устойчивость автоколебаний в многомерной КДС

Определим устойчивость автоколебаний в рассматриваемой многомерной КДС. Положим, что в системе возникли периодические колебания (5.55). Тогда согласно (5.56) имеем

G* (ik ) yk

C0 fk eik t

(5.72)

k N

yk ( y1,k , y2,k ,..., yb,k ),

fk ( f1,k , f2,k ,..., fb,k )

) , y

)

n,k

n, k

n,k

fn,k

fn ym eim t

e ik t

dt ,

m N

129

) , f

) ,

n,k

n, k

n,k

G* (ik ) [G*

(ik )],

C0 [C0 ] ,

j 1,b;

n 1,b

Из (5.72) для каждой k-той гармоники следует

G* (ik ) yk

C0 fk eik t 0 ,

k=-N,…,0,…,N,

то есть

G*jn (ik ) yn,k C0jn fn,k eik t

k N ,...0,..., N ,

j 1,b

(5.73)

n 1

Вводя

G* (ik) из (5.57) в (5.73) и обозначая =ik , получаем

( )e k t

D(k )

j 1,b

(5.74)

D(k ) ( )

( )) 2 (K

( )) c

( ) y

n,k

j k

n 1

–N,…,0,…,N

(5.75)

Для того чтобы периодические колебания в системе однородных уравнений (5.74) на k-тых гармониках были незатухающими, необходимо и до-

статочно,	чтобы среди корней характеристических	квазимногочленов

D(k ) ( ),	j 1,b были чисто мнимые корни. То есть система (5.74) долж-
j k

на быть на границе устойчивости и частотные годографы		D(k ) (ik ), j	1,b
		j

должны проходить через начало координат (0,0) на комплексной плоскости

Re D(k ) (ik ) i Im D(k ) (ik) . Отсюда следуют (2N+1)b уравнений

D(k )

(ik )

(ik ))(ik )2 (K

(ik ))(ik ) c

(ik ) y

n,k

n 1

C0jn fn,k 0,

j 1,b;

k N,...,0,..., N,

(5.76)

определяющие (2N+1)b характеристик автоколебаний

(q) , a1,0(q) ,..., ab(q,0) ,

a1,1(q) ,...,ab(q,1) , b2,1(q) ,..., bb(,1q) ,...,b1,2(q) ,...,bb(,2q) ,...,

b1,( qN) ,...,bb(,qN)

Ранее мы определили по методу Ньютона характеристики (5.70) периодических автоколебаний (5.71). Подставляя числа (5.70) в уравнения (5.76), проверяем, удовлетворяют ли они уравнениям (5.76). Если не удовлетворяют, то в вычислениях имеется ошибка. Если удовлетворяют, то далее исследуем автоколебания (5.71) на устойчивость.

Так как выражения D(jk ) (ik) и D(jk ) (ik) являются комплексно со-

пряженными при >0, то их годографы на комплексной плоскости будут симметричны относительно действительной оси. В силу этого положим да-


лее k 1, N;			0
130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.07.2019318.98 Кб8Part_08_M.doc
#
25.11.2018144.38 Кб6Part_11_M.doc
#
25.11.2018124.93 Кб5Part_12_M.doc
#
01.04.2025147.58 Кб0Pogorazdov_-_Formoobrazovanie.docx
#
01.05.202584.15 Кб0Poluchenie_chistykh_metallov_1.docx
#
12.02.20152.64 Mб59Posobb.pdf
#
12.02.2015303.72 Кб7Power supply - term paper.pdf
#
01.05.2025903.17 Кб0Poyasnitelnaya_zapiska_Egorova_N_S (1).doc
#
01.05.202599.51 Mб0Poyasnitelnaya_zapiska_Luzakin_A_A.doc
#
01.05.2025903.17 Кб0Poyasnitelnaya_zapiska_Tryasogolov_I_A_kopia (1...doc
#
12.02.20151.6 Mб205Praktikum_ekologii.doc