
ЭЛМ_Презентация_16
.pdf
Коэффициенты взаимной индуктивности
Взаимная индуктивность численно равна магнитному потоку сквозь один из контуров, создаваемому единичным током в другом контуре.
Коэффициенты 12 и 21 зависят от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающий контуры среды.
Расчёт и эксперимент подтверждают, что при отсутствии ферромагнетиков 12 = 21. Это теорема взаимности.
Следовательно, магнитный поток 1 сквозь контур 1 созданный током , текущем в контуре 2, равен магнитному потоку 2 сквозь контур 2, созданному таким же током , текущем в контуре 1.
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
5/34

Э. Д. С. взаимной индукции
Явление взаимной индукции заключается в возникновении Э. Д. С. индукции в одном из контуров при изменении тока в другом.
|
1 |
2 |
|
|
2 |
|
1 |
|
E1 = − |
|
= − 12 |
|
, |
E2 = − |
|
= − 21 |
|
|
|
|
|
|||||
Будем предполагать, что контуры неподвижны и ферромагнетиков поблизости нет.
С учётом явления самоиндукции ток, например в контуре 1, определяется по закону Ома:
1 1 = E1 − 1 1 − 12 2
где E1 сторонняя Э. Д. С. в контуре 1, 1 индуктивность контура 1.
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
6/34

Э. Д. С. взаимной индукции
Явление взаимной индукции заключается в возникновении Э. Д. С. индукции в одном из контуров при изменении тока в другом.
|
1 |
2 |
|
|
2 |
|
1 |
|
E1 = − |
|
= − 12 |
|
, |
E2 = − |
|
= − 21 |
|
|
|
|
|
|||||
Будем предполагать, что контуры неподвижны и ферромагнетиков поблизости нет.
С учётом явления самоиндукции ток, например в контуре 1, определяется по закону Ома:
1 1 = E1 − 1 1 − 12 2
где E1 сторонняя Э. Д. С. в контуре 1, 1 индуктивность контура 1.
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
6/34

Э. Д. С. взаимной индукции
Явление взаимной индукции заключается в возникновении Э. Д. С. индукции в одном из контуров при изменении тока в другом.
|
1 |
2 |
|
|
2 |
|
1 |
|
E1 = − |
|
= − 12 |
|
, |
E2 = − |
|
= − 21 |
|
|
|
|
|
|||||
Будем предполагать, что контуры неподвижны и ферромагнетиков поблизости нет.
С учётом явления самоиндукции ток, например в контуре 1, определяется по закону Ома:
1 1 = E1 − 1 1 − 12 2
где E1 сторонняя Э. Д. С. в контуре 1, 1 индуктивность контура 1.
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
6/34
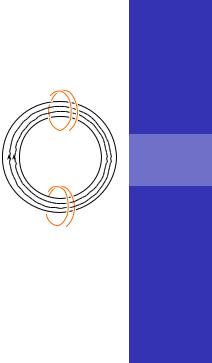
Взаимная индукция двух катушек на ферромагнитном торе
Найдём взаимную |
N1 |
индуктивность двух катушек, |
|
намотанных на тороидальный |
|
ферромагнитный сердечник. |
B |
|
Линии магнитной индукции лежат внутри сердечника
и возбуждаемое магнитное поле  от любой из обмоток будет иметь N2 всюду в сердечнике одинаковую по модулю напряжённость.
от любой из обмоток будет иметь N2 всюду в сердечнике одинаковую по модулю напряжённость.
Вспомним, что это справедливо, когда диаметр обмотки мал по сравнению с .
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
7/34
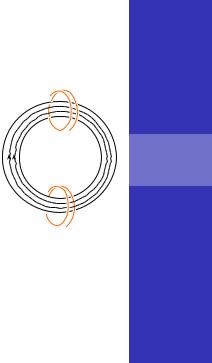
Взаимная индукция двух катушек на ферромагнитном торе
Найдём взаимную |
N1 |
индуктивность двух катушек, |
|
намотанных на тороидальный |
|
ферромагнитный сердечник. |
B |
|
Линии магнитной индукции лежат внутри сердечника
и возбуждаемое магнитное поле  от любой из обмоток будет иметь N2 всюду в сердечнике одинаковую по модулю напряжённость.
от любой из обмоток будет иметь N2 всюду в сердечнике одинаковую по модулю напряжённость.
Вспомним, что это справедливо, когда диаметр обмотки мал по сравнению с .
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
7/34
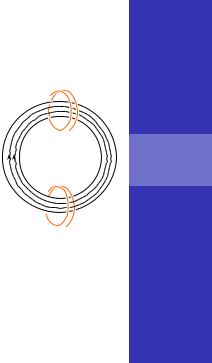
Взаимная индукция двух катушек на ферромагнитном торе
Найдём взаимную |
N1 |
индуктивность двух катушек, |
|
намотанных на тороидальный |
|
ферромагнитный сердечник. |
B |
|
Линии магнитной индукции лежат внутри сердечника
и возбуждаемое магнитное поле  от любой из обмоток будет иметь N2 всюду в сердечнике одинаковую по модулю напряжённость.
от любой из обмоток будет иметь N2 всюду в сердечнике одинаковую по модулю напряжённость.
Вспомним, что это справедливо, когда диаметр обмотки мал по сравнению с .
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
7/34

Если ток течёт только в обмотке 1, то |
N1 |
по теореме о циркуляции вектора :
1ℓ = 1 1
 B
B
где ℓ длина сердечника. |
|
Магнитный поток |
|
через сечение сердечника равен: |
N2 |
|
0 = 1 = 1 0 1 = 1 0 1 1
ℓ
Потокосцепление через вторую обмотку:
2 = 2 0 = 1 0 2 1 1
ℓ
Так как 2 = 21 1, то
21 = 1 0 1 2
ℓ
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
8/34

Если ток течёт только в обмотке 1, то |
N1 |
по теореме о циркуляции вектора :
1ℓ = 1 1
 B
B
где ℓ длина сердечника. |
|
Магнитный поток |
|
через сечение сердечника равен: |
N2 |
|
0 = 1 = 1 0 1 = 1 0 1 1
ℓ
Потокосцепление через вторую обмотку:
2 = 2 0 = 1 0 2 1 1
ℓ
Так как 2 = 21 1, то
21 = 1 0 1 2
ℓ
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
8/34

Если ток течёт только в обмотке 1, то |
N1 |
по теореме о циркуляции вектора :
1ℓ = 1 1
 B
B
где ℓ длина сердечника. |
|
Магнитный поток |
|
через сечение сердечника равен: |
N2 |
|
0 = 1 = 1 0 1 = 1 0 1 1
ℓ
Потокосцепление через вторую обмотку:
2 = 2 0 = 1 0 2 1 1
ℓ
Так как 2 = 21 1, то
21 = 1 0 1 2
ℓ
Уравнения
Максвелла
Взаимная
индукция
Понятие
взаимной
индукции
Коэффициенты
взаимной
индуктивности
Э. Д. С. взаимной индукции
Взаимная индукция двух катушек на ферромагнитном торе
Энергия магнитного поля
Уравнения
Максвелла
8/34
