
- •Формулы логики высказываний и логики предикатов
- •Равносильность в логике высказываний и влогике предикатов
- •Тавтологии
- •Понятие предиката. Кванторы
- •Нормальные формулы логики предикатов
- •Языки. Аксиомы. Правила вывода
- •Вывод. Вывод из гипотез
- •Теорема Дедукции. Следствия
- •Примеры выводимых формул
- •Непротиворечивость ив
- •Полнота ив
- •Правило суммы, произведения
- •Размещения и сочетания
- •Бином Ньютона
- •Разбиение. Полиномиальная теорема
- •Булевы функции
- •Формулы. Равносильность формул
- •Метод рекуррентных соотношений
- •Решение линейных рекуррентных соотношений
- •Понятие производящей функции
- •Интуитивное понятие алгоритма
- •Машины Тьюринга. Вычислимые функции
- •Рекурсивные функции
- •Алгоритмически неразрешимые проблемы
- •Нумерации машин Тьюринга
- •Критерии эффективности алгоритма
- •Полиномиальные и неполиномиальные алгоритмы
- •Основные понятия теории графов
- •Маршруты, цепи, циклы
- •Виды графов
- •Способы задания графов
- •Эйлеровы графы
- •Геометрическая реализация графов
- •Деревья. Лес.
- •Остовное дерево
- •Важнейшие числовые характеристики графов
- •Основные понятия теории кодирования
- •Критерий однозначности алфавитного кодирования
- •Алгоритм распознавания однозначности кодирования
- •Коды Хэмминга
- •Понятие множества
- •Операции над множествами. Свойства
- •Формулы включения и исключения.
-
Разбиение. Полиномиальная теорема
Пусть
дано множество X,
состоящее из n-
элементов. Рассмотрим разбиение мн-ва
X
на подмножества X1,X2,
… ,Xn
,такиe,
что 1.
 2
2 .
Число элементов в подмножествах
обозначим
соответственно через n1,n2,
… , nk.
Очевидно n1+n2,
… + nk=n.
Число таких разбиений мн-ва X
на подмножества X1,X2,
… ,Xк
обозначим через
.
Число элементов в подмножествах
обозначим
соответственно через n1,n2,
… , nk.
Очевидно n1+n2,
… + nk=n.
Число таких разбиений мн-ва X
на подмножества X1,X2,
… ,Xк
обозначим через
 (
( .
.
Лемма
4.9:
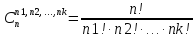 .
.
Д-во:
Каждое из подмножеств X1,X2,
… ,Xк
можно рассматривать как сочетание без
повторений. Поэтому 1-ое подмножество
X1
можно выбрать
 различными способами; 2-ое – X2
можно выбрать
различными способами; 2-ое – X2
можно выбрать
 ;
3-ое – X3
-
;
3-ое – X3
-

Тогда
по обобщенному правилу произведения
получаем(Усл обознач
 ):
):

Мультиполиномиальные коэффициенты
В
предыдущем параграфе была доказана
лемма
4.9
 .
.
Df
4.25 Числа
 называются мультипликативными
коэффициентами.
называются мультипликативными
коэффициентами.
Зам:
Мультипликативные коэффициенты
 стоят
при произвед-ии
стоят
при произвед-ии
 в разложении
в разложении
 .
.
Зам:
В
целом, верна так называемая полиномиальная
теорема. Ее суть выражается в след.
формуле:
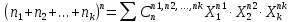 ,
где суммирование ведется по всем наборам
(n1,n2,
… ,nk)
таким, что:
,
где суммирование ведется по всем наборам
(n1,n2,
… ,nk)
таким, что:
-
n1+n2+…+nk=n
-
n1
 0;
n2
0;
n2 0;
…
nk
0;
…
nk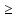 0
0
-
Булевы функции
Df.1.: Функция наз булевой, если она сама и ее аргументы принимают значение из мн-ва {0,1}
Замеч.: Булевы ф-ции наз еще истиностными или ф-циями алгебрв логики.
Замеч.: Булеву ф-цию f(x1,x2,... xn) можно задать так называемой таблицей истинности, в которой будет (n+1) столбцов и 2n – строк. В первых n-столбцах записывается все возможные наборы значений переменных x1,x2…xn, в (n+1)столбце записывается значение функции на этих наборах.
Прим.: Рассмотрим булеву ф-цию f(x1,x2), заданную следующей таблицей:
|
x1 |
x2 |
f(x1,x2) |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Условимся в таблицах наборы значений переменных x1,x2,... xn записывать в порядке возрастания чисел, определяемых этими наборами в двоичной записи. Такие табл будем наз стандартными.
Замеч.: Любые 2 стандартные таблицы двух различных ф-ций от одного и того же числа переменных отличаются только лишь последним столбцом, поэтому имеет место следующая теорема.
Теорема.1.:
Числа
всех различных булевых ф-ций от n
переменных =
 .
.
Замеч.:
По
аналогии с тем, что как определялись в
логике высказываний операции , здесь
определяется с такими же названиями
булевы ф-ции: ¯, ᴧ,ᴠ,→,↔. Кроме того,
введем в рассмотрение еще 3 новые булевы
ф-ции от 2-х переменных:

|
x1 |
x2 |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
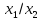 – штих Шеффера(отрицание
конюнкции)
– штих Шеффера(отрицание
конюнкции)
 – стрелка
Пирса(отрицание дизъюнкции)
– стрелка
Пирса(отрицание дизъюнкции)
 – сложение по mod
2 (отрицание эквивалентности).
– сложение по mod
2 (отрицание эквивалентности).
Df.2.:
Перемен
 – (
– ( )
в булевой ф-ции f
наз несущественной (или фиктивной), если
для для любого набора
)
в булевой ф-ции f
наз несущественной (или фиктивной), если
для для любого набора
 –
выпол-ся усл-е f(
–
выпол-ся усл-е f(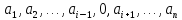 )
=
)
=
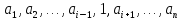 .
Иначе переменная наз существенной.
.
Иначе переменная наз существенной.
Прим.:
В
1-м прим. в булевой ф-ции f(x1,x2),,
заданной табл, переменная
 явл фиктивной.
явл фиктивной.
Замечание:
Если в булевой ф-ции
f(x1,x2,...
xn)
переменная xi
– явл фиктивной, то значит ф-ция а от
этой переменной не зависит и значит мы
имеем дело с некоторой ф-цией g(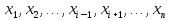 ).
В этом случае говорят, что ф-ция g
– получена из ф-ций f
путем удаления фиктивной переменной
xi,
а ф-ция f
получена путем введения фиктивной
переменной xi.
).
В этом случае говорят, что ф-ция g
– получена из ф-ций f
путем удаления фиктивной переменной
xi,
а ф-ция f
получена путем введения фиктивной
переменной xi.
Замеч.1.: В силу сделанного выше замечания каждую ф-цию, от n – переменных можно рассматривать как ф-цию от большого числа переменных.
Df.3.: 2-е булевых ф-ции наз равными, если одну из них можно получить путем введения или удаления фиктивных переменных.
Замеч.: Мн-во всех булевых ф-ций обозначим через P2.



