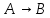- •Формулы логики высказываний и логики предикатов
- •Равносильность в логике высказываний и влогике предикатов
- •Тавтологии
- •Понятие предиката. Кванторы
- •Нормальные формулы логики предикатов
- •Языки. Аксиомы. Правила вывода
- •Вывод. Вывод из гипотез
- •Теорема Дедукции. Следствия
- •Примеры выводимых формул
- •Непротиворечивость ив
- •Полнота ив
- •Правило суммы, произведения
- •Размещения и сочетания
- •Бином Ньютона
- •Разбиение. Полиномиальная теорема
- •Булевы функции
- •Формулы. Равносильность формул
- •Метод рекуррентных соотношений
- •Решение линейных рекуррентных соотношений
- •Понятие производящей функции
- •Интуитивное понятие алгоритма
- •Машины Тьюринга. Вычислимые функции
- •Рекурсивные функции
- •Алгоритмически неразрешимые проблемы
- •Нумерации машин Тьюринга
- •Критерии эффективности алгоритма
- •Полиномиальные и неполиномиальные алгоритмы
- •Основные понятия теории графов
- •Маршруты, цепи, циклы
- •Виды графов
- •Способы задания графов
- •Эйлеровы графы
- •Геометрическая реализация графов
- •Деревья. Лес.
- •Остовное дерево
- •Важнейшие числовые характеристики графов
- •Основные понятия теории кодирования
- •Критерий однозначности алфавитного кодирования
- •Алгоритм распознавания однозначности кодирования
- •Коды Хэмминга
- •Понятие множества
- •Операции над множествами. Свойства
- •Формулы включения и исключения.
-
Формулы логики высказываний и логики предикатов
Df. 1.2: 1. Всякие символ, обозначающий высказывание является формулой.
2. Символы 1 и 0 являются формулами.
3. Если А – формула, То Ā – так же является формулой.
4. Если А и В – формулы, то следовательно выражения : (АᴧВ), (АᴠВ), (А→В),(А↔В) – так же являются формулами.
5. Формулами являются только те выражения, которые можно получить с помощью пунктов 1-4.
Зам.: В формулах, получаемых по определению 1.2, содержится слишком много скобок. Некоторые из них можно опустить, придерживаясь следующим соглашением об опускании скобок. Операции по силе своего действия располагаются в следующем порядке: ¯, ᴧ,ᴠ,→,↔. Исходя из этого, скобки опускаются таким образом, чтобы после их восстановления получить исходную формулу.
Df. 2.6:
-
Каждая формула логики высказываний является формулой(логики предикатов).
-
Каждый символ, обозначающий предикат, является формулой.
-
Если А – формула, то Ā
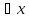 (A),
(A),
 (A)
- тоже являются формулами.
(A)
- тоже являются формулами. -
Если А и В – формулы, то след выражения тоже явл формулами:
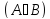 ,
,
 ,
,
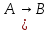 ),
),
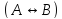 .
. -
Других формул нет.
Зам: Будем поддерживаться тех же правил об опускании скобок, что и ранее, учитывая только то, что кванторы связывают сильнее операции логики высказываний.
Df.
2.7:
В формулах
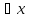 (А)
и
(А)
и
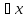 (A)
формула А наз. областью действия кванторов
всеобщности и существования соответственно.
(A)
формула А наз. областью действия кванторов
всеобщности и существования соответственно.
Df. 2.8: Вхождение переменной в формулу называется связным, если эта переменная следует за знаком квантора или находится в области действия от этой переменной.
Df. 2,9: Вхождение переменной, не являющейся связной, называется свободным.
Зам: Значение формулы зависит от переменных трех видов:
-
Логическая(обозначающие произвольные предикаты);
-
Предикатная(обозначающая произвольные предикаты);
-
Свободная.
Тогда, подставляя на места переменных их значения будем получать истинное значение формулы.
Df. 2.10: Формула А называется выполнимой на множестве М, если имеется хотя бы один набор значений переменных из М, на котором формула М принимает значение «1».
Df. 2.11: Формула называется выполнимой, если имеется множество, на котором она выполнима.
Df.
2.12:
Формула
называется тождественно истинной на
мн. М, если на
 наборе значений переменных из М она
принимает значение «истинна».
наборе значений переменных из М она
принимает значение «истинна».
Df.
2.13:
Формула называется логически общезначимой,
если она тождественно истина на
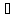 множестве.
множестве.
Зам:
Логически общезначимыми являются
тавтологии. Кроме того имеются логически
общезначимые формулы присущие только
логике предикатов. Например:
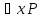 (х)→
(х)→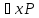 (х).
(х).
Df.
2.14:
Формула
называется логическим противоречием,
если она тождественно ложна на
 множестве.
множестве.
-
Равносильность в логике высказываний и влогике предикатов
Df.
1.3:
Пусть даны формулы А,В. Пусть
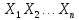 – совокупность букв, входящих хотя бы
в 1-ну из формул: А,В. Тогда формулы А и В
называются равносильными, если на
– совокупность букв, входящих хотя бы
в 1-ну из формул: А,В. Тогда формулы А и В
называются равносильными, если на
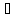 наборе значений
наборе значений
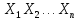 эти
формулы принимают одинаковые истинные
значения. В этом случае пишут А
эти
формулы принимают одинаковые истинные
значения. В этом случае пишут А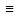 В.
В.
Зам: Как следует из определения для выяснения того, являются ли две формулы равносильными, надо сравнить значения этих формул на каждом наборе значении букв, входящих в эти формулы. Такое сравнение удобно проводить по таблице истинности.
Список основных равносильностей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зам: Пользуясь имеющимися равносильностями формулы можно преобразовывать к более простому или некоторому специальному виду.
Замечание: Отношения равносильности обладает след св-вами:
-
Рефлексивность:
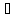 ф-лы А вып.
ф-лы А вып.

-
Симметричность:
 ф-л А,В вып. если
ф-л А,В вып. если
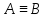 ,
то
,
то
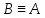
-
Транзитивность:
 ф-л А,В,С вып. если
ф-л А,В,С вып. если
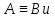
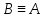 ,
то
,
то

Сл-но:
отношение равносильности является
отношением эквивалентности. Оно разбивает
мн-во всех ф-л на непересекающиеся классы
такие, что: 1.
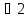 ф-лы из одного класса равносильны. 2.
Никакие 2 ф-лы из разных классов не явл.
равносильными.
ф-лы из одного класса равносильны. 2.
Никакие 2 ф-лы из разных классов не явл.
равносильными.
Df
2.15:
Формулы А и В называются равносильными
на мн. М, если на
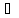 наборе значений переменных из М эти
формулы принимают истинные значения.
В этом случае пишут: А
наборе значений переменных из М эти
формулы принимают истинные значения.
В этом случае пишут: А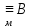 .
.
Df.2.16:
Формулы
А и В называются равносильными, если
они равносильны на любом множестве. В
этом случае пишут: : А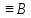 .
.
Зам: Равносильности логики высказываний остаются в силе и для логики предикатов. Кроме того имеются равносильности, присущие только логике предикатов.
23.

24,

25.
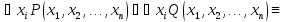
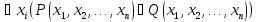
26.
 ᴠ
ᴠ
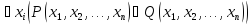
27.
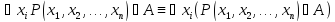 Где
А
Где
А
28.
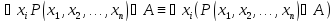 не
не
29.
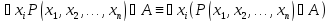 содержит
содержит
30.
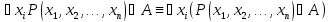 х
х
31.
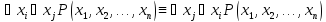
32.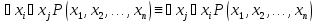
33.

34.
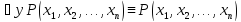
35.
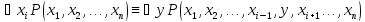
36.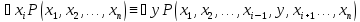
Зам: Пользуясь имеющимися равносильностями, формулы можно преобразовывать к более простому или к некоторому специальному виду.

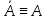
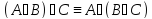
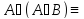 A
A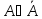
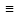 0
0

 A
A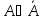
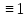
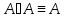
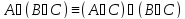
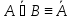
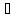
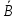
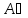 1
1
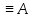
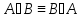
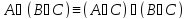

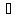
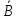
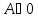
 0
0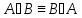
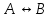
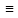
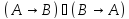
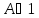


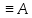
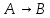

 B
B