7. Вывод. Вывод из гипотез

Df. 3.3: Выводом называется конечная последовательность формул, в которой каждая формула получена по 1-ой из схем аксиом или по правилу вывода из предсуществующих формул.

Df. 3.4: Формула называется выводимой, если имеется вывод, в котором эта формула находится на последнем месте. Если формула В выводима, то пишут ⱵВ.

Лемма 3.1: ⱵАА

Д-во: Запись ⱵАА, что выводима формула АА, т.е. имеется вывод, в котором на последнем месте находится формула АА. Поэтому для доказательства леммы нам надо построить вывод, в котором на последнем месте будет находиться формула АА. Построим этот вывод и запишем в столбик.

1. А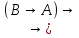А). По схеме аксиом 1.

2. (АА))) По схеме аксиом 2.

3. ( По МР из 1 и 2.

4. По схеме аксиом 1.

5. А. По МР из 4 и 3.

Таким образом мы построили вывод, в котором на последнем месте находится формула АА.Следовательно она выводима: ⱵАА. Чтд.

Df. Пусть дано некоторое(возможно пустое) множество формул Г. Формулы этого множества называются исходными или гипотезами. Тогда выводом формулы В из гипотез Г называется конечная последовательность формул, в которой на последнем месте находится формула В и в которой каждая формула является либо гипотезой, либо получена по 1-ой из схем аксиом, либо по правилу вывода из предыдущих формул. В этом случае пишут: Г Ⱶ В.

Зам: Если множество Г является пустым, то мы получаем просто вывод.

Зам: Если Г = {А₁А₂,…А_n} , то иногда вместо Г Ⱶ В пишут А₁А₂,…А_n Ⱶ В . Так в предыдущем примере можно написать, что А Ⱶ В . Отметим простейшее свойство вывода из гипотез:

1. Г, В Ⱶ В. Действительно в этом случае требуемым выводом из гипотез является вывод, состоящий из одной формулы В.

2. Если Г Ⱶ В, то Г, АⱵ В.

3. Если Г, А,С Ⱶ В, то Г, СА Ⱶ В.

8. Теорема Дедукции. Следствия

Теорема 3.1(ТД)

Если Г, А Ⱶ В, то Г Ⱶ А В

Следствие 1: 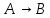, В Ⱶ.

Доказательство: Построим сначала вспомогательный вывод.

1. – гипотеза.

2. – гипотеза.

3. А – гипотеза.

4. В - по МР из 1 и 3.

5. С - по МР из 2 и 4.

Таким образом , , .

Применим к этому утверждению теорему дедукции: , В Ⱶ . Чтд.

Следствие 2: , В Ⱶ АС. Доказывается аналогично предыдущему.

9. Примеры выводимых формул

Лемма 3.2: Ⱶ.

Д-во: Построим требуемый вывод:

1. () ) - по схеме аксиом 3, где В:В, А:.

2. - по лемме 3.1

3. - по следствию 2 из 1 и 2.

4. ( - по схеме аксиом 1.

5. - по следствию 1 из 3 и 4.

Лемма 3.3: Ⱶ В

Лемма 3.4: Ⱶ.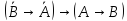

Лемма 3.5: Ⱶ

Лемма 3.6: Ⱶ

Лемма 3.7: Ⱶ

Лемма 3.8: Ⱶ ).

10. Непротиворечивость ив

Обычно аксиоматические теории строят так, чтобы они описывали какие-то «содержательные» математические теории (теорию натуральных чисел и т.д.). При этом аксиоматические теории желательно строить так, чтобы в соответствующих «содержательных» теориях не было противоречий, а их не будет в том случае, если аксиоматическая теория не противоречива.

Df 3.6: Аксиоматическая теория называется непротиворечивой, если в ней из каждой пары вида А и не выводимой является хотя бы одна.

Df 3.7: Формулам аксиоматической теории соответствуют утверждения соответствующей «содержательной» теории. Поэтому если аксиоматическая теория непротиворечива, т.е. из каждой пары формул вида А и 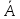не выводимой является хотя бы одна, то в соответствующей «содержательной» теории из каждой пары утверждений, одно из которых является отрицанием другого хотя бы одно место не имеет, а это и будет означать, что в «содержательной» теории нет противоречий.

Зам: Формулы исчисления высказываний можно рассматривать и как формулы логики высказываний, это значит символ интерплитировать как импликацию, а как отрицание. Будем считать, что формула ИВ является тавтологией, если она является тавтологией как формула ЛВ.

Лемма 3.9: Каждая выводимая формула является тавтологией.

Д-во: Пусть дана формула В и пусть выводом этой формулы является последовательность В₁В₂,…В_n, где В_n, где В_n, есть В. Индукцией от докажем, что В_i – тавтология.

1. Т.к. В₁ является 1-ой формулой вывода, то она может быть получена только лишь по одной из схем аксиом, тогда построив таблицу истинности для каждой из схем аксиом мы убедимся, что формулы, получаемые по схемам аксиом являются тавтологиями.

2. Пусть для всех i указаное выполняется. Покажем, что В_k - тавтология. Для формулы В_k возможны 2 случая:

1. В_k получена по одной из схем аксиом, тогда В_k – тавтология.

2. В_k получена по МР из В_m и В_n, где m,n. Т.к. m,n, то по индуктивному предположению В_m и В_n – являются тавтологиями. Кроме того, поскольку В_k получено по МР из В_m и В_n, то В_n= В_m В_k. Тогда, поскольку В_m и В_m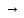 В_k являются тавтологиями, то по теореме 1.2 формула В_k тоже является тавтологией. Чтд.

Лемма 3.10: Рассматриваемое исчисление высказываний непротиворечиво.

Д-во: Рассмотрим произвольные пару формул вида В и . Возможны случая:

1. В – не выводима. Тогда по Df. ИВ – не противоречиво.

2. В – выводима. Тогда по лемме 3.9 В – является тавтологией. В этом случае тавтологией не является и поэтому не выводима. Чтд.