3. Тавтологии

Df. 1.4: Ф-ла наз. тавтологией, если она на наборе значений входящих в нее букв принимает значение «истина». Тавтологией наз. еще тождественно истинными ф-лами и законами логики.

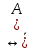
Прим: ; () B).

Теор 1.1: Ф-лы А и В равносильны , когда ф-ла явл тавтологией.

Д-во: Д-во теоремы следует из определения равносильности, эквивалентности, тавтологии.

Зам: Теорема 1.1 позволяет список равносильностей из предыдущего пункта преобразовать в список тавтологий. Для этого надо в каждой равносильности знак «» заменить на символ .

Теор 1.2: Если ф-лы А и явл тавтологиями, то и ф-ла В явл тавтологией.

Д-во: Пусть ф-лы А и явл тавтологиями. Предположим, что ф-ла В не является тавтологией. Это значит. Что найдется хотя бы 1 набор значений букв, входящий в ф-лу В, на котором ф-ла В принимает значение 0. Тогда на этом же наборе ф-ла принимает значение 0, поскольку А=1(как тавтология). Пришли к противоречию, поскольку ф-ла явл тавтологией, и значение 0 принимать не может. Сл-но наше предположение неверно, значит В – явл тавтологией. Чтд.

Теор 1.3 Пусть дана ф-ла А, в которую входит буква Х. Заменим в ф-ле А букву Х на букву Р и полученную ф-лу обозначим через В. Тогда, если ф-ла А являлась тавтологией, то и ф-ла В – так же явл тавтологией.

Прим: Пусть дана тавтология А=() . Заменим в этой ф-ле букву Х на ф-лу Р=У Z. Тогда по теореме 1.3 полученная ф-ла В=() тоже будет являться тавтологией.

Следств: Тавтологий имеется бесконечное множество.

Df. 1.5: Ф-ла наз тождественно ложной, если она на любом наборе значений, входящих в нее букв, принимает значение «ложь».

Зам: Ф-ла А явл тавтологией тогда и только тогда, когда ф-ла является тождественно ложной.

Df. 1.6: Ф-ла называется выполнимой, если имеется хотя бы один набор значений букв, входящий в эту ф-лу, на котором ф-ла принимает значение «истина».

4. Понятие предиката. Кванторы

4.1 Понятие предиката

Df.2.0. Под предикатом мы будем понимать повествовательное предложение с переменными, которое превращается в высказывание при подстановке на места переменных их значения.

Прим: Х+3=7 – не является повествовательным предложением.

Df. 2.1: Предикатом называется функция, аргументы которой принимают значения из некоторого множества М, а сама функция истинного значения {0;1}.

Зам: Предикаты будем обозначать большими буквами латинского алфавита, и в скобках будем указывать список аргументов. P(x), Q(x, y), S().

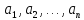Df. 2.2: Пусть дан предикат P(), определенный на множестве М. Тогда говорят, что набор значений () из множества М удовлетворяет(не удовлетворяет) предикату Р, если Р()=1 (Р()=0)

Df. 2.3: Пусть дан пред. P(), определенный на множестве М. Тогда Предикат Р называется:

1. Тождественно истинным, если любой набор () значений из М, удовлетворяет предикату Р.

2. Тождественно ложным, если никакой набор () значений из М, не удовлетворяет предикату Р.

3. Выполнимым, если имеется хотя бы 1 набор () значений из М, который удовлетворяет предикату Р.

Прим: Рассмотрим следующие предикаты на множестве Z:

1. P()= () – выполнимый. Тк, при условии, что =0, предикат становится ложным.

2. Q(x)=() – тождественно истинным.

3. S(x,y)=() – тождественно истинным.

Df. 2.4: Пусть даны предикаты P() и Q(), определены на одном и томже множестве М. Тогда: 1. Предикаты P и Q называются равносильными, если на любом наборе значений () из мн. М, они принимают одинаковые истинные значения. 2. Предикат Q является следствием предиката Р, если всякий набор значений () из мн. М, удовлетворяющий предикату Р, удовлетворяет и предикату Q.

Теор. 2.1: Пусть даны предикаты P() и Q(), определены на одном и том же множестве М. Тогда предикаты P и Q называются равносильными в том и только в том случае, когда каждый из них является следствием другого.

4.2 Кванторы

Df. 2.5: Пусть дан предикат P(), определенный на множестве М. Тогда:

1.Под выражением P() понимают высказывание, которое является истинным только в том случае, когда предикат P() является тождественно истинным на множестве М.

2.Под выражением понимают высказывание, которое является истинным только в том случае, когда предикат P() является выполнимым на множестве М.

Прим: Пусть даны предикаты P()=(x>3); Q(x)=(x²+1>0), определенные на множестве Z. Тогда 1. P()= (x>3)=0, P()=(x>3)=1. 2. Q()= (x²+1>0) = 1, Q()=(x²+1>0)=1.

Зам: Приписывание квантора слева к предикаты называется навешиванием квантора на предикат. Кванторы можно навешивать и на многоместный предикат. Пусть дан n-местный предикат P(), определенные на множестве М. Припишем к нему квантор x_m(1xn). В результате получим (n-1) местный предикат P() от Этот (n-1)-местный предикат на наборе принимает значение истинно только в том случае, когда одноместный предикат P() является тождественно истинным на множестве М.