
- •Формулы логики высказываний и логики предикатов
- •Равносильность в логике высказываний и влогике предикатов
- •Тавтологии
- •Понятие предиката. Кванторы
- •Нормальные формулы логики предикатов
- •Языки. Аксиомы. Правила вывода
- •Вывод. Вывод из гипотез
- •Теорема Дедукции. Следствия
- •Примеры выводимых формул
- •Непротиворечивость ив
- •Полнота ив
- •Правило суммы, произведения
- •Размещения и сочетания
- •Бином Ньютона
- •Разбиение. Полиномиальная теорема
- •Булевы функции
- •Формулы. Равносильность формул
- •Метод рекуррентных соотношений
- •Решение линейных рекуррентных соотношений
- •Понятие производящей функции
- •Интуитивное понятие алгоритма
- •Машины Тьюринга. Вычислимые функции
- •Рекурсивные функции
- •Алгоритмически неразрешимые проблемы
- •Нумерации машин Тьюринга
- •Критерии эффективности алгоритма
- •Полиномиальные и неполиномиальные алгоритмы
- •Основные понятия теории графов
- •Маршруты, цепи, циклы
- •Виды графов
- •Способы задания графов
- •Эйлеровы графы
- •Геометрическая реализация графов
- •Деревья. Лес.
- •Остовное дерево
- •Важнейшие числовые характеристики графов
- •Основные понятия теории кодирования
- •Критерий однозначности алфавитного кодирования
- •Алгоритм распознавания однозначности кодирования
- •Коды Хэмминга
- •Понятие множества
- •Операции над множествами. Свойства
- •Формулы включения и исключения.
-
Полнота ив
Здесь мы рассмотрим 3 вида полноты:
-
в широком смысле;
-
в узком смысле;
-
абсолютная.
Df. 3.7: ИВ называется полным в широком смысле, если в нем выводимы все тавтологии. Покажем, что рассматриваемое ИВ является полным в широком смысле.
Лемма
.3.11:
Пусть дана формула А и пусть В1В2,…Вn
–
совокупность всех символов 1-ой группы
алфавита, входящих в формулу А. Придадим
В1В2,…Вn
соответственно значения v1
,v2
, …, vn
и значение, которое при этом примет
формула А обозначим через V.
Тогда:
 Ⱶ
Ⱶ
 (1).
(1).
Лемма 3.12: Каждая тавтология является выводимой формулой.
Д-во:
Пусть формула А – тавтология и пусть
В1В2,…Вn
- совокупность символов одной группы
алфавита, входящих в формулу А. Тогда
по лемме
3.11
получаем
 Ⱶ
Ⱶ
 (2). Применим к (2) теорему дедукции:
(2). Применим к (2) теорему дедукции:
 (3) получаем:
(3) получаем:
А =
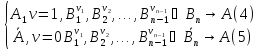 ;
;
Кроме
того, по Лемме3.6
будем иметь

Применим
к (4), (6) правила вывода МР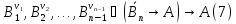 .
Наконец, применив к (5),(7) правила вывода
МР мы получим, что:
.
Наконец, применив к (5),(7) правила вывода
МР мы получим, что:
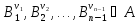 (8). Таким образом, имея (2), мы получим
(8). Тогда, применив еще (n-1)
описанную процедуру, мы получим
(8). Таким образом, имея (2), мы получим
(8). Тогда, применив еще (n-1)
описанную процедуру, мы получим
 Чтд.
Чтд.
Следств: Рассматриваемое ИВ является в широком смысле.
Df. 3.8: ИВ называется полным в узком смысле, если присоединив его схему аксиом любую не выводимую формулу, мы получаем противоречивую теорию.
Зам: Можно показать, что рассматриваемое выше ИВ является полным в узком смысле.
Df.
3.9:
ИВ называется абсолютно полным, если в
нем из каждой пары формул вида В и
 ,
выполнимой является хотя бы одна.
,
выполнимой является хотя бы одна.
-
Правило суммы, произведения
Основная задача комбинаторики: пересчет и перечисление элементов в конечных множествах.
Df. 4.18: Пересчет – это определение числа элементов данного конечного множества, обладающих каким-либо свойством или группой свойств.
Df. 4.19: Перечисление – это выделение всех элементов данного конечного множества, обладающих некоторым свойством или группой свойств.
Правило
суммы.
Правило Х1,
Х2,
…,Хк
–
попарно непересекающиеся мн-ва, т.е.
 .
.
Тогда
мощность

Зам:
Если
 ,
то
говорят, что х
,
то
говорят, что х Х
может быть выбран n-способами
Х
может быть выбран n-способами
Зам:
Если k=2,
то правило суммы для этого случая
формулируется след. образом: Если х Х
может быть выбран n-способами,
а объект y
Х
может быть выбран n-способами,
а объект y Y
может быть выбран m-способами,
то выбран либо х, либо у может быть
выполнен (m+n)
различными способами.
Y
может быть выбран m-способами,
то выбран либо х, либо у может быть
выполнен (m+n)
различными способами.
Правило произведения: Если объект х может быть выбран m-способами и после каждого и таких выборов объект у может быть выбран n различными способами, то выбор упорядоченной пары <x,y> может быть выполнен mn различными способами.
Д-во:
Пусть
объект ч выбирается из множества
{a1,a2,…,am}.
Через Хi
(1 i
i m)
обозначим множество упорядоченных пар,
в каждой из которых первым элементом
является ai.
m)
обозначим множество упорядоченных пар,
в каждой из которых первым элементом
является ai.
Очевидно,
множества Х1,
Х2,
…,Хm
– попарно не пересекаются и объединение
этих множеств дает нам искомое множество.
Кроме того,

Тогда
по правилу суммы получаем
 .
Чтд
.
Чтд
Зам: В общем случае правило произвед. формулируется след. образом: Пусть объект х1 может быть выбран m1-способами. Пусть после каждого из таких выборов объект х2 может быть выбран m2-разл. Спб-ми и т.д. Пусть после выбора х1,х2, … , хn-1 объект xn может быть выбран mn – различными способами. Тогда выбор упоряд последовательности <x1,x2, … , xn> может быть выполнен m1,m2, … , mn – различными способами.
