
- •Формулы логики высказываний и логики предикатов
- •Равносильность в логике высказываний и влогике предикатов
- •Тавтологии
- •Понятие предиката. Кванторы
- •Нормальные формулы логики предикатов
- •Языки. Аксиомы. Правила вывода
- •Вывод. Вывод из гипотез
- •Теорема Дедукции. Следствия
- •Примеры выводимых формул
- •Непротиворечивость ив
- •Полнота ив
- •Правило суммы, произведения
- •Размещения и сочетания
- •Бином Ньютона
- •Разбиение. Полиномиальная теорема
- •Булевы функции
- •Формулы. Равносильность формул
- •Метод рекуррентных соотношений
- •Решение линейных рекуррентных соотношений
- •Понятие производящей функции
- •Интуитивное понятие алгоритма
- •Машины Тьюринга. Вычислимые функции
- •Рекурсивные функции
- •Алгоритмически неразрешимые проблемы
- •Нумерации машин Тьюринга
- •Критерии эффективности алгоритма
- •Полиномиальные и неполиномиальные алгоритмы
- •Основные понятия теории графов
- •Маршруты, цепи, циклы
- •Виды графов
- •Способы задания графов
- •Эйлеровы графы
- •Геометрическая реализация графов
- •Деревья. Лес.
- •Остовное дерево
- •Важнейшие числовые характеристики графов
- •Основные понятия теории кодирования
- •Критерий однозначности алфавитного кодирования
- •Алгоритм распознавания однозначности кодирования
- •Коды Хэмминга
- •Понятие множества
- •Операции над множествами. Свойства
- •Формулы включения и исключения.
-
Понятие множества
Df. 4.1: Под множеством понимают набор объектов произвольной природы, которые называют элементами множества.
Зам: Множества будем обозначать большими буквами латинского алфавита, элементы множества малыми.
Df.
4.2: Говорят,
что любой элемент множества М принадлежит
М и пишут
 .
.
Зам:
Если множество А состоит из элементов
 ,
то пишут A={
,
то пишут A={ }
}
Df.
4.3: Множества,
не содержащие ни одного элемента,
называются пустыми и обозначаются
 .
.
Df.
4.4:
Универсальным множеством(универсалом)
называется множество, которому
 все элементы данного семейства множеств.
все элементы данного семейства множеств.
Df. 4.5: Два мн-ва А и В наз. равными, если они состоят из одних и тех же элементов (А=В).
Зам: Доказательство того, что два мн-ва А и В равны производится в два этапа:
-
Доказывается, что любой элемент множества А
 и
множеству В.
и
множеству В. -
Доказывается, что любой элемент множества В
 и
множеству А.
и
множеству А.
Df.4.6:
Говорят, что мн-во А является подмножеством
множества В, если любой элемент множества
А
 и множеству В.(А
и множеству В.(А
 В).
В).
Df.4.8:
Говорят, что мн-во А явл собственным
подмн-вом мн-ва В и пишут А
 В, если А
В, если А
 В, А
В, А
 В.
В.
Лемма 4.1: Пустое множество является подмножеством любого множества.
Д-во:
Предположим,
что нашлось такое множество А, что
 ,
это
значит имеется такой элемент x
,
это
значит имеется такой элемент x ,
что x
,
что x ;
но это противоречит тому, что
;
но это противоречит тому, что
 не содержит ни одного элемента. Чтд
не содержит ни одного элемента. Чтд
Df 4.8 Булеаном множества А называется семейство всех подмножеств множества А. Булеан множества А обозначается 2А.
Замечание: При задании множества порядок перечисления элементов множества роли не играет {a,b}={b,a}
Df 4.9 Мощностью конечного множества называется число элементов этого множества и обозначается |A|.
Лемма 4.2: Если |A|=n, то |2A|=2n
-
Операции над множествами. Свойства
Df
4.10
Объединением 2-ух множеств А и В называется
множество, обозначаемое А В,
которое состоит из тех и только тех
элементов, которые принадлежат хотя бы
одному из множеств А, В; т.е. А
В,
которое состоит из тех и только тех
элементов, которые принадлежат хотя бы
одному из множеств А, В; т.е. А B={x|x
B={x|x A
или x
A
или x B}.
B}.
Df.
4.11 Пересеч
2-ух мн-в А и В называется множество
А В={x|x
В={x|x A
A
 }
}
Df.
4.12 Два
множества А и В называются не
пересекающимися, если А В
=
В
= .
.
Df. 4.13 Пусть Е={E1,E2, … , Еn}- семейство подмн-в мн-ва А. Тогда Е наз. покрытием мн-ва А, если каждый элемент мн-ва А входит хотя бы в 1 подмножество Е1,Е2,…,Ек.
Df. 4.14 Покрытие Е множества А называется разбиением множества А, если каждый элемент исходного множества А входит ровно в одно подмножество семейства Е.
Df.
4.15 Разностью
двух множеств А и В называется множество
А\В, которое состоит из только из тех
элементов множества А, которые
 В,
т.е. А\В = {x|x
В,
т.е. А\В = {x|x A;х
A;х B}
B}
Df.
4.16 Симметричной
разностью множеств А и В называется
множество А B
(или А
B
(или А B),
которое состоит из тех элементов, которые
B),
которое состоит из тех элементов, которые
 ровно одному множеству, т.е. А
ровно одному множеству, т.е. А B={x|x
B={x|x A
и х
A
и х B
или x
B
или x B
х
B
х А}
А}
Df.
4.17 Дополнением
множества А называется множество,
обозначаемое
 ,
которое состоит из тех элементов, которые
,
которое состоит из тех элементов, которые
 А
А
 ={x|x
={x|x А
}
А
}
Лемма
4.3 А\В=А
Д-во:
-
Пусть x
 A\B.
Тогда по определению разности x
A\B.
Тогда по определению разности x A
A
 х
х B,
то x
B,
то x .
Таким образом, x
.
Таким образом, x A
и x
A
и x .
Следовательно x
.
Следовательно x A
A
-
Пусть x
 A
A .
Тогда, по определению операции пересечения
x
.
Тогда, по определению операции пересечения
x A
и x
A
и x Т.к.
x
Т.к.
x ,
то х
,
то х B.
Таким образом, x
B.
Таким образом, x A
и х
A
и х B.
Тогда по определению разности x
B.
Тогда по определению разности x A\B
Чтд
A\B
Чтд
Св-ва операций над мн-ми
Пусть множества А,В,С являются подмн-ми универсального мн-ва U. Тогда справедливы след. свойства:
10Идемпотентность,
т.е. А А=А
и A
А=А
и A A=A
A=A
20Коммутативность,
т.е. А B=
B
B=
B A
и A
A
и A B=
B
B=
B A
A
30
Ассоциативность,
т.е. А (B
(B С)=
(А
С)=
(А B)
B) С
, А
С
, А (B
(B С)=
(А
С)=
(А B)
B) С
С
40Дистрибутивность,
т.е. А (B
(B С)=(А
С)=(А B)
B) (А
(А С);
А
С);
А (B
(B С)=(А
С)=(А B)
B) (А
(А С)
С)
50Свойство
поглощения, т.е. . А (A
(A B)=A
; А
B)=A
; А (A
(A B)=A.
B)=A.
60Свойство
нуля, т.е. А =A;
А
=A;
А =A;
=A;

70Свойство
единицы, т.е. А ;
А
;
А ;
;
 =
=
80Свойство
де Моргана, т.е.
 =
=
 ;
;
 =
=
90Инволютивность,
т.е.
 =А
=А
100Свойство
дополнения, т.е. А ;
А
;
А
Докажем,
например, 2-ой закон дистрибутивности:
А (B
(B С)=(А
С)=(А B)
B) (А
(А С)
С)
Д-во:
-
Пусть x
 А
А (B
(B С).
Тогда по определению пересечения: х
С).
Тогда по определению пересечения: х А;
х
А;
х B
B C.
Т.к. х
C.
Т.к. х B
B C,
то х
C,
то х B
или х
B
или х С.
Следовательно: х
С.
Следовательно: х A
и х
A
и х B
или х
B
или х A
и х
A
и х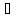 С.
Следовательно х
С.
Следовательно х (А
(А B)
B) (А
(А С)
С) -
Пусть х
 (А
(А B)
B) (А
(А С).
Тогда х
С).
Тогда х А
А B
или х
B
или х А
А С.
Откуда следует (х
С.
Откуда следует (х А
и х
А
и х B)
или (х
B)
или (х A
и х
A
и х С)
С)
 х
х A
и х
A
и х B
или х
B
или х C
C
 х
х A
и х
A
и х B
B C.
Тогда x
C.
Тогда x А
А (B
(B С)
С)
Чтд
