
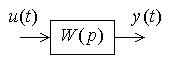
3. ВРЕМЕННЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ
Динамические свойства линейных звеньев и систем автоматического управления в целом (рис. 3.1) могут быть описаны уравнениями и графическими характеристиками. В теории автоматического управления применяются два типа таких характеристик – временные и частотные.
Рис. 3.1
Эти характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида.
Таким образом, временные и частотные характеристики однозначно связаны с уравнением звена и наряду с ним являются исчерпывающим описанием динамических свойств звена.
3.1. Временные характеристики
Переходная, или временная, характеристика (функция) звена представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным.
Переходная характеристика обозначается h(t). Единичное ступенчатое воздействие обозначается 1(t) и может быть описано следующим равенством:
0 при t 0,
1(t)
1 при t 0.
Таким образом, при u(t) 1(t) справедливо y(t) h(t).
54
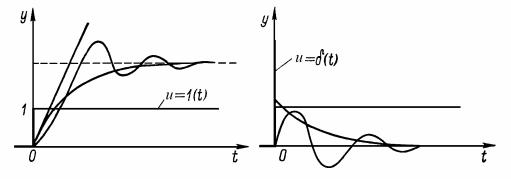
На рис. 3.2, а показаны три различных вида переходных характеристик, соответствующих различным типам звеньев.
а |
б |
Рис. 3.2. Переходные характеристики
Наряду с переходной характеристикой применяется импульсная переходная (временная) характеристика или функция, называемая еще весовой функцией (функцией веса). Эта характеристика представляет собой реакцию звена на единичный импульс. Единичный импульс (единичная импульсная функция, или дельтафункция) – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности.
Импульсная переходная характеристика обозначается w(t). Единичный импульс обозначается δ(t).
Математически дельта-функцию можно записать так:
|
при |
t 0, |
|
δ(t) |
0 |
при |
t 0. |
|
|||
При этом согласно определению
δ(t)dt 1.
Таким образом, при u(t) δ(t) получаем y(t) w(t).
На рис. 3.2, б единичный импульс условно показан в виде утолщения на оси ординат. Там же изображены и типичные формы самих импульсных переходных характеристик.
Дельта-функция просто связана с единичной ступенчатой функцией:
55

(t) d1(t). dt
Отсюда следует аналогичная связь между переходной и весовой функциями линейных звеньев:
w(t) |
dh(t) |
|
(3.1) |
|
dt |
||||
|
|
|||
и наоборот |
|
|||
|
t |
|
||
h(t) w(t)dt. |
(3.2) |
|||
0 |
|
|
||
Учитывая это простое соотношение |
между переходной |
|||
и весовой функциями, ниже будем применять главным образом первую из них. Вторую функцию при необходимости всегда можно получить из первой путем дифференцирования по (3.1).
Зная переходную или весовую функцию, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:
t |
du(τ) |
dτ, |
(3.3) |
|
y(t) h(t)u(0) h(t τ) |
||||
|
||||
0 |
dτ |
|
||
|
|
|
||
где u(0) – значение u(t) при t 0; |
|
|
|
|
t |
|
|
|
|
y(t) h(0)u(t) w(t τ)u(τ)dτ. |
(3.4) |
|||
0
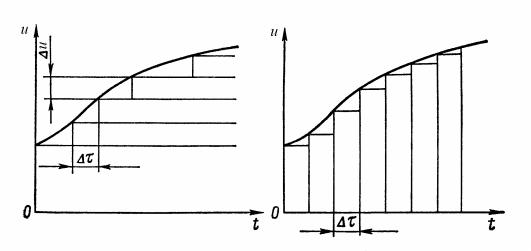
На рис. 3.3, а дана геометрическая интерпретация выражения (3.3). Реакция звена y(t) на произвольное воздействие u(t) определена как предел суммы реакций на ступенчатые воздействия высотой u u τ, на которые можно разложить u(t), при τ 0.
Выражение (3.4) для y(t) через весовую функцию w(t) геометрически интерпретируется на рис. 3.3, б как предел суммы реакций на импульсы шириной τ при τ 0. Его можно представить еще в таком виде:
t |
|
y(t) h(0)u(t) w(τ)u(t τ)dτ. |
(3.5) |
0
Выражения (3.3) и (3.4) легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки. Заметим, что первое слагаемое h(0)u(t) в (3.4) и (3.5) у реальных инерционных
56
звеньев равно нулю, так как реакция на их выходе всегда отстает от входного воздействия, т. е. h(0) 0. Поэтому в дальнейшем (3.4) и (3.5) приводятся без первого слагаемого.
а |
б |
Рис. 3.3. Геометрическая интерпретация выражения для реакции звена на произвольное воздействие
В выражениях (3.3), (3.4) и (3.5) в качестве верхнего предела интеграла вместо t может стоять , так как при τ t, т. e. при отрицательных значениях аргумента, функции h(t τ) и w(t τ) равны нулю.
Переходные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразования Лапласа.
Осуществим прямое преобразование Лапласа над уравнением звена, записанным в общем виде:
Q(p)y(t) R(p)u(t). |
(3.6) |
Считая начальные условия нулевыми и учитывая, что обе части |
|
этого уравнения представляют собой |
сумму производных |
с постоянными коэффициентами, получим: |
|
Q(p)Y(p) R(p)U(p). |
|
Здесь U(p) L[u(t)],Y(p) L[y(t)] – |
изображения Лапласа |
функций u(t) и y(t); Q(p) и R(p)– полиномы, отличающиеся от исходных полиномов Q(p) и R(p) уравнения (3.6) только заменой оператора дифференцирования p на комплексную переменную p c j .
57

Отсюда
Y(p) W(p)U(p), |
(3.7) |
где W(p) R(p) – передаточная функция звена.
Q(p)
В случае, когда входное воздействие u(t) представляет собой единичный импульс δ(t), учитывая, что его изображение по Лапласу L[δ(t)] 1, из (3.7) получаем следующее выражение для изображения весовой функции звена:
L[w(t)] W(p), |
(3.8) |
т. е. |
|
w(t) L 1[W(p)]. |
(3.9) |
Таким образом, весовая функция определяется через передаточную функцию по формуле обратного преобразования Лапласа, т. е. является ее оригиналом.
В случае когда u(t) 1(t), учитывая, что L[1(t)] 1/ p, из (3.7) получаем выражение для изображения переходной характеристики:
L[h(t)] W(p). p
Соответственно, переходная характеристика звена h(t) L 1 W(pp) .
Выражения (3.7) и (3.8) можно трактовать как определения передаточной функции. Согласно (3.7) передаточная функция определяется как отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях. Согласно (3.7) передаточная функция есть изображение Лапласа весовой функции.
Пример 3.1. Определить переходную и весовую функции звена с передаточной функцией
W(p) |
|
2(p 1) |
. |
|
|
|
|
|
|||
|
(0,5p 1)p |
|
|||
Решение. Передаточная функция W(p) является изображением |
|||||
Лапласа весовой функции w(t). |
Полюса |
передаточной функции |
|||
p1 0, p2 2 являются простыми, |
и весовую функцию w(t) можно |
||||
определить по формуле (2.16). |
В |
данном |
случае A(p) 2(p 1), |
||
58

B (p) p 1 и для весовой функции в соответствии с (2.16) получаем
|
|
|
|
w(t) |
2 |
e |
0 |
|
2 |
|
e |
2t |
2(1 e |
2t |
). |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как L{1(t)} 1/ p, |
то для изображения переходной функции |
|||||||||||||||||||||||||||||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2(p 1) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
H(p) W(p) |
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
(0,5p 1)p2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В этом случае полюс |
|
p1 0 |
|
имеет кратность |
|
n1 2, |
а полюс |
|||||||||||||||||||||||||||||||||
p2 2 |
– простой. |
Поэтому |
|
|
слагаемое, соответствующее |
полюсу |
||||||||||||||||||||||||||||||||||
p1 0, |
найдем по |
(2.15), |
|
а |
|
слагаемое, |
|
соответствующее |
полюсу |
|||||||||||||||||||||||||||||||
p2 2, – по (2.16). Согласно (2.15) имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
lim |
d |
[H(p)p2ept ] lim |
|
d |
[ |
2(p 1) |
ept] |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
p 0 dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
p 0 dp |
|
0,5p 1 |
|
|
|
|
|
||||||||||||||||||
|
lim[ |
2(0,5p 1) 2(p 1)0,5 |
e |
pt |
|
|
2(p 1) |
te |
pt |
] 1 2t. |
||||||||||||||||||||||||||||||
|
|
|
(0,5p 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
p 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5p 1 |
|
|
|
|
|
|||||||||||||||
Так как |
|
A(p) 2(p 1), |
|
|
|
|
|
(p) 1,5p |
2 |
2p, |
|
для |
слагаемого, |
|||||||||||||||||||||||||||
|
|
B |
|
|
||||||||||||||||||||||||||||||||||||
соответствующего полюсу p2 2, имеем (см. (2.16)) |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
e |
2t |
|
e |
2t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, переходная функция имеет вид |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h(t 1 2t e 2t. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Графики w(t) и h(t) показаны на рис 3.4. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Пример |
|
3.2. Пусть |
|
|
u(t) at, |
W(p) 1/(Tp 1) |
и при t 0 |
|||||||||||||||||||||||||||||||||
значение y(t) 0. Требуется определить y(t). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Решение. Сначала воспользуемся выражением |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
t |
|
y(t) h(t)u(0) h(t τ) |
|
0 |
Так как |
h(t) L 1{1/[(Tp 1)p]} |
преобразования |
Лапласа изображению |
оригинал (1 e αt)/α, то получим
t
h(t) 1 e T .
du(τ)dτ. dτ
и согласно таблице 1/[p(p α)] соответствует
59
Величина производной входного сигнала du(t)/dt a, тогда
t |
|
t τ |
|
t |
|
|
|
||||
y(t) (1 e |
|
T )adτ a[t T(1 e T )]. |
|||
0 |
|
|
|
|
|
Рис. 3.4
Этот же результат может быть получен также на основе таблицы преобразования Лапласа.
Преобразование Лапласа входного сигнала
U(p) L{at} a/ p2.
Тогда Y(p) a/[(Tp 1)p2].
Так как изображению 1/[p2(p α)] соответствует оригинал
(e αt αt 1)/α2, то получим
t
y(t) a[t T(1 e T )].
При этих преобразованиях α 1/T.
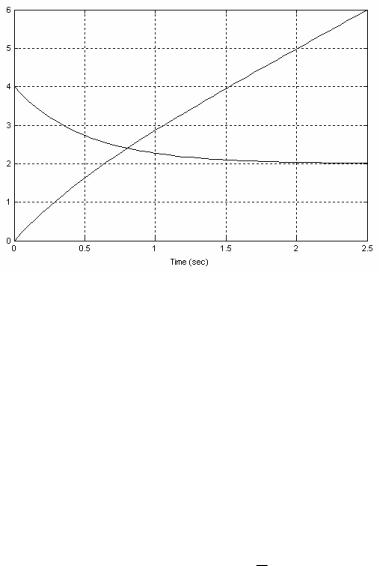
Графики u(t) и y(t) при a 1, T 0,5с показаны на рис. 3.5.
60
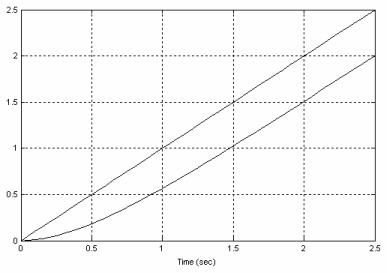
Рис. 3.5
3.2. Частотные характеристики
Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе. Пусть на вход звена (см. рис. 3.1) подано гармоническое воздействие
u umax sin t,
где umax – амплитуда, а ω – угловая частота этого воздействия.
По окончании переходного процесса на выходе звена будут существовать гармонические колебания с той же частотой, что и входные колебания, но отличающиеся в общем случае по амплитуде и фазе. В установившемся режиме выходная величина звена
y ymax sin (ωt ),
где ymax – амплитуда выходных установившихся колебаний; – фазовый сдвиг между входными и выходными колебаниями.
При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе звена зависят от частоты колебаний. Если постепенно увеличивать от нуля частоту колебаний и определять установившиеся значения амплитуды и фазы выходных колебаний для разных частот, можно получить
зависимость |
от частоты |
отношения |
амплитуд |
A(ω) уmax /umax |
и сдвига фаз |
(ω) |
выходных и |
входных |
установившихся |
|
|
|
|
61 |
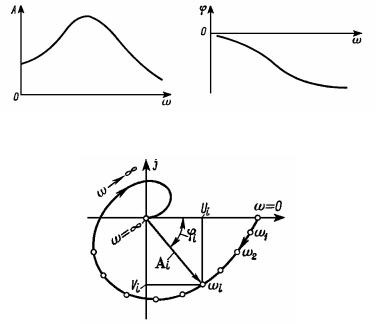
колебаний. Эти зависимости называются соответственно A(ω) – амплитудной частотной характеристикой (АЧХ) и (ω) – фазовой частотной характеристикой (ФЧХ). Примерный вид этих характеристик у обычных инерционных звеньев изображен на рис. 3.6, а и б.
Как показано на этих рисунках, у таких звеньев в силу их инерционности амплитудная частотная характеристика по мере увеличения частоты в конце концов спадает до нуля. При этом чем менее инерционно звено, тем длиннее его амплитудная частотная характеристика, т. е. тем больше полоса пропускаемых звеном частот, или, проще говоря, его полоса пропускания.
Теоретически частотная характеристика продолжается до бесконечности, но практически полоса пропускания оценивается значением частоты, при котором отношение амплитуд A(ω) уmax /umax окончательно становится меньше определенного, достаточно малого конечного значения. Это значение обычно берут равным 0,05 (на этой частоте амплитуда выходных колебаний падает до 5% амплитуды входных колебаний).
Наличие максимума у амплитудной частотной характеристики говорит о резонансных свойствах звена. Частота, соответствующая максимуму амплитудной характеристики, называется резонансной.
а б
в
Рис. 3.6. Частотные характеристики
62

Фазовая характеристика у обычных инерционных звеньев, как
показано на рис. 3.6, б, отрицательна |
( 0), т. |
е. выходные |
||
колебания отстают по фазе от входных, |
и это отставание растет |
|||
с частотой. |
|
|
|
|
Обыкновенные |
амплитудную |
и |
фазовую |
частотные |
характеристики можно объединить в одну характеристику – амплитудно-фазовую частотную характеристику (АФЧХ), используя A(ω)и (ω) в качестве полярных координат (рис. 3.6, в). Каждая точка амплитудно-фазовой частотной характеристики соответствует определенному значению частоты ω. Значения ω для конечного количества точек характеристики наносятся вдоль характеристики, как показано на рис. 3.6, в. Имея амплитудно-фазовую частотную характеристику, можно по этим точкам построить характеристики
A(ω)и (ω).
Амплитудно-фазовую частотную характеристику можно строить и в прямоугольной системе координат – в комплексной плоскости. При этом координатами будут показанные на рис. 3.6, в проекции
U(ω) |
и V(ω) вектора A(ω) на соответствующие оси. Зависимости |
U(ω) |
и V(ω) называются соответственно действительной |
(вещественной) и мнимой частотными характеристиками. Аналитические выражения для рассмотренных выше частотных
характеристик могут быть легко получены по передаточной функции. Если в выражение передаточной функции звена W(p)
подставить p jω, то получится комплексная величина W( jω), которая представляет собой функцию ω и является амплитуднофазовой частотной (или просто частотной) характеристикой звена. Ее модуль представляет собой амплитудную частотную характеристику A(ω), а аргумент – фазовую частотную характеристику (ω)
W(jω) W(p) p jω .
Докажем это. Для удобства воспользуемся символической формулой записи гармонических функций, т. е. представим установившиеся колебания на входе и выходе звена в виде
u(t) umaxejωt; |
|
(3.10) |
||
y(t) y |
|
|
|
|
max |
ej(ωt ). |
|
||
|
|
|
|
|
Уравнение звена в общем случае запишем так: |
|
|||
Q(p)y(t) R(p)u(t). |
(3.11) |
|||
|
|
|
|
63 |
