

11. ДИСКРЕТНЫЕ САУ
11.1. Понятие о дискретных САУ и их классификация
Сигналы, действующие в системах автоматического управления, бывают непрерывными и дискретными. Соответственно этому все САУ делятся на системы непрерывного действия и системы дискретного действия.
В системах непрерывного действия (в непрерывных системах) существуют только непрерывные сигналы, являющиеся непрерывными функциями времени (рис. 11.1, а). Все звенья этих САУ – звенья непрерывного действия, т. е. их входные и выходные величины представляют собой непрерывные сигналы.
а |
б |
в г
Рис. 11.1. Непрерывные и дискретные сигналы
САУ дискретного действия (дискретной САУ) называется система, в которой хотя бы одна величина представляет собой дискретный сигнал. Дискретный сигнал изменяется во времени дискретно, скачками (рис. 11.1, б, в, г). Существуют дискретные САУ, в которых имеются только дискретные сигналы. Такие системы
278
состоят полностью из звеньев дискретного действия, входные и выходные величины которых являются дискретными. Однако в большинстве дискретных систем имеются как дискретные, так и непрерывные сигналы. В состав таких систем наряду со звеньями непрерывного и дискретного действия входят звенья, преобразующие непрерывные сигналы в дискретные, и звенья, осуществляющие обратное преобразование.
Преобразование непрерывного сигнала в дискретный называется квантованием сигнала. Существуют два основных вида квантования: по уровню (рис. 11.1, б) и по времени (рис. 11.1, в). Сигнал, квантованный по уровню, может принимать только вполне определенные дискретные значения, соответствующие уровням, показанным на рис. 11.1, б горизонтальными линиями. Сигнал, квантованный по времени, изменяется скачком в фиксированные моменты времени, показанные на рис. 11.1, в вертикальными линиями.
На рис. 11.1, г изображен сигнал, квантованный и по уровню и по времени.
В соответствии с названными выше видами дискретных сигналов САУ дискретного действия делятся на три типа: релейные, импульсные и цифровые. Релейные САУ – это системы с квантованием по уровню, импульсные – с квантованием по времени, а цифровые – с применением обоих видов квантования.
11.2. Классификация и особенности динамики импульсных систем автоматического управления
11.2.1. Классификация импульсных систем автоматического управления. Импульсные системы – это системы, в которых действуют сигналы, квантованные по времени. Большинство замкнутых импульсных САУ можно представить, как показано на рис. 11.2. Здесь НЧ – непрерывная часть системы, а ИЭ – импульсный элемент. Импульсный элемент осуществляет квантование непрерывного сигнала X по времени, преобразуя его, таким образом, в дискретный сигнал Y.
279
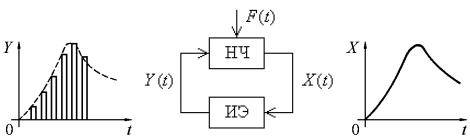
Рис. 11.2. Замкнутая импульсная система автоматического управления
На рис. 11.2 приведен возможный вид сигналов на входе и выходе импульсного элемента. Проходя непрерывную часть, дискретный сигнал сглаживается и превращается опять в непрерывный сигнал. Возможны и более сложные импульсные САУ, содержащие несколько импульсных элементов. Квантование, осуществляемое импульсным элементом в виде преобразования непрерывного сигнала в последовательность импульсов, называется импульсной модуляцией. Импульсная модуляция заключается в изменении одного из параметров выходных импульсов (модулируемого параметра) в функции величины входного сигнала (модулирующего сигнала). Модулируемым параметром для последовательности импульсов на выходе импульсного элемента может быть высота (амплитуда) импульса, его ширина и пауза между импульсами. Соответственно существуют три вида импульсной модуляции (рис. 11.3): амплитудно-импульсная модуляция (АИМ), широтно-импульсная модуляция (ШИМ) и время-импульсная модуляция (ВИМ). Последняя, в свою очередь, подразделяется на фазо-импульсную модуляцию (ФИМ) и частотно-импульсную модуляцию (ЧИМ). Во всех случаях форма импульсов в процессе модуляции принимается неизменной.
При АИМ (рис. 11.3, б) модулируемым параметром, зависящим от значения входного сигнала X (рис. 11.3. а) в начале очередного периода Tп повторения импульсов, является высота (амплитуда)
импульсов A .
Изображенный ранее на рис. 11.1, в квантованный по времени сигнал представляет собой тоже амплитудно-модулированный сигнал при ширине импульсов, равной периоду их повторения. При ШИМ (рис. 11.3. в) модулируемым параметром является ширина Tи
импульса, а при ФИМ (рис. 11.3. г) – запаздывание Tз импульса
280
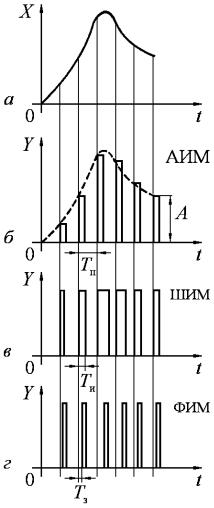
относительно начала периода. В случае ЧИМ (на рис. 11.3. не показана) модулируемым параметром, изменяющимся в функции величины X, является частота fп = 1/ Tп следования импульсов.
Рис. 11.3. Виды импульсной модуляции: а) – модулирующий сигнал; б) – амплитудно-импульсная модуляция; в) – широтно-импульсная; г) – фазо-импульсная
По виду модуляции импульсные САУ делятся соответственно на амплитудно-импульсные, широтно-импульсные и т. д. Основное распространение получили амплитудно-импульсные, затем широтноимпульсные системы. Поэтому в дальнейшем будем ориентироваться на них.
Импульсный элемент может входить в любую функциональную часть управляющего устройства или в объект управления.
Основные достоинства импульсных САУ обусловлены прерывистым характером передачи сигналов между отдельными
281
частями системы и состоят в возможности многоточечного управления, многократного использования линий связи, а также в повышенной помехозащищенности.
Первое достоинство заключается в том, что с помощью одного управляющего устройства импульсного действия можно управлять несколькими объектами путем циклического подключения этого управляющего устройства последовательно к каждому из объектов. Промежуток между двумя очередными импульсами, поступающими на один и тот же объект, используется для обмена дискретными сигналами с остальными объектами. В результате система управления всеми объектами в целом существенно упрощается по сравнению со случаем применения для каждого объекта отдельного управляющего устройства. Примером такой системы многоточечного управления является система регулирования температуры большого числа прессов горячей вулканизации с помощью одного регулятора. Каждый пресс снабжен термопарой, измеряющей температуру, и исполнительным реле, контакты которого включены в цепь питания электроподогревателя. С помощью шагового распределителя происходит «обегание» регулятором всех прессов, при подключении к каждому из которых регулятор либо включает, либо выключает нагрев в зависимости от величины температуры.
Возможность многократного использования одного канала связи для управления несколькими объектами, удаленными от места нахождения управляющих устройств импульсного действия, основана на том же принципе последовательного соединения объектов и соответствующих управляющих устройств линий связи с помощью синхронно действующих на обоих концах линии шаговых распределителей. Такое временное разделение каналов широко используется, в частности, для связи с летательными объектами и их управления.
Повышенная помехозащищенность импульсных систем обусловлена возможностью передавать информацию в виде очень коротких импульсов, в промежутке между которыми система оказывается разомкнутой и не реагирует на внешние возмущения.
В ряде случаев системы являются импульсными вне зависимости от указанных их достоинств – просто в связи с принципом действия отдельных частей системы. Сюда относятся
282
САУ, включающие радиолокаторы, высотомеры импульсного действия и т. п.
11.2.2. Особенности динамики импульсных систем автоматического управления. Импульсную САУ можно представить как систему непрерывного действия, в которой происходит периодическое прерывание контура, осуществляемое импульсным элементом. Обычно частота работы импульсного элемента выбирается значительно выше полосы пропускания непрерывной части системы, В этом случае импульсная САУ оказывается эквивалентной системе непрерывного действия, т.е. наличие квантования по времени не создает никакой принципиальной особенности в поведении системы. Это очевидно и из того, что в пределе при увеличении частоты повторения импульсов, т. е. при Tп → 0 , импульсная система превращается в систему непрерывного
действия.
Рис. 11.4. Переходной процесс в импульсной САУ с АИМ при большой частоте импульсов
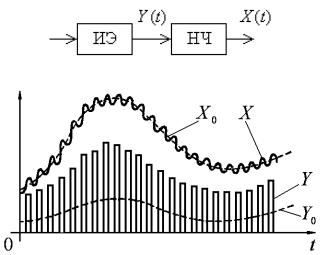
Непрерывная часть НЧ импульсной системы играет роль фильтра нижних частот. Она, как показано на рис. 11.4 для случая АИМ, реагирует только на низкочастотную составляющую Y0
импульсного сигнала Y на ее входе, несущую всю информацию о непрерывном сигнале на входе импульсного элемента ИЭ. Дискретность работы импульсного элемента вызывает лишь в качество побочного явления возникновение на выходе непрерывной
283
части системы высокочастотной составляющей в виде фона (см.
кривую |
X |
на рис. 11.4), частотный спектр которой кратен частоте |
работы импульсного элемента.
Таким образом, в данном случае происходит то же явление, что и релейных системах с вибрационной линеаризацией с помощью вынужденных колебаний. Эти системы, как видно из предыдущей главы, подобны импульсной системе с ШИМ.
Если частота |
п |
работы импульсного элемента недостаточно |
|
1/ T |
|
велика по сравнению с полосой пропускания непрерывной части системы, наличие этого элемента в системе существенно изменяет ее динамические свойства по сравнению с системой непрерывного действия, и, следовательно, при исследовании такой системы необходимо учитывать дискретный характер сигналов.
В отличие от релейных САУ импульсные системы могут быть как нелинейными, так и линейными. Линейной является импульсная система, у которой линейными уравнениями описываются как непрерывная часть, так и импульсный элемент.
11.3. Математическое описание импульсных систем автоматического управления
11.3.1. Описание линейных систем автоматического управления с АИМ. Математическое описание импульсной САУ (см. рис. 11.2) состоит из описания непрерывной части, методы которого нам уже известны, и описания импульсного элемента. Для описания последнего необходимо знать форму выходных импульсов, статическую характеристику элемента и его время запаздывания, если оно существенно. На рис. 11.3, иллюстрирующем работу импульсного элемента, время запаздывания для простоты принято равным нулю.
Статическая характеристика импульсного элемента – это зависимость модулируемого параметра от входного модулирующего сигнала. При описании импульсного элемента его статическая характеристика играет ту же роль, что и статические характеристики звеньев непрерывного действия при описании последних. В линейном приближении, т. е. для ограниченного диапазона изменения входного сигнала, статическая характеристика импульсного элемента может быть заменена прямой линией, и
284
соответственно вместо статической характеристики импульсный элемент будет характеризоваться коэффициентом передачи, определяемым наклоном этой характеристики в точке установившегося режима.
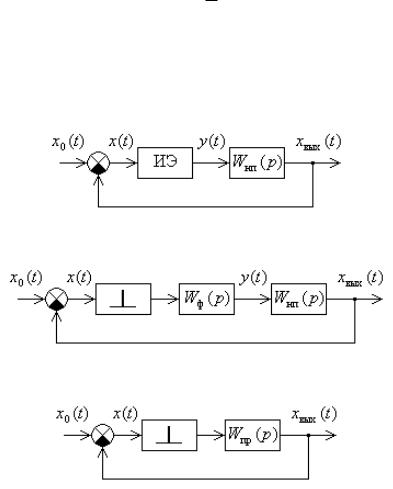
Начнем рассмотрение математического описания импульсных систем с линейной системы с АИМ. Такая система состоит из линейной непрерывной части, описываемой передаточной функцией
нп |
|
, и линейного импульсного элемента ИЭ с АИМ (рис. 11.5, а). |
W |
( p) |
|
Импульсный элемент в этом случае характеризуется формой импульсов, временем запаздывания и коэффициентом передачи
kи
=
a x
,
(11.1)
где x – величина сигнала на входе импульсного элемента в начале
очередного периода повторения импульсов Tп , а |
a |
– высота |
(амплитуда) выходного импульса в том же периоде. |
|
|
а
б
в
Рис. 11.5. К математическому описанию импульсной САУ с АИМ
Для описания такой системы после получения математического описания непрерывной части и импульсного элемента выполняем следующие три преобразования ее структурной схемы: разлагаем
285
реальный импульсный элемент на идеальный и формирующий элементы, переносим внешнее воздействие на вход импульсного элемента и заменяем действующие в системе реальные непрерывные сигналы на фиктивные дискретные сигналы.
Реальный импульсный элемент с выходными импульсами
произвольной |
формы |
можно представить, как показано на |
рис. 11.5, б, в |
виде |
последовательного соединения идеального |
импульсного элемента, выдающего на выходе идеальные мгновенные импульсы, и формирующего элемента (формирователя), преобразующего эти импульсы в импульсы, соответствующие
выходным |
импульсам реального импульсного элемента. На |
рис. 11.5, б |
дано условное изображение идеального импульсного |
элемента. Идеальными импульсами будем считать импульсы бесконечно малой ширины и бесконечно большой высоты, площадь которых, однако, конечна и численно равна входному сигналу в начале периода повторения. Иными словами, это δ -импульсы, но не единичной, переменной площади, которая является мерой входного сигнала в дискретные моменты времени. Эти идеальные импульсы условно показаны на рис. 11.5, б стрелками, длина которых соответствует величине площади импульса. В дальнейшем такой сигнал на выходе идеального импульсного элемента будем называть
идеальной импульсной функцией. |
|
Идеальный импульсный элемент называют |
δ -импульсным |
элементом или простейшим импульсным элементом. |
|
Передаточная функция формирующего элемента легко находится как изображение Лапласа от выражения для формы импульса на выходе реального импульсного элемента. Действительно, вспомним, что передаточная функция звена непрерывного действия представляет собой изображение Лапласа его весовой функции, т.е. реакции его на δ -импульс. Но поскольку на
входе формирующего элемента действуют именно |
δ -импульсы, |
следовательно, |
|
Wф ( p) = L[ yи (t)], |
(11.2) |
где
y |
и |
(t) |
|
|
– выражение для импульса единичной высоты на выходе
импульсного элемента.
Рассмотрим, например, импульсный элемент с выходными импульсами прямоугольной формы и ширины Tи . Такой импульс
286
можно представить в виде разности положительной и отрицательной единичных функций, сдвинутых на время Tи , т.е. здесь
yи (t) = kи [1(t) −1(t − Tи )] .
Отсюда, согласно (11.2),
ф |
( p) = k |
|
1 |
− |
и |
|
|||
W |
|
p |
||
|
|
|
|
1 |
e |
−T |
p |
= |
|
и |
|
||
|
|
|
|
|
p |
|
|
|
|
k |
|
(1 − e |
−T |
p |
) |
и |
и |
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
p |
|
|
|
.
(11.3)
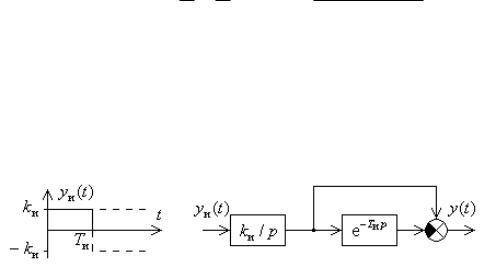
На рис. 11.6 показана соответствующая этой передаточной функции структурная схема формирующего элемента. Как видим, формирующий элемент представляет собой линейное звено непрерывного действия и может быть отнесен к непрерывной части системы.
Рис. 11.6. Структурная схема формирующего элемента при прямоугольной форме импульсов
Если в формуле (11.3) уменьшать длительность импульса |
Tи , |
сохраняя |
его |
площадь |
|
неизменной, |
т.е. |
одновременно |
||
пропорционально увеличивая |
|
и , то в пределе при |
и |
|
получим: |
|||
|
|
|
k |
|
|
T |
→ 0 |
|
Wф ( p) = kиTи , |
|
|
|
|
|
|
|
|
где величина
k |
и |
T |
|
и |
– площадь импульса на выходе импульсного
элемента, соответствующего входному сигналу, равному единице. Таким образом, в случае достаточно коротких импульсов
формирующий элемент может быть; представлен в виде идеального звена с коэффициентом передачи, равным отношению площади выходного импульса к величине входного сигнала. Практически это
допустимо, когда длительность импульсов |
и |
меньше основных |
|
T |
|
постоянных времени непрерывной части системы. В этом случае реакция системы на такой короткий импульс равна весовой функции и не зависит от ширины и реальной формы импульса, определяясь только его площадью.
При наличии в импульсном элементе запаздывания оно учитывается отдельным последовательным звеном запаздывания и
287
