
1.ОСНОВНЫЕ СВЕДЕНИЯ О НЕЛИНЕЙНЫХ САУ
1.1.Основные понятия и определения по нелинейным системам
Сточки зрения математического описания системы автоматического управления делятся на линейные и нелинейные. Нелинейная система – это система, содержащая хотя бы одно нелинейное звено, т. е. звено, описываемое нелинейным уравнением.
Все реальные САУ нелинейны, однако, часто имеется возможность, ограничившись рассмотрением малых отклонений от установившегося режима, свести задачу к исследованию линейной модели реальной системы путем линеаризации последней. Это возможно для систем, содержащих только несущественно нелинейные звенья.
Условия линеаризации звеньев определяют область применения теории линейных САУ. Кроме того, эта теория может быть использована для приближенного исследования САУ, содержащих и существенно нелинейные звенья, если эти нелинейности достаточно малы и ими в первом приближении можно пренебречь. Так, например, часто можно не учитывать имеющуюся у какого-либо звена зону нечувствительности, если она мала по сравнению с установившимися отклонениями в системе, определяемыми без ее учета. Также может быть отброшена петля гистерезиса (например, в статической характеристике электромашинного усилителя), если она достаточно узка. Примером существенной нелинейности, которой никогда нельзя пренебречь, является релейная характеристика. Включение в систему звена с такой характеристикой придает системе качественно новые свойства.
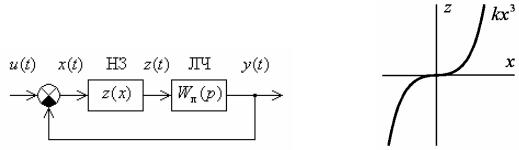
В результате математического описания нелинейной САУ составляется структурная схема, состоящая из линейных, т. е. линеаризованных, и существенно нелинейных звеньев (рис. 1.1, а). При описании последних, в свою очередь, осуществляется идеализация с целью упрощения этого описания вплоть до перехода в большинстве случаев к типовым нелинейностям.
8
а |
б |
Рис. 1.1. Нелинейная система автоматического управления: а – структурная схема; б – статическая характеристика нелинейного корректирующего звена
Нелинейности существенно усложняют исследование систем, так как нет общих методов решения описывающих их нелинейных дифференциальных уравнений. Однако в настоящее время имеется ряд методов решения отдельных классов нелинейных задач. Эти методы достаточно просты и позволяют путем их совместного применения успешно решать задачи анализа нелинейных САУ.
Хотя нелинейности затрудняют исследование САУ, их нельзя рассматривать как обязательно нежелательное явление. Нелинейности в равной степени могут оказывать как вредное, так и полезное влияние на работу системы. Более того, наряду с нелинейностями, присутствующими в САУ помимо нашего желания, например, в объекте управления, широко применяются нелинейности, специально вводимые в управляющее устройство системы с целью получения определенного положительного эффекта в работе САУ. К таким нелинейностям относятся, в частности, релейные управляющие устройства и нелинейные корректирующие звенья в системах непрерывного действия.
Например, с помощью введения нелинейной коррекции в чисто линейных САУ можно устранить известное противоречие между быстродействием и колебательностью, обеспечив возможность независимого выполнения требований по каждому из этих показателей. Если в линейной САУ для повышения быстродействия увеличивать коэффициент передачи разомкнутой системы то предел этому увеличению создает возрастающая в конце концов колебательность переходного процесса. Применение линейной коррекции позволяет повысить максимально достижимое при этом значение коэффициента передачи, однако принципиально не снимает
9
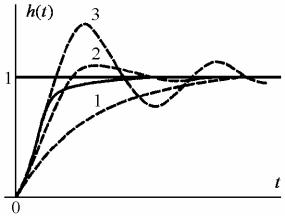
указанного противоречия, требующего компромиссного решения при выборе коэффициента передачи и самой коррекции. Сказанное иллюстрируется рис. 1.2, где приведены переходные характеристики 1, 2 и 3 линейной САУ при трех настройках коррекции, дающих все возрастающую форсировку процесса.
Рис. 1.2. Переходная характеристика системы при нелинейной коррекции
Указанное противоречие можно устранить, если изменять коррекцию в ходе входного процесса так, чтобы в первой его части коррекция определялась только по условию обеспечения требования к быстродействию, а затем изменялась, исходя из требования к устойчивости и колебательности процесса. При этом коррекция, выбранная для первой части переходного процесса, будет настолько сильной, что если ее не изменять к концу, переходный процесс получится с очень большой колебательностью вплоть до неустойчивости.
Такое изменение коррекции в ходе переходного процесса и означает переход к нелинейной коррекции, поскольку сводится к изменению структурной схемы или параметров корректирующих звеньев в функции переменных величин, характеризующих процессы в системе. При больших отклонениях от установившегося режима, соответствующих началу переходного процесса, коррекция должна обеспечивать максимально быстрое устранение этого отклонения, а затем, когда отклонение снижено до достаточно малой величины, необходима коррекция, обеспечивающая неколебательное окончание процесса.
10
Практически такая нелинейная коррекция реализуется либо с помощью реле, осуществляющих переключение корректирующих звеньев в функции выходной величины системы или какой-либо другой переменной, либо с помощью нелинейных звеньев со специально подобранными характеристиками, включенных последовательно с линейными корректирующими звеньями и изменяющих коэффициент передачи в ходе переходного процесса. Например, требуемая форсировка при больших отклонениях от установившегося состояния может быть получена включением последовательно в прямой канал или в каналы форсирующих корректирующих воздействий нелинейного звена с вогнутой характеристикой, подобной приведенной на рис. 1.1, б. Того же результата можно достигнуть введением нелинейного звена с выпуклой характеристикой типа характеристики с насыщением в цепь отрицательной обратной связи или в цепь корректирующих воздействий, демпфирующих переходный процесс.
В результате применения подобной нелинейной коррекции может быть получен процесс, изображенный на рис. 1.2 сплошной линией. Начальная часть процесса совпадает с переходной характеристикой 3 линейной системы, а далее происходит увеличение демпфирования и процесс переходит в монотонное окончание, близкое концу характеристики 1.
1.2. Особенности динамики нелинейных систем
Нелинейности придают САУ ряд качественно новых свойств, невозможных в линейных САУ. Нелинейные системы неизмеримо богаче по своим возможностям, чем линейные. Последние образуют, собственно говоря, довольно узкий класс систем, представляющих собой результат предельного упрощения реальных нелинейных систем.
У линейных систем точность, устойчивость и качество переходных процессов не зависят от величины внешних воздействий. Благодаря применимости к линейным системам принципа суперпозиции изменение величины внешнего воздействия вызывает в них только пропорциональное изменение абсолютного отклонения выходной величины, не сказываясь на качестве переходного процесса (его колебательности, длительности). Последнее иллюстрируется рис.
11
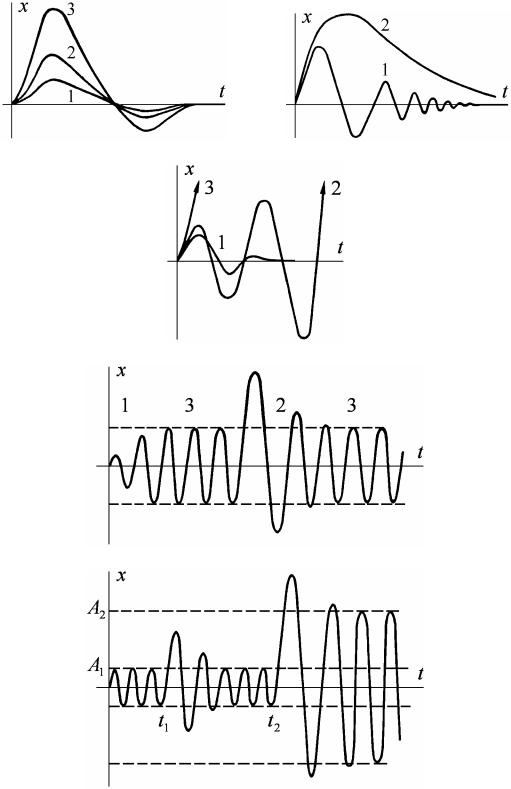
1.3, а, где приведены переходные характеристики для трех значений внешнего воздействия, пропорциональных числам, которыми отмечены характеристики.
а |
б |
в
г
д
Рис. 1.3
12
Устойчивость линейных САУ вообще не зависит от внешних воздействий и определяется параметрами самой системы. Если линейная система устойчива, то это значит, что она устойчива относительно любого установившегося режима и переходная составляющая любого процесса всегда будет сходящейся.
В нелинейных системах дело обстоит сложнее. Качество переходных процессов в них изменяется при изменении величины внешнего воздействия, например, как показано на рис. 1.3, б. При этом в отличие от линейных систем период колебаний процесса не постоянен, а изменяется по мере изменения отклонения. Чаще всего он уменьшается с уменьшением отклонения (рис. 1.3, б). Более того, нелинейная система, устойчивая при одних значениях внешних воздействий, может оказаться неустойчивой с возникновением расходящегося переходного процесса при других значениях этого воздействия. Это иллюстрируется рис. 1.3, в и г.
На рис. 1.3, в показан случай, когда система, устойчивая при малых воздействиях (кривая 1), неустойчива при больших воздействиях с получением колебательного (кривая 2) пли монотонного (кривая 3) расходящегося переходного процесса. На рис. 1.3, г представлен другой случай, когда, наоборот, при малых возмущениях переходный процесс является расходящимся (кривая 1), а при больших – затухающим (кривая 2). В этом случае, очевидно, установившимся режимом будут незатухающие колебания (кривые 3), После всякого воздействия, сбивающего эти колебания к нулю, в системе будет возникать расходящийся процесс их восстановлении, а после всякого воздействия, создающего большое отклонение, выходной величины, будет возникать процесс, сходящийся опять к этим колебаниям. Возможной причиной получения случая, показанного рис. 1.3, в, может быть, например, наличие насыщения в корректирующем звене, обеспечивающем устойчивость системы, а причиной второго случая, показанного на рис. 1.3, г, – наличие зоны нечувствительности у этого же звена.
Такие устойчивые собственные колебания с постоянной амплитудой, определяемой нелинейностями системы, называются автоколебаниями. Автоколебания представляют, собой новый вид установившегося режима, возможного при отсутствии внешних воздействий наряду со статическим установившимся режимом и характерного только для нелинейных систем. В линейных системах,
13
как мы знаем, собственные незатухающие колебания могут быть при нахождении системы на границе устойчивости, однако амплитуда этих колебаний определяется внешними воздействиями, будучи пропорциональна им. При этом такая линейная САУ является неработоспособной.
Если же в нелинейной САУ возможны автоколебания, то это еще не означает, что она непригодна к эксплуатации. Во-первых, эти автоколебания могут быть настолько малы по амплитуде, что не будут оказывать заметного влияния на работу системы. Это часто относится, например, к автоколебаниям, вызываемым наличием зоны нечувствительности. Во-вторых, может быть другой случай, когда в системе принципиально возможны автоколебания с большой амплитудой, однако, для того, чтобы они возникли, требуется соответственно очень большой внешний толчок. В результате может оказаться, что при всех практически возможных воздействиях на систему в ней могут быть только устойчивые переходные процессы. Этот случай соответствует кривым 1 и 2 на рис. 1.3, в, если предположить, что кривая 2 расходится не до бесконечности, а до автоколебаний с определенной амплитудой. Подобный случай может быть, например, если наряду с насыщением корректирующего звена, приводящим при больших воздействиях к нарушению устойчивости с переходом от кривой 1 к кривой 2, в системе имеется еще другое последовательное звено с насыщением на значительно большем уровне, которое и ограничивает амплитуду колебаний кривой 2.
Возможны нелинейные системы, в которых в зависимости от величины внешних воздействий возникают разные автоколебания, с разными амплитудами и частотами. Это иллюстрируется рис. 1.3, д. Здесь при малых воздействиях переходные процессы стягиваются к автоколебаниям с амплитудой A1, а при больших – к автоколебаниям
самплитудой A2 (моменты времени t1 и t2 – начала
соответствующих переходных процессов).
Описанные особенности устойчивости нелинейных систем требуют при рассмотрении устойчивости таких систем оговаривать начальные условия и внешние воздействия, как это делалось ранее при рассмотрении качества линейных систем. В результате, в случае нелинейных систем надо говорить не об устойчивости системы вообще, а об устойчивости определенного ее статического или динамического режима, т. е. определенного ее состояния или
14
движения при определенных отклонениях от него. В связи с этим при изучении нелинейных систем употребляются понятия устойчивости в малом, в большом и в целом.
Устойчивость в малом – это устойчивость при бесконечно малых отклонениях от исходного режима. Устойчивость в большом
– это устойчивость при конечных отклонениях, возможных в данной системе по условиям ее работы. Устойчивость в целом – это устойчивость при неограниченных отклонениях, т. е. при отсутствии каких-либо ограничений их. Нелинейная система может быть устойчива в малом, но неустойчива в большом (рис. 1.3, в). В линейных системах таких градаций устойчивости не существует, там система либо неустойчива, либо устойчива в целом. При этом в последнем случае будут устойчивы не только положения равновесия системы, но и любые вынужденные процессы.
При качественном рассмотрении процессов в нелинейных системах удобно использовать геометрическое представление, основанное на понятии фазового пространства.
1.3. Нелинейные звенья систем управления
Из рассмотрения приведенных ранее систем автоматического управления видно, что в них встречаются нелинейности самого различного вида. Будем характеризовать каждую нелинейность соответствующей функцией z z(x). При этом будем считать, что имеет место одномерная нелинейность, т. е. переменная z представляет собой функцию только одной переменной x. Возможны случаи и многомерных нелинейностей, когда переменная z – функция нескольких переменных, например z z(x, y). В дальнейшем будем рассматривать одномерные нелинейности, а некоторые многомерные нелинейности сведем к соединению одномерных.
Нелинейные звенья можно классифицировать по различным признакам: симметрии, гладкости, однозначности, непрерывности характеристик. Рассмотрим каждый из этих признаков.
Симметрия. Для нелинейных характеристик можно указать два
типа симметрии: |
|
1) если функция z(x) удовлетворяет условию |
|
z(x) z( x) |
(1.1) |
15
то такую характеристику называют симметричной относительно оси ординат или четно-симметричной, например, на рис. 1.4, е. При однозначной зависимости такие характеристики могут быть представлены рядом с четными степенями x:
|
2i , |
|
z(x) C2ix |
(1.2) |
|
i 0 |
|
|
где C – постоянный коэффициент; |
|
|
2) если функция z(x) удовлетворяет условию |
|
|
z(x) z( x), |
(1.3) |
|
то характеристику называют симметричной относительно начала координат или нечетно-симметричной, например, на рис. 1.4, е.. При однозначной зависимости z(x) такие характеристики могут быть представлены рядом с нечетными степенями х:
|
|
z(x) C2i 1x2i 1. |
(1.4) |
i 1 |
|
Характеристики, не удовлетворяющие ни одному из |
|
приведенных условий, называют несимметричными. |
|
В ряде случаев путем перемещения начала |
координат |
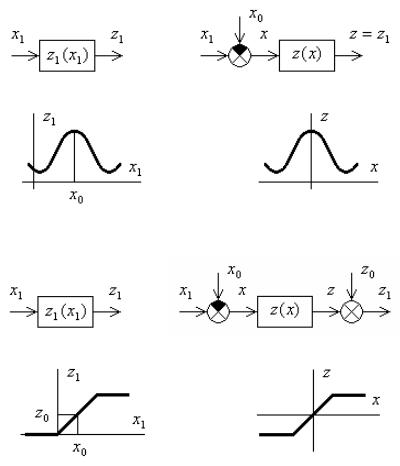
несимметричные характеристики могут быть приведены к симметричным. Перемещение начала координат соответствует введению дополнительных слагаемых на входе и выходе звена. Например, для несимметричной характеристики z1(x1) (рис. 1.4, а, б), можно ввести подстановку x1 x0 x так, чтобы полученная характеристика z(x) z1(x) оказалась симметричной относительно оси ординат. Такое преобразование координат соответствует введению сигнала x0 на входе звена и переходу от несимметричной характеристики z1(x1) к четно-симметричной z(x). (рис. 1.4, д, е).
Аналогично для характеристики z1(x1) (рис. 14.2, в, г) можно путем подстановки x1 x0 x и z1 x0 z получить нечетносимметричную характеристику z(x). Структурная схема и характеристика z(x), соответствующая данному преобразованию координат, показаны на рис. 1.4, ж, з.
16
а |
д |
б |
е |
в |
ж |
г |
з |
|
Рис. 1.4 |
Гладкость. Если в |
любой точке характеристики z(x) |
существует производная dz/dx, то характеристика относится к гладким, например, на рис. 1.4, е. Если на характеристике имеются изломы, в которых производная dz/dx имеет разрыв, то характеристика относится к ломаным, например, на рис. 1.4, е. Большую группу ломаных характеристик представляют кусочнолинейные характеристики, состоящие из отрезков прямых. В ряде случаев с целью облегчения расчета гладкие характеристики бывает удобно приближенно заменять кусочно-линейными ломаными.
Однозначность. Если каждому значению x соответствует одно определенное значение z, то характеристику называют однозначной. Если некоторому значению x соответствует несколько значений z в зависимости от режима, предшествовавшего рассматриваемому моменту, то характеристику называют многозначной. При этом число возможных значений z может лежать в пределах от 2 до ∞.
17
