
Характеристиками типа «люфт» обладают механические системы как с зазором, так и с сухим (кулоновым) трением. Рассмотрим простейшую модель механической системы с сухим трением. Здесь вращающий момент M уравновешивается моментом пружины αz (α – коэффициент пропорциональности) и моментом сухого трения xa , знак которого зависит от знака z.
В этой системе входным воздействием является вращающий момент x M , а выходной величиной – угол поворота вала z. Составляя уравнение моментов, получим
x M αz xa
или, обозначая k 1/α,
z k(x xa), |
(1.23) |
что соответствует графику, показанному на рис. 1.10, а, и уравнению
(1.22).
При этом:
dz/dx 0при |
x x |
xa. |
(1.24) |
Если в модели кроме момента пружины учесть момент вязкого трения βdz/dt или момент, обусловленный инерцией γd2z/dt2 (β и
γ– коэффициенты пропорциональности), то уравнение,
описывающее систему, принимает более сложный характер и модель не может быть сведена к звену типа «люфт». В этом случае влияние момента сухого трения должно быть выделено в виде нелинейного звена обратной связи, охватывающей линейное звено. Такая нелинейность будет рассмотрена дальше.
Звено типа «упор». В различных механических системах перемещение одной из частей механизма бывает ограничено в двух направлениях и при этом ведущая часть может неограниченно перемещаться.
Примером устройства, обладающего таким свойством, является механизм, у которого ведущий вал связан с ведомой частью с помощью фрикционной муфты, которая расцепляется как только момент сопротивления превышает некоторую предельную величину. Ведомая часть механизма имеет упоры с двух сторон, поэтому как только она доходит до упора и возникает большой момент сопротивления, фрикционная муфта расцепляется и ведущий вал начинает проворачиваться при неподвижной ведомой части. Однако как только направление вращения ведущего вала изменяется, муфта
28
снова входит в зацепление и ведомая часть механизма приходит в движение вместе с ведущим валом.
а |
б |
в
Рис. 1.11
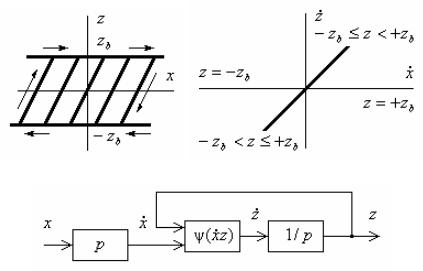
Если обозначить углы поворота ведущего и ведомого валов через x и z, то зависимость между ними выразится графиком, показанным на рис. 1.11, а. Каждому положению ведущего вала x в этом случае соответствует множество положений ведомого вала в пределах zb z zb.
Аналитически характеристика такого звена, называемого звеном типа упор, записывается так:
|
|
при x 0и zb z zb; |
|
||
kx |
|
|
|
|
|
|
|
при x 0и zb z zb; |
(1.25) |
||
z |
|
при x 0и z zb; |
|
||
|
|
|
|
||
|
0 |
|
|
|
|
|
при x 0и z z |
. |
|
||
|
|
|
b |
|
|
Зависимость z от x, выражаемая уравнением (1.25), показана на рис. 1.11, б. Структурная схема, соответствующая этому уравнению, изображена на рис. 1.11, в.
Нелинейные характеристики, соответствующие звену типа «упор», описывают процессы в системах с пневматическими и гидравлическими усилителями, а также электрическими двигателями рулевых машинок, имеющими концевые выключатели в цепи якоря.
29
Сравним нелинейные характеристики звеньев типа «люфт» и «упор». Для характеристик обоих типов всякое циклическое изменение x приводит к циклическому изменению z и на графике z(x) выражается некоторой замкнутой кривой. На рис. 1.10, а и 1.11, б также замкнутые кривые циклов показаны контурами абвг. Интересно обратить внимание на различное направление обхода по этим циклам. Для характеристики звена типа «люфт» направление обхода против часовой стрелки, а для звена типа «упор» – по часовой стрелке. Соответственно для характеристик типа «люфт», так же так и для характеристик типа «релейный гистерезис» (см. рис. 1.9),
 zdx 0,
zdx 0,
тогда как для характеристики типа «упор»:
 zdx 0.
zdx 0.
аб
в
Рис. 1.12
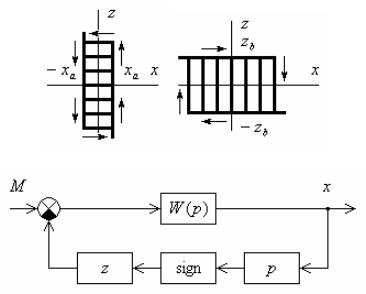
При стремлении коэффициентов усиления k в звеньях типа «люфт» и «упор» к бесконечности их характеристики становятся прямоугольными (рис. 1.12, а, б).
Примером характеристики типа «упор» с бесконечно большим коэффициентом усиления может служить влияние сухого (кулоновского) трения в системе механической передачи, если входным воздействием x считать поворот вала, а выходной величиной – момент трения z. В этом случае вращающий момент M
30

уравновешивается моментами пружины αx, вязкого трения βdx/dt,
сухого трения z(x) zb и инерции γd2z/dt2. При этом
z zbsignx
и
M z αx βdx/dt γd2x/dt2
Структурная схема, соответствующая последнему уравнению, имеет вид, изображенный на рис. 1.12, в.
Здесь:
W(p) |
1 |
|
α βp γp2 . |
(1.26) |
Цепь обратной связи, описываемая нелинейным звеном z(x), имеет характеристику, изображенную на рис. 14.10, б, и соответствует последовательному соединению дифференцирующего звена и нелинейности типа sign.
Звено типа «магнитный гистерезис». При рассмотрении устройств магнитной памяти большое распространение получили нелинейные характеристики, в которых гистерезисные петли представлены в виде кусочно-линейных замкнутых кривых. Пример характеристики звена типа «магнитный гистерезис» показан на рис. 1.13, а. Здесь характеристика может быть описана следующими уравнениями:
z μ1(x xa); |
(1.27) |
|
z μ2x C, |
|
|
|
|
|
где zb C zb, а μ1 и μ2 – постоянные коэффициенты.
а б
Рис. 1.13
31
При 1 и 2 0 гистерезисная петля имеет прямоугольную форму (рис. 1.13, б). Эта характеристика отличается от характеристики типа «люфт» при k (см. рис. 1.12, а) ограничением величины z, которая может лежать только в пределах от zb до zb.
1.5.Контрольные вопросы
1.Какая система называется нелинейной?
2.Какие бывают виды устойчивости?
3.Что такое автоколебания, когда они возникают?
4.По каким признакам можно классифицировать нелинейные
звенья?
5.Что такое многозначная характеристика?
6.Что такое «зона нечувствительности»?
7.Какое звено называют «ограничение или насыщение»?
8.Опишите звено «двухпозиционное реле с гистерезисом».
9.Опишите звено «трехпозиционное реле без гистерезиса».
10.Какие процессы описывают нелинейные характеристики, соответствующие звену типа «люфт»?
11.Какие процессы описывают нелинейные характеристики, соответствующие звену типа «упор»?
12.Расскажите про звено «магнитный гистерезис»?
32
