
11. СПОСОБЫ УЛУЧШЕНИЯ КАЧЕСТВА ЛИНЕЙНЫХ САУ
Проблема обеспечения требуемых свойств линейных автоматических систем является весьма сложной. В ней могут быть выделены прежде всего следующие частные задачи: обеспечение устойчивости (стабилизация); повышение запаса устойчивости (демпфирование); повышение точности регулирования в установившихся режимах (уменьшение или устранение статической ошибки воспроизведения задающего воздействия, уменьшение или устранение влияния постоянных возмущений); улучшение переходных процессов (увеличение быстродействия, максимальное уменьшение динамических ошибок воспроизведения воздействия и от возмущений).
Иногда несколько частных задач могут быть решены совместно, в других случаях они оказываются противоречивыми. В зависимости от назначения системы и предъявляемых к ней требований одни задачи становятся основными, а другие отодвигаются на второй план или снимаются.
Всякая система автоматического регулирования должна быть
устойчивой. Однако |
запас |
устойчивости |
в |
системе |
стабилизации |
|
(с постоянным |
или |
редко |
изменяемым |
задающим |
воздействием) |
|
может быть |
значительно |
меньше, чем |
в следящей системе |
|||
(с непрерывно или часто изменяющимся задающим воздействием). Если параметры регулируемого объекта определены приближенно или могут изменяться в процессе эксплуатации системы, то необходим больший запас устойчивости, чем при точно установленных и неизменных параметрах.
В системах стабилизации обеспечивается максимально возможное или хотя бы необходимое уменьшение влияния возмущений. В следящих системах, кроме того, обеспечивается
максимально |
возможное или |
необходимое быстродействие |
и уменьшение |
как статических, |
так и динамических ошибок |
воспроизведения задающего воздействия.
239
11.1. Коррекция динамических характеристик САУ
Обеспечение заданного качества систем автоматического управления достигается рациональным выбором структуры и параметров системы, а также введением в нее специальных устройств, называемых корректирующими. Корректирующие
устройства |
представляют |
собой |
динамические |
звенья |
|
с определенными |
передаточными функциями. При включении |
||||
в систему |
они |
производят |
такое |
перераспределение |
корней |
характеристического уравнения (нулей и полюсов передаточных функций разомкнутой и замкнутой систем), при котором САУ удовлетворяет не только критерию устойчивости, но и критериям качества переходных процессов.
11.1.1. Способы включения корректирующих устройств.
Коррекция динамических свойств САУ используется для выполнения требований по устойчивости, точности и качеству переходных процессов.
С точки зрения требований к точности САУ в установившихся режимах коррекция динамических свойств САУ может понадобиться для увеличения коэффициента передачи или порядка астатизма при сохранении устойчивости и определенного качества переходных процессов.
Коррекция применяется также как средство обеспечения устойчивости неустойчивой САУ, расширения области устойчивости, повышения качественных показателей переходных процессов.
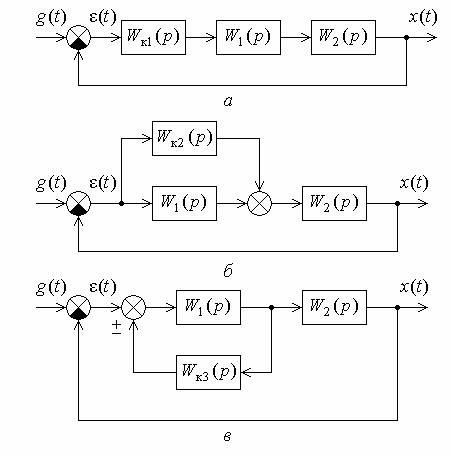
Осуществляется коррекция с помощью введения в систему корректирующих устройств с определенной, заранее подобранной передаточной функцией. Корректирующие устройства могут включаться последовательно (рис. 11.1, а) или параллельно: согласно параллельно (рис. 11.1, б) и встречно параллельно (рис. 11.1, в) с основными звеньями САУ. Последний тип коррекции называется также коррекцией с помощью корректирующих обратных связей.
Последовательное корректирующее устройство Wк1(p) включают непосредственно после датчика рассогласования или же после предварительного усилителя (рис. 11.1, а). Это связано с тем, что уровень сигнала рассогласования обычно весьма мал и корректирующее устройство снижает чаще всего уровень сигнала.
240
Применение последовательных корректирующих устройств наиболее удобно в системах, у которых сигнал управления представляет собой напряжение постоянного тока.
Рис. 11.1. Схемы включения корректирующих устройств в САУ
Применяют и второй вариант включения корректирующего устройства Wк2(p) в систему – параллельно одному из участков ее прямой цепи (рис. 11.1, б). Такое параллельное корректирующее устройство оказывается весьма удобным – при меньшей сложности обеспечивает нужное преобразование сигнала управления.
Другое, широко распространенное включение корректирующего устройства показано на рис. 11.1, в. В данном случае корректирующее устройство Wк3(p) является обратной связью, чаще всего отрицательной, которая охватывает один из элементов прямой цепи системы. Этим элементом обычно является исполнительный элемент или выходной каскад усилителя.
В линейных системах для корректирующего устройства одного типа всегда можно подобрать эквивалентное устройство другого
241
типа. Переход от одного типа устройства к эквивалентному другому типу производится при помощи формул перехода, которые получаются приравниванием передаточных функций разомкнутых цепей.
По каждой из структурных схем (рис. 11.1) составим выражение передаточной функции разомкнутой цепи и приравняем эти выражения друг другу. Получаем
Wк1(p)W1(p) Wк2 |
(p) W1 |
(p) |
W1 |
(p) |
. (11.1) |
|
1 W1(p)Wк3(p) |
||||||
|
|
|
|
|||
Из (11.1) определяют формулы перехода от одного вида корректирующего устройства к другому:
W |
(p) |
Wк2(p) W1(p) |
|
1 |
; |
|
|
|
|
||||
к1 |
|
W1(p) |
1 W1(p)Wк3(p) |
|
||
|
|
|
||||
|
|
|
|
|
|
W2 |
(p)W |
(p) |
|||
W |
(p) W (p)[W |
(p) 1] |
1 |
к3 |
|
; |
|
||||
|
|
|
|||||||||
к2 |
|
1 |
к1 |
|
|
1 W1(p)Wк3(p) |
|||||
|
|
|
|
|
|
||||||
Wк3(p) |
1 Wк1 |
(p) |
|
|
Wк2(p) |
|
|
. |
|||
Wк1(p)W1(p) |
|
|
|
|
|||||||
|
|
|
[Wк2(p) W1(p)]W1(p) |
||||||||
При отрицательном значении передаточной функции Wк2(p) выходной сигнал этого устройства должен вычитаться из выходного сигнала участка W1(p). Если значение передаточной функции Wк3(p) оказывается отрицательным, то это устройство должно включаться
ввиде положительной обратной связи.
Внастоящее время корректирующие устройства являются основным способом повышения качества линейных непрерывных систем управления по отклонению.
11.1.2.Последовательные корректирующие звенья.
Корректирующие звенья последовательного типа применяются в САУ с электрическим сигналом в виде напряжения постоянного тока u(t), который функционально связан с ошибкой ε(t) g(t) x(t) системы u(t) f[ε(t)], например u(t) kε(t). Этот сигнал подается на вход таких корректирующих звеньев.
Корректирующие звенья в большинстве случаев представляют собой типовые динамические звенья, основное назначение которых изменять свойства САУ в нужном направлении, и реализуются на пассивных или активных RLC-элементах.
242
Широкое применение получили следующие последовательные корректирующие звенья: пропорционально-дифференцирующее (ПД), пропорционально-интегрирующее (ПИ), пропорционально- интегро-дифференцирующее (ПИД).
Пропорционально-дифференцирующее звено. Идеальное ПД-
звено имеет следующую передаточную функцию
Wпд(p) kп kд p kп(1 Tд p), |
(11.2) |
где Tд kд /kп.
Выходная величина звена содержит две составляющие: пропорциональную входной величине и пропорциональную ее первой производной. Введение воздействия по производной изменяет значение коэффициента при p в первой степени в характеристическом полиноме D(p) замкнутой САУ. Это изменяет условия устойчивости и качество переходных процессов в САУ. Например, применение ПД-звеньев позволяет сделать структурно неустойчивые САУ структурно устойчивыми, т. е. обеспечивает устойчивость САУ с астатизмом выше первого порядка. Также можно сделать устойчивой САУ, структурно неустойчивую из-за наличия в ней неустойчивых звеньев.
ПД-звено является фильтром верхних частот, так как ЛАХ растет с увеличением частоты, расширяет полосу пропускания САУ, т. е. повышает ее быстродействие. ФЧХ ПД-звена положительна, звено уменьшает суммарное запаздывание по фазе в САУ.
Положительное воздействие по производной (kд 0) форсирует течение переходного процесса, отрицательное воздействие (kд 0)
замедляет течение переходного процесса.
Реальное ПД-звено обычно обладает инерционностью, его передаточная функция
W |
(p) |
kп kд p |
k |
|
1 Tд p |
, |
(11.3) |
|
|
||||||
пд |
|
T p 1 |
п 1 T p |
|
|||
|
|
пд |
|
пд |
|
||
где Tд kд /kп, Tпд Tд, kп kд /Tд.
Пропорционально-интегрирующее звено. Идеальное ПИ-
звено имеет передаточную функцию
W |
(p) |
kи |
k |
п |
|
kи |
(1 T p); |
(11.4) |
|
p |
|||||||
пи |
|
p |
|
и |
|
|||
243
реальное ПИ-звено –
W (p) |
1 |
|
kи kп p |
|
kи |
|
1 Tи p |
, |
(11.5) |
|
|
|
|
||||||
пи |
p Tпи p 1 |
|
p 1 Tпи p |
|
|||||
|
|
|
|||||||
где Tи kп /kи.
Таким образом, ПИ-звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена.
Частотные свойства ПИ-звена, как фильтра нижних частот, обратны таковым у ПД-звена.
ПИ-звено обычно применяют для повышения порядка астатизма при сохранении устойчивости и необходимого качества переходных процессов. При этом знак для воздействия по интегралу должен быть положительным; знак воздействия по производной может быть любым.
Пропорционально-интегро-дифференцирующее звено. Иде-
альное ПИД-звено имеет передаточную функцию
W |
(p) |
kи |
k |
п |
k |
д |
p |
kи |
(1 T p T T p2); |
(11.6) |
||||||
p |
p |
|||||||||||||||
пид |
|
|
|
|
|
|
|
и |
и д |
|
||||||
реальное ПИД-звено – |
|
|
|
|
|
|
|
1 Tи p TиTд p2 |
|
|
|
|||||
|
W |
(p) |
kи |
|
|
|
, |
(11.7) |
||||||||
|
|
|
|
|
|
|
||||||||||
|
пид |
|
|
|
p |
|
|
|
Tпид p 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где Tи kп /kи; Tд kд /kп.
ПИД-звено эквивалентно последовательному соединению либо интегрирующего звена и ПД-звена с воздействием по двум производным, либо ПИ-звена и ПД-звена с одной производной.
Частотные характеристики этого звена получаются сложением характеристик ПИ и ПД звеньев. Соответственно такое звено подчеркивает как нижние, так и верхние частоты, подавляя средние.
ПИД-звено повышает порядок астатизма (как и ПИ-звено) и дает более сильную коррекцию динамических свойств САУ.
Часто интегро-дифференцирующими звеньями называют не только звенья с передаточной функцией (11.7), но и другие звенья, АЧХ которых имеет минимум на средних частотах и растет в сторону как низких, так и высоких частот. Такую характеристику имеет, например, звено с передаточной функцией
W(p) |
k(T1p 1)(T2 p 1) |
. |
(11.8) |
|
|||
|
(T3p 1)(T4 p 1) |
|
|
244
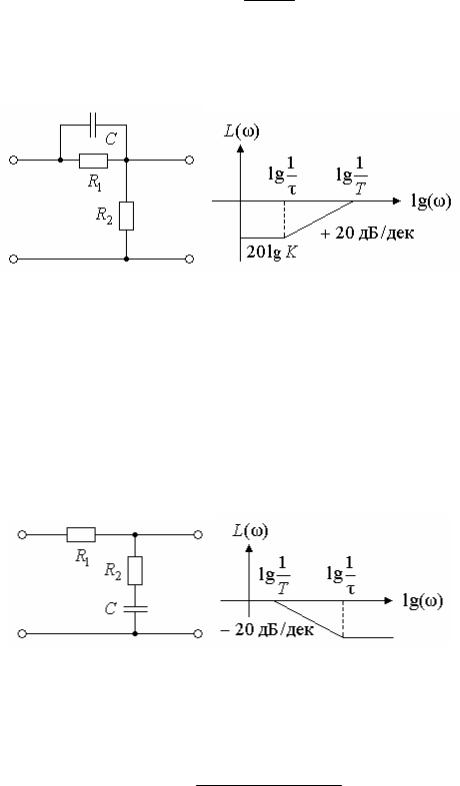
Пример 11.1. Пассивные корректирующие звенья. Форсирующее (пассивно-дифференцирующее) звено (рис. 11.2).
W(p) k τp 1,
где |
Tp 1 |
|
|
k T /τ R1 /(R1 R2); |
τ R1C; T R1R2C/(R1 R2) τ. |
а |
б |
Рис. 11.2
Замедляющее (пассивно-интегрирующее) звено (рис. 11.3).
|
W(p) k |
τp 1 |
, |
|
|
|
|||
где |
|
Tp 1 |
||
|
|
|
|
|
k 1; |
τ R2C; |
T (R1 R2)C τ. |
||
а |
б |
Рис. 11.3
Интегро-дифференцирующее звено (рис. 11.4).
W(p) k (τ1p 1)(τ2 p 1), (T1p 1)(T2 p 1)
где
245
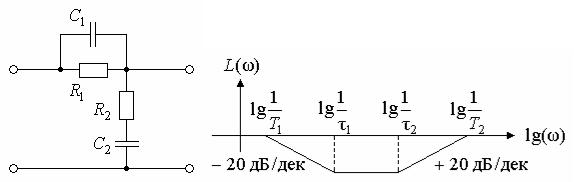
τ1 R1C1; |
τ2 R2C2; |
T1T2 τ1τ2; |
T1 T2 τ1 (1 R1 /R2)τ2. |
а |
б |
|
Рис. 11.4 |
11.1.3. Параллельные корректирующие звенья. Рассмотренные выше корректирующие звенья имеют в числителе передаточной
функции |
сумму |
пропорционального, |
дифференцирующего |
||
и интегрирующего |
слагаемых. Поэтому |
эти звенья |
можно |
||
представить |
в |
виде |
параллельно |
соединенных |
звеньев |
соответствующего действия.
Параллельные корректирующие звенья используются в тех случаях, когда необходимо осуществить сложный закон управления с введением производных, интегралов и других функций от ошибки ε в САУ.
Введение производных ε(t), ε(t) и др. соответствует поднятию верхних частот и преследует цель увеличить запас устойчивости системы.
Введение интегралов от ошибки управления ε(t)dt
соответствует поднятию нижних частот и преследует цель уменьшить значение установившейся ошибки управления или сделать ее равной нулю.
В системах автоматического управления в зависимости от вида примененной параллельной коррекции регуляторы классифицируются на следующие типы: пропорциональный (П-регулятор), пропорционально-дифференцирующий (ПД-регу-
лятор), |
пропорционально-интегрирующий |
(ПИ-регулятор) |
и пропорционально-интегро-дифференцирующий |
(ПИД-регулятор). |
|
Соответственно говорят об одноименных алгоритмах или законах управления.
246
П-алгоритм управления |
|
|
|
|
|
|
|
|
|
|
|
u(t) kп ε(t). |
|
|
(11.9) |
||||||||
ПД-алгоритм управления |
|
|
|
|
|
dε(t) |
|
|
|
|
|
u(t) k |
п |
ε(t) T |
. |
|
|
(11.10) |
|||||
|
|
|
|||||||||
|
|
|
|
д |
dt |
|
|
|
|||
ПИ-алгоритм управления |
|
|
|
1 t |
|
|
|
||||
|
|
|
|
|
|
|
|
||||
u(t) kп ε(t) |
|
|
ε(t)dt. |
|
|
(11.11) |
|||||
T |
|
|
|||||||||
ПИД-алгоритм управления |
|
и 0 |
|
|
|
||||||
t |
|
|
|
|
|
||||||
|
|
1 |
|
|
dε(t) |
. |
(11.12) |
||||
u(t) kп ε(t) |
|
ε(t)dt Tд |
|
||||||||
T |
dt |
||||||||||
|
|
|
и 0 |
|
|
|
|
|
|||
Здесь u(t) – выходной сигнал управляющего устройства.
11.1.4. Корректирующие обратные связи. Корректирующие устройства в виде корректирующих обратных связей (ОС) находят широкое распространение вследствие удобства технической реализации и обладают следующими достоинствами:
–простота – вследствие того, что на вход элемента ОС поступает обычно сигнал высокого уровня с выхода САУ, что не только не требует усилителей, но, напротив, требует ослабления сигнала для его согласования с входным сигналом;
–в реальной САУ, как правило, всегда имеют место нелинейности, которые при охвате САУ отрицательной ОС существенно ослабляют свое влияние на процессы управления, что дает возможность улучшить переходной процесс в САУ по сравнению с другими видами корректирующих устройств;
–отрицательная ОС дает лучший эффект, когда в САУ вследствие действия внешних факторов изменяются параметры САУ – коэффициенты усиления, постоянные времени, т. е. эта ОС стабилизирует параметры охваченной части САУ.
При охвате звена с передаточной функцией W0(p) обратной
связью с передаточной функцией Wос(p) получим передаточную функцию замкнутой системы (рис. 11.5)
W(p) |
W0(p) |
, |
(11.13) |
|
1 W0(p)Woc(p)
247
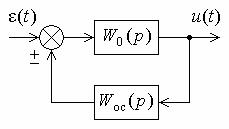
где плюс в знаменателе соответствует отрицательной (ООС), а минус – положительной (ПОС) обратным связям.
Рис. 11.5. Корректирующая обратная связь
Корректирующие обратные связи, помимо классификации на отрицательные и положительные, делятся на жесткие и гибкие. Жесткая обратная связь (ЖОС) осуществляется статическим звеном с передаточной функцией Wос(p) kос, а гибкая обратная связь (ГОС) – дифференцирующим звеном с передаточной функцией Wос(p) kосp.
В последнем случае Wос(0) 0 и, следовательно, в статике сигнал обратной связи отсутствует, т. е. гибкая обратная связь действует только в динамике, с чем и связано ее наименование.
Жесткие корректирующие обратные связи. Рассмотрим действие идеальной жесткой обратной связи. Ее передаточная функция
|
|
Wос(p) kос. |
(11.14) |
||||
В случае если эта обратная связь охватывает простое |
|||||||
апериодическое звено с передаточной функцией |
|||||||
|
W (p) |
k0 |
|
|
|
||
|
|
|
|
|
|||
|
0 |
T0 p 1 |
|
|
|||
по (11.13), получим |
|
|
|
|
|||
|
k0 |
|
|
|
k |
|
|
W(p) |
|
|
|
, |
|||
|
|
|
|
||||
|
T0 p 1 k0koc |
Tp 1 |
|||||
где
k k0 /(1 k0kос); T T0 /(1 k0kос).
Отсюда следует, что охват апериодического звена жесткой обратной связью, не изменяя структуры звена, изменяет коэффициент передачи и постоянную времени в (1 k0kос) раз, т. е. они уменьшаются в случае отрицательной ОС и увеличиваются при
248
