

2.МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕЛИНЕЙНЫХ САУ
2.1.Особенности характеристик соединений нелинейных звеньев
Внелинейных системах преобразование сигнала описывается в общем случае дифференциальным или интегральным нелинейным уравнением и может быть выражено некоторым оператором
преобразования . Если входной сигнал x(t), а выходной z(t), то
z(t) {x(t)}. |
(2.1) |
В зависимости от характера нелинейности и от динамических свойств звена оператор может выражаться достаточно сложно. В отдельных случаях преобразование сигнала нелинейным звеном может быть представлено в виде последовательного воздействия линейного оператора W(p), выражающего динамические свойства звена, и нелинейного оператора f , выражающего статическое преобразование сигнала. Такое представление соответствует эквивалентной схеме, состоящей из последовательного соединения линейного динамического и нелинейного статического звеньев.
В зависимости от последовательности действия линейного и нелинейного операторов имеет место различное преобразование сигнала. Так, если
z (t) {x(t)} f |
L 1{W(p)L[x(t)]} , |
|
|
||
1 |
1 |
|
|
|
(2.2) |
|
1 |
|
|
||
|
W(p)L{f[x(t)]} , |
|
|
||
z2(t) 2{x(t)} L |
|
|
|
||
то в общем случае
z2(t) z1(t).
Здесь L и L 1 – прямое и обратное преобразования Лапласа. Эквивалентные схемы, соответствующие двум видам
преобразования, показаны на рис. 2.1, а, б.
Так как z2(t) z1(t), то при последовательном соединении нелинейного статического и линейного динамического звеньев их перестановка недопустима. Исключение представляет звено запаздывания τ, для которого W(p) e pτ и
L 1{e pτL[x(t)]} x(t τ). |
|
В этом случае |
|
z1(t) f[x(t τ)] z2(t) |
(2.3) |
33
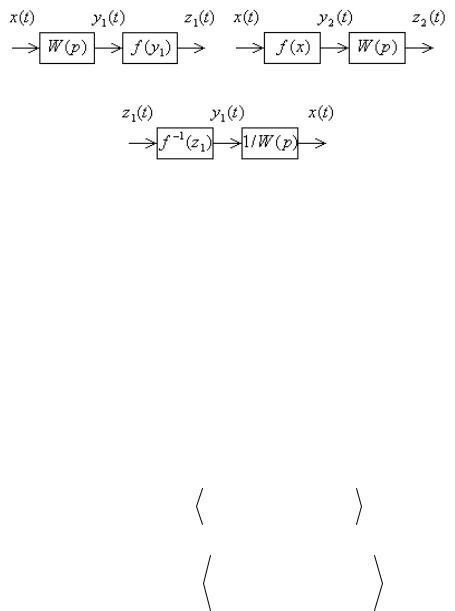
и перенос звена запаздывания через нелинейное статическое звено f (x) не изменяет свойств рассматриваемой системы.
а |
б |
в
Рис. 2.1
Для записи решения уравнения (2.1) относительно переменной
|
|
|
1 |
, соответствующий условию |
|||||
x(t) вводится обратный оператор |
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
Тогда |
{ [x(t)]} x(t). |
|
|
||||||
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
(2.4) |
||
|
x(t) |
{z(t)}, |
|
||||||
если решение уравнения (2.2) для заданного z(t) существует. |
|
||||||||
Если 1 – прямой оператор последовательного соединения |
|||||||||
линейного динамического и нелинейного статического звеньев |
|
||||||||
1{x(t)} f |
L 1{W(p)L[x(t)]} , |
|
|||||||
то обратный оператор |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
1 |
|
||
1 {z(t)} L |
|
|
|
|
L{f |
|
[z(t)]} . |
(2.5) |
|
|
|
|
|
|
|||||
|
|
W(p) |
|
|
|
||||
Здесь символом |
f 1 обозначена нелинейная функция, обратная |
||||||||
f . При этом |
|
|
|
|
|
|
|
|
|
|
f 1{f (x)} x. |
|
|
1 и |
|||||
Эквивалентные |
схемы, |
соответствующие прямому |
|||||||
1 |
|
|
|
|
|
|
|
|
|
обратному 1 операторам, показаны на рис. 2.1, а, в. |
|
||||||||
При рассмотрении статики нелинейных систем сигналы x и z не зависят от времени, а линейное звено может рассматриваться как пропорциональное и объединяться с нелинейным статическим звеном.
34

При выводе эквивалентных характеристик различных соединений нелинейных статических звеньев исходят из трех видов соединений: а) последовательного, б) параллельного согласного, в) параллельного встречного.
2.2. Статические характеристики последовательного соединения нелинейных звеньев
При последовательном соединении нелинейных звеньев выходная величина одного звена является входной величиной другого.
Рис. 2.2
При последовательном соединении n звеньев (рис. 2.2) для каждого соединения
xi 1 zi |
(2.6) |
и так как zi f (xi), то |
|
xi 1 fi(xi) ; |
(2.7) |
Решая совместно, n нелинейных уравнений вида (2.7) получим для последовательного соединения n звеньев следующую нелинейную функцию, выражающую характеристику z(x) zn(x):
n 1
z(x) fn{fn 1 [ f1(x)]}. (2.8)
Определение общей характеристики z(x) может быть сведено к проведенному n 1 раз нахождению эквивалентных характеристик двух последовательно соединенных звеньев и определенно z2(x1),
z3(x1) и т. д. до zn(x1).
Нахождение результирующей характеристики двух или трех последовательно соединенных звеньев удобно находить с помощью метода четырех квадрантов. Исходные характеристики располагаются в первом, втором и третьем квадрантах, а результирующая характеристика получается в четвертом квадранте.
35
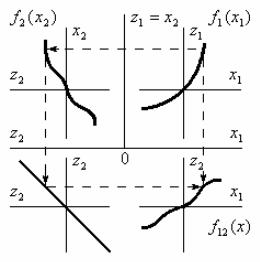
Рис. 2.3
Графическое построение характеристики z2 f12(x1) при заданных характеристиках z1 f1(x1) и z2 f2(x2) показано на рис. 2.3. При построении, выполняемом в четырех квадрантах, удобно пользоваться вспомогательным третьим квадрантом с прямой z2(z2), облегчающим переход от оси z2 в характеристике z2(x2) к оси z2 в характеристике z2(x1). Производя такое построение n раз, можно найти результирующую характеристику zn(x1) f1n(x1).
При изменении последовательности соединений звеньев в большинстве случаев результирующая характеристика изменяется.
Пример 2.1. Найти характеристику последовательного
соединения нелинейных звеньев |
типа |
«зона |
нечувствительности» |
|||
z1 f1(x1) |
и |
ограничение |
z2 f2(x2) |
при |
различной |
|
последовательности их соединения. |
|
|
|
|
||
Решение. |
На |
рис. 2.4 выполнены |
два |
варианта |
построения |
|
характеристик таких соединений. На рис. 2.4, б построена
зависимость |
z2(x1) f2[f1(x1)] |
для соединения, изображенного на |
рис. 2.4, а. |
Соответственно |
на рис. 2.4, г – зависимость |
z1(x2) f1[f2(x2)], для соединения, показанного на рис. 2.4, в. Из построения видно, что в обоих случаях получено звено типа «ограничение с зоной нечувствительности», однако значения выходной величины, соответствующей ограничению zс, и входной
величины, соответствующей зоне нечувствительности |
xс, |
36 |
|
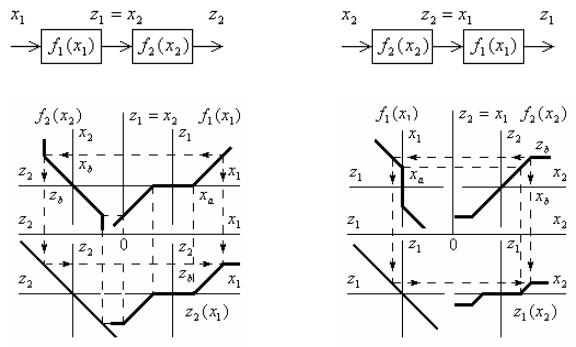
оказываются различными. В первом случае они совпадают со
значениями для |
исходных нелинейностей: zc zb |
и xc xa, а |
во |
|
втором случае |
они |
существенно отличаются: |
zc zb xa, |
а |
xc xa /k2. При zb xa |
второе соединение приводит к разрыву цепи |
|||
передачи сигнала. |
|
|
|
|
а |
в |
б |
г |
Рис. 2.4
Пример 2.2. В последовательном соединении нелинейного звена с однозначной характеристикой, интегрирующего звена и звена типа «упор» (рис. 2.5, а) необходимо два нелинейных звена привести к одному нелинейному звену.
Решение. Такая задача может быть решена, если ввести понятие звена, характеристика которого выражает связь не только между сигналами, но и между их производными или интегралами по времени. Заменяя звено z(x) на рис. 2.5, а схемой, изображенной на рис. 2.5, б учитывая, что соединенные последовательно интегрирующее и дифференцирующее звенья взаимно компенсируются, получим эквивалентную схему, показанную на рис. 2.5, в. Здесь нелинейные звенья x(γ) и z(x,z) соединены последовательно и могут быть заменены одним нелинейным звеном с характеристикой z(γ,z), показанным на риc. 2.5, г.
37
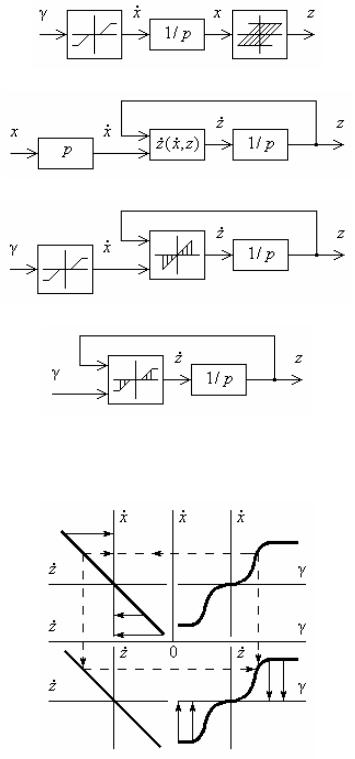
Построение характеристики z(γ,z) выполнено на рис. 2.6.
а
б
в
г
Рис. 2.5
Рис. 2.6
38
Взаимно обратные звенья. При последовательном соединении двух нелинейных звеньев с характеристиками f и f 1 может оказаться, что результирующая характеристика получается линейной, а коэффициент усиления системы равен единице. Два нелинейных звена, последовательное соединение которых образует пропорциональное звено с единичным коэффициентом усиления, называются взаимно обратными.
Для двух взаимно обратных нелинейных звеньев c
характеристиками z |
f (x |
) и z |
2 |
f |
1(x |
2 |
) справедливо равенство |
|
1 |
1 |
|
|
|
|
|
||
|
|
f 1[ f (x |
)] x . |
(2.9) |
||||
Перемена местами |
|
|
1 |
|
1 |
не изменяет общей |
||
таких звеньев |
||||||||
характеристики системы, т. е. для них выполняется принцип коммутативности и
f[ f 1(x2)] x2. |
(2.10) |
Это свойство справедливо только для |
монотонных |
характеристик, не имеющих горизонтальных или вертикальных участков.
Пример 2.3. Найти характеристику нелинейного звена z1 f1(x1), которое необходимо включить последовательно с звеном типа «люфт» z2 f2(x2) для того, чтобы результирующая характеристика последовательного соединения была линейной и выражалась прямой z2(x1) x1.
Решение. Для этого из построения известных характеристик z2 f2(x2) и z2(x1) x1 (рис. 2.7) обратным путем можно найти требуемую характеристику z1 f1(x1). Из приведенного на чертеже построения видно, что для выполнения условия z2(x1) x1 необходимо, чтобы две характеристики z1 f1(x1) и z2 f2(x2) в двух квадрантах координат x1, z1 x2, z2 представляли собой кривые, зеркально симметричные относительно оcи z1 x2.
39
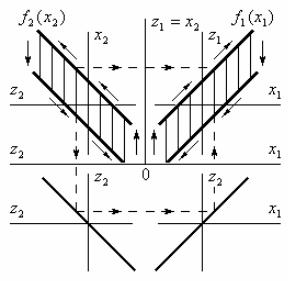
Рис. 2.7
2.3. Статические характеристики параллельного согласного соединения нелинейных звеньев
При параллельном согласном соединении нелинейных звеньев на их входы подается одна и та же величина, а выходные величины суммируются с соответствующими знаками.
Если параллельно соединены n звеньев, то входная величина:
x x1 x2 xn, |
(2.11) |
a выходная величина |
|
n |
|
z f (x) fi(x). |
(2.12) |
i 1 |
|
Из выражения (2.12) видно, что характеристика параллельного согласного соединения ряда нелинейных звеньев может быть получена путем непосредственного суммирования соответствующих ординат составляющих характеристик.
Схема параллельного согласного соединения n нелинейных звеньев показана на рис. 2.8.
40
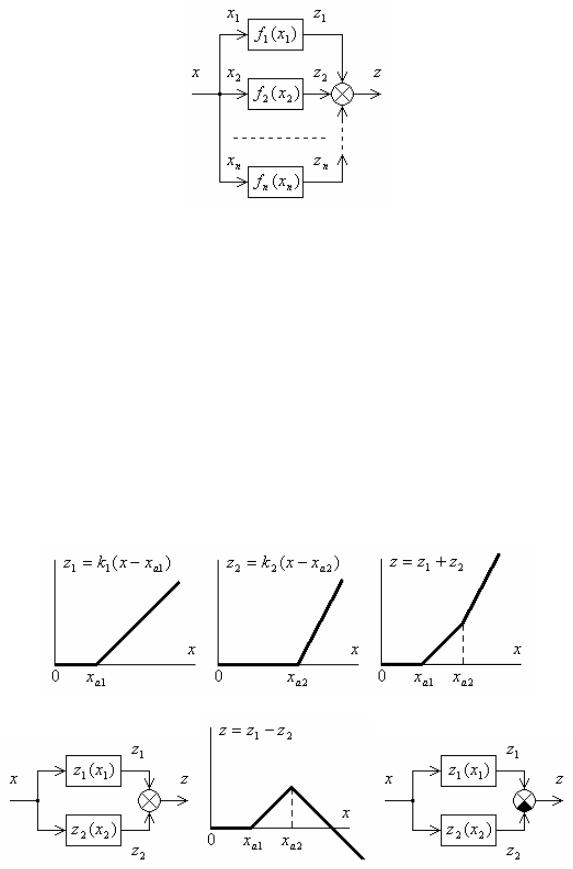
Рис. 2.8
Пример 2.4. Найти характеристику параллельного согласного соединения нелинейных звеньев типа «зона нечувствительности» z1 и z2 соответственно c зонами нечувствительности xa1 и xa2 c крутизной k1 и k2 (риc. 2.9, а, б).
Решение. На рис. 2.9, в построена характеристика z(x) z1 z2 в случае, когда в суммирующем узле сигналы z1 и z2 складываются с одинаковыми знаками (рис. 2.9, г). Соответственно на рис. 2.9, д построена характеристика z(x) z1 z2 для случая, когда в суммирующем узле сигналы z1 и z2 складываются о разными знаками (рис. 2.9, е).
а |
б |
в |
г |
д |
е |
Рис. 2.9
41
Из рассмотрения участка характеристики (рис. 2.9, д) при x xa2 видно, что если k1 k2, то наклон характеристики равен нулю и она соответствует звену типа «зона нечувствительности с ограничением».
Пример 2.5. Звено с характеристикой z1(x1), полученное в примере 2.3 (см. рис. 2.7), представить в виде параллельного согласного соединения двух более простых типовых звеньев.
Решение. Рассматривая звено типа «упор» с прямоугольной характеристикой, легко заметить, что параллельное соединение этого звена с пропорциональным звеном, имеющим единичный коэффициент усиления, дает звено с требуемой, характеристикой z1(x1).
Взаимно дополнительные звенья. При параллельном согласном соединении двух нелинейных звеньев и соответствующем выборе их характеристик может оказаться, что результирующая характеристика линейна и коэффициент усиления равен единице. Такие два нелинейных звена, параллельное согласное соединение которых образует пропорциональное звено, называют взаимно дополнительными. Оба звена равноценны в этом соединении.
Для двух взаимно дополнительных нелинейных звеньев справедливо равенство:
или |
f1(x) f2(x) x |
(2.13) |
|||||||
|
x |
|
x |
|
|
|
|
||
f (x) |
|
f |
2 |
(x). |
(2.14) |
||||
|
|
||||||||
1 |
2 |
2 |
|
|
|
||||
Из равенства (2.14) следует, что условием взаимной дополнительности характеристик z1 f1(x) и z2 f2(x) является равенство расстояний от этих характеристик по оси z до прямой z x/2 (рис. 2.10). Это условие называется эквидистантностью по оси z относительно прямой z x/2.
42
