

Рис. 2.10
Если дана нелинейная характеристика f (x), то дополнительную характеристику будем обозначать f (x). Уравнение (2.13), связывающее две взаимно дополнительные характеристики, в этом случае имеют вид:
f (x) f (x) x. |
|
|
|
(2.15) |
|||
Пример 2.6. Найти характеристику |
|
|
(x), дополнительную по |
||||
f |
|||||||
отношению к заданной характеристике |
f (x) типа «ограничение с |
||||||
линейной зоной xb 1/2 c единичной крутизной». |
|
|
|
|
|||
Решение. Проводя прямую z x/2 |
(штриховая линия на рис. |
||||||
2.11), из условия эквидистантности по |
оси z относительно |
этой |
|||||
прямой получаем требуемую характеристику |
|
|
(x). |
Эта |
|||
f |
|||||||
характеристика описывает звено типа «зона нечувствительности» с xa xb 1/2.
Рис. 2.11
Таким образом, звенья типов «зона нечувствительности» и «ограничение» при xa xb при единичной крутизне имеют взаимно дополнительные характеристики.
43
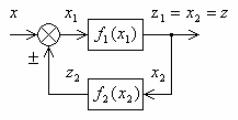
2.4. Статические характеристики параллельного встречного соединения нелинейных звеньев
При параллельном встречном соединении двух звеньев (рис. 2.12) выходной сигнал первого звена (прямой связи) подается на вход второго звена (обратной связи), а выходной сигнал второго звена с соответствующим знаком суммируется с входным сигналом и подается на вход первого звена. Общим выходным сигналом является выход звена прямой связи. Обратная связь в зависимости от знака сигнала, поступающего в суммирующий узел, может быть отрицательной или положительной.
Рис. 2.12 |
|
Соответственно уравнения замыкания имеют вид |
|
x1 x z2, |
(2.16) |
где знак плюс соответствует положительной обратной связи, а знак минус – отрицательной;
При этом |
|
z z1 x2. |
(2.17) |
Для построения общей характеристики |
параллельного |
встречного соединения z(x) необходимо уравнения (2.16) и (2.17) рассматривать совместно с характеристиками нелинейных звеньев f1(x1) и f2(x2).
Тогда, преобразуя (2.16) с учетом (2.17), получим |
|
|||
x f 1 |
(z) f |
2 |
(z). |
(2.18) |
1 |
|
|
|
|
В этом уравнении знак минус соответствует положительной, а знак плюс – отрицательной обратной связи.
По уравнению (2.18) легко построить общую характеристику z(x) или x(z).
Пусть характеристики f1(x1) и f2(x2) имеют вид графиков,
44
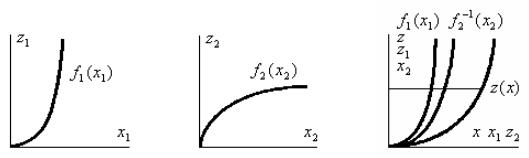
построенных на рис. 2.13, а, б. Тогда для получения z(x) |
необходимо |
||||||||||
построить кривые |
f (x ) z(x ), |
f |
1 |
(z |
2 |
) z(z |
2 |
) |
и затем |
||
|
1 |
1 |
1 |
|
2 |
|
|
|
|
||
алгебраически сложить абсциссы этих кривых в соответствии с уравнением (2.18).
а |
б |
в |
|
Рис. 2.13 |
|
Для отрицательной обратной связи на рис. 2.13, в выполнено |
||
построение z(x) |
путем суммирования абсцисс графиков z1 f1(x1) и |
|
x2 f2(z2). |
|
|
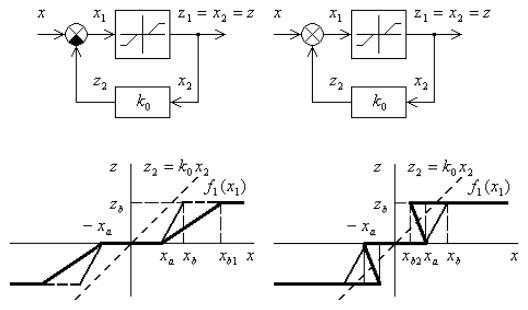
Пример 2.7. Построить характеристику звена типа «ограничение с зоной нечувствительности» z1 f1(x1), охваченного отрицательной (рис. 2.14, а) или положительной (рис. 2.14, б) жесткой обратной связью с коэффициентом усиления k0.
Решение. В этом случае характеристика обратной связи линейна z2 k0x2 или x2 z2 /k0. Построение результирующей характеристики для обоих случаев показано на рис. 2.14, в, г. Как видно из построения, в первом случае результирующая характеристика однозначна и соответствует звену типа «ограничение с зоной нечувствительности». Пределы линейной зоны усиления при этом возрастают с xb xa до xb1 xa xb1 xa , где xb1 xb k0zb . Во втором случае результирующая характеристика при k0zb xb xa становится неоднозначной и соответствует трехпозиционному реле с гистерезисом. В этом случае ширина петли гистерезиса равна xa xb2 k0zb xb xa.
45
а |
б |
в |
г |
|
Рис. 2.14 |
Пример 2.8. То же, что и в примере 2.7, но только для звена типа «двухпозиционноереле без гистерезиса».
Решение. В этом случае, производя построения, аналогичные примеру 2.7, легко убедиться, что при отрицательной обратной связи при k0zb x k0zb для каждого значения x не существует определенного значения z.
Реле находится в режиме непрерывных переключений, частота которых зависит от паразитных параметров системы. При этом постоянная составляющая сигнала на выходе может с достаточной точностью совпадать с линейным законом z x/k0.
Такой вибрационный режим носит название скользящего режима.
При положительной обратной связи общая характеристика становится двузначной и имеет вид зависимости, для которой xa k0zb.
Условие линейности. Подобно ранее рассмотренным соединениям звеньев можно определить: какова должна быть нелинейность в цепи обратной связи z2(x2) для того, чтобы коэффициент передачи равнялся единице или z(x) x?
Пусть знак обратной связи отрицателен. Тогда уравнение 2.18
46
примет вид
|
|
|
|
|
|
|
x z f 1 |
(z) f |
2 |
(z) |
|
(2.19) |
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
или в соответствии с 2.15 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
f |
|
(z) z f 1 |
|
|
1 |
(z), |
(2.20) |
|||
|
|
|
|
|
2 |
(z) f |
|||||||||
где f 1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|||
(z) и |
|
|
(z) взаимно дополнительны. |
|
|||||||||||
f |
|
||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
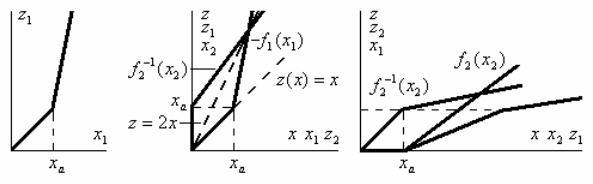
Пример 2.9. Пусть нелинейная характеристика прямой связи z1 f1(x1) выражается зависимостью (рис. 2.15, а)
|
|
x1 |
при x1 xa; |
|
||||
z1 kx |
(k 1)x |
a |
при x |
x |
a |
. |
(2.21) |
|
|
1 |
|
1 |
|
|
|
||
Найти характеристику нелинейной обратной связи, компенсирующей нелинейность прямой связи, т. е. делающей систему линейной z x.
а |
|
|
|
б |
|
|
|
в |
|
|
|
|
|
|
Рис. 2.15 |
|
|
|
|||
На рис. 2.15, б согласно уравнению (15.19) построена |
||||||||||
характеристика |
x2 f2 1(z2). |
Как |
видно |
из построения, |
она |
|||||
получается из |
характеристики |
|
f1(x1) на |
основании |
условия |
|||||
эквидистантности по оси x относительно |
прямой z 2x. |
Эта |
||||||||
характеристика выражается уравнением |
|
|
|
|||||||
|
|
|
01 при x1 xa; |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
z2 |
k 1 |
(x |
x |
a |
) при x x . |
(2.22) |
|||
|
|
|
|
|||||||
|
|
2 |
|
1 |
a |
|
|
|||
|
k |
|
|
|
|
|
|
|
||
В отличие от параллельного согласного соединения перемена местами нелинейностей прямой и обратной связи существенно
47
изменяет общую нелинейную характеристику системы. Если в рассматриваемом примере поменять местами нелинейности прямой и обратной связи и построить суммарную характеристику, то это построение изобразится графиками, показанными на рис. 2.15, в. Как видно из построения, результирующая характеристика z(x) существенно отличается от полученной ранее прямой z(x) x (рис. 2.15, б)
2.5. Преобразования структурных схем нелинейных систем
Введение в систему нелинейных звеньев несколько ограничивает возможности структурных преобразований, однако и в этом случае они имеют большое значение для синтеза и построения моделей различных систем.
Рассмотрим правила преобразования линейных систем и возможность их распространения на нелинейные системы.
Виды преобразований:
1)перемещение суммирующего узла через узел разветвления;
2)перемещение линейного звена через узел разветвления;
3)перемещение линейного звена через суммирующий узел;
4)перемещение линейного звена через другое линейное звено;
5)эквивалентность встречных параллельных соединений. Невозможность распространения всех правил структурного
преобразования линейных систем на нелинейные системы связана с невыполнением в нелинейных системах двух принципов: принципа наложения (суперпозиции) и принципа коммутативности. Невыполнение принципа наложения исключает возможность применения третьего вида преобразования, а невыполнение принципа коммутативности – применение четвертого вида преобразований. Первые два вида преобразования не противоречат этим двум принципам и, следовательно, вполне могут быть применены для преобразования нелинейных систем. То же относится и к пятому виду преобразований.
Для нелинейных систем полностью могут быть применимы два правила перемещения суммирующего узла через узел разветвления.
Первое правило. При перемещении суммирующего узла через узел разветвления по направлению ветвления (или по направлению передачи сигнала) необходимо в отходящих от разветвления ветвях
48
добавить такие же, как и перемещаемый узел, суммирующие узлы. Второе правило. При перемещении суммирующего узла через
узел разветвления против направления ветвления (или против направления передачи сигнала) необходимо в отходящих от разветвления ветвях добавить суммирующие узлы, отличающиеся от перемещаемого узла знаками суммируемых величин.
Третье правило. При перемещении звена через узел разветвления по направлению ветвления (по направлению передачи сигнала) необходимо в отходящих от узла ветвях добавить звенья с оператором перемещаемого звена.
Четвертое правило. При перемещении звена через узел разветвления против направления ветвления (против направления передачи сигнала) необходимо в отходящих от узла ветвях добавить звенья с обратными операторами перемещаемого звена.
Пример 2.10. Переместить безынерционное нелинейное звено z(x) через узел разветвления по направлению ветвления.
Решение. На рис. 2.16, а, б показано применение третьего правила для перемещения нелинейного звена с кусочно-линейной характеристикой.
Пример 2.11. Переместить инерционное нелинейное звено,
состоящее |
из последовательно линейного W(p) и |
нелинейного |
z f (y) |
звеньев, через узел разветвления против |
направления |
ветвления.
Решение. Применение четвертого правила для этой цели показано на рис. 2.16, в, г.
Здесь нелинейная характеристика y f 1(z) обратная по отношению к z f (y), а W 1(p) 1/W(p).
49
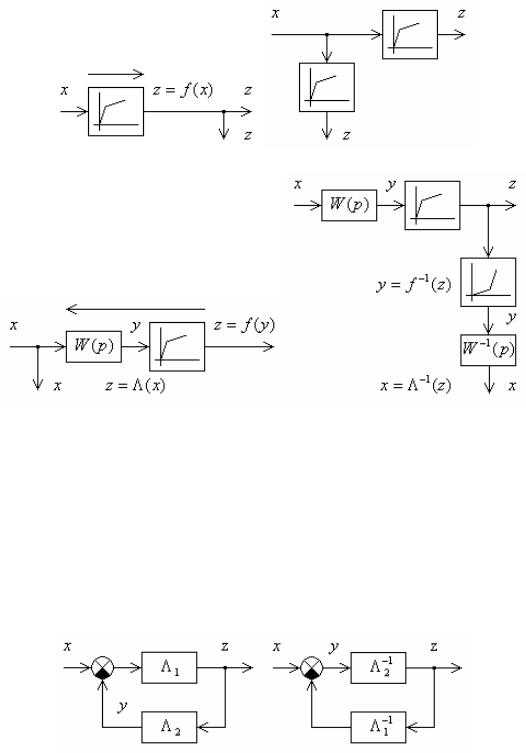
а б
в г
Рис. 2.16
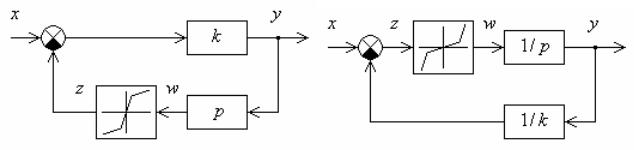
На основе понятия обратных операторов можно показать, что схема с прямой 1 и обратной 2 связями, изображенная на рис. 2.17, а, эквивалентна схеме (рис. 2.17, б), построенной из звеньев с
обратными операторами |
1 |
и |
1 |
, если звено |
1 |
включено вместо |
|
1 |
2 |
1 |
|||||
1 |
– вместо звена 1. |
|
|
||||
звена 2 ,а звено 2 |
|
|
|||||
а |
|
|
б |
|
Рис. 2.17 |
|
|
Действительно, записав уравнение замыкания |
|||
z 1[x 2(z)] |
(2.23) |
||
или |
|
|
|
1 |
(z) x 2 |
(z), |
(2.24) |
1 |
|||
50 |
|
|
|
после элементарных преобразований получим
1 |
1 |
(2.25) |
z 2 [x 1 (z)], |
||
что соответствует схеме, показанной на рис. 12.17, б. |
|
|
Таким образом, на основе введения обратных операторов можно |
||
сформулировать еще одно правило преобразования. |
|
|
Пятое правило. В системе с |
отрицательной обратной |
связью |
можно менять местами звенья, включенные в цепи прямой и обратнойсвязи, с заменой операторов звеньев обратными.
Применение этого правила важно в том случае, когда необходимо перейти от нереализуемых или трудно реализуемых структурных схем к схемам реализуемым.
а |
б |
Рис. 2.18
Пример 2.12. Для схемы (рис. 2.18, а), состоящей из пропорционального звена k, охваченного обратной связью по знаку производной, т. е. последовательным соединением дифференцирующего звена p и нелинейного звена z(w), найти лучше реализуемую эквивалентную схему, состоящую из звеньев с обратными характеристиками.
Решение. Применение пятого правила приводит к эквивалентной схеме (рис. 2.18, б).
Нелинейные характеристики w(z) и z(w) могут быть описаны кусочно-линейными зависимостями
|
αz |
при| z| za; |
|
|
αza (z za)при z za; |
(2.26) |
|
w |
|||
αza (z za)при z za.
51
ω
при|ω| αza;
α
|
|
|
ω αz |
a |
|
|
|
z |
za |
|
приω αza; |
(2.27) |
|||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
ω αza |
|
|
|
|
za |
|
приω αza. |
|
||||
|
|
|
|||||
|
|
|
|
|
|
|
|
При α 0 и β эта характеристика переходит в z zasignw. Так как реализация интегрирующего звена осуществляется точнее, чем дифференцирующего звена, схема, изображенная на рис.
2.18, б, более удобна для выполнения.
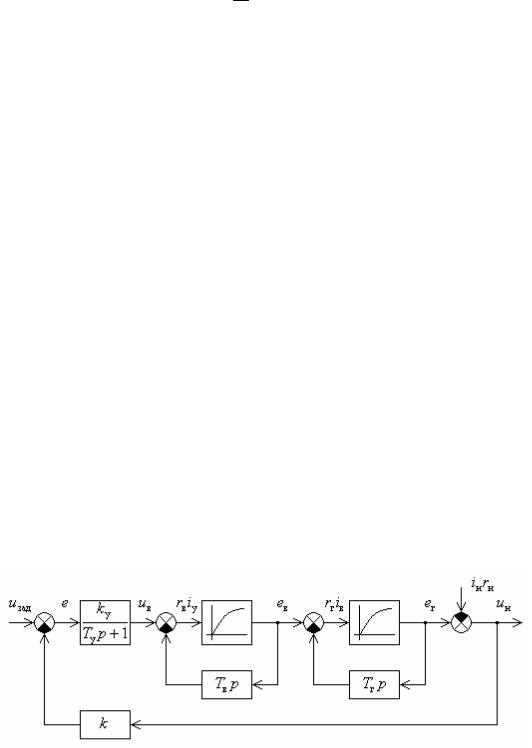
Пример 2.13.. Для структурной схемы стабилизатора напряжения (см. рис. 2.19) найти эквивалентную схему, не содержащую дифференцирующих звеньев:
Решение. Каждое из двух нелинейных звеньев, охваченных дифференцирующей обратной связью, в соответствии с пятым правилом преобразования эквивалентно интегрирующему звену, охваченному нелинейной обратной связью с характеристикой, обратной характеристике исходного звена прямой связи. Таким образом, для структурной схемы рис. 2.19 может быть получена эквивалентная схема, (рис. 2.20), более удобная для моделирования процессов в системе.
Рис. 2.19
52
