
2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ CАУ
2.1. Постановка задачи. Структурная схема САУ
Целью рассмотрения системы автоматического управления может быть решение одной из двух задач – задачи анализа системы или задачи ее синтеза. В первом случае дается система, включая значения параметров, и требуется определить ее свойства. Во втором случае, наоборот, задаются свойства, которыми должна обладать система, т. е. требования к ней, и необходимо создать систему, удовлетворяющую этим требованиям. Очевидно, что задача синтеза много сложнее задачи анализа уже из-за ее неоднозначности.
В самом общем виде порядок исследования САУ в обоих случаях включает математическое описание системы, исследование ее установившихся режимов и исследование переходных режимов.
Математическое описание системы, т. е. получение ее математической модели, начинается с разбиения ее на звенья и описания этих звеньев. Это описание может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные величины звена, либо графически в виде характеристик, описывающих ту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом, на основании которых и исследуется система.
Выше при рассмотрении принципа действия систем автоматического управления было дано понятие о функциональной схеме САУ. В функциональной схеме система разбита на звенья исходя из выполняемых ими функций, т. е. назначения (см.
рис. 1.2, б).
Для математического описания систему разбивают на звенья по другому принципу, а именно исходя из удобства получения этого описания. Для этого систему следует разбивать на возможно более простые звенья, но вместе с тем необходимо, чтобы они обладали направленностью действия.
Звеном направленного действия называется звено, передающее воздействие только в одном направлении – со входа на выход, так что изменение состояния такого звена не влияет на состояние предшествующего звена, работающего на его вход. В результате при разбиении системы на звенья направленного действия
32
математическое описание каждого такого звена может быть составлено без учета связей его с другими звеньями. Соответственно математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связи между звеньями.
Врезультате разбиения САУ на звенья направленного действия
иполучения математического описания звеньев составляется структурная схема системы, которая является ее математической моделью. Структурная схема системы состоит из прямоугольников,
изображающих звенья схемы, и стрелок, |
соединяющих |
выходы |
и входы звеньев согласно связям между |
звеньями в |
системе. |
Стрелками показываются также внешние воздействия, приложенные к отдельным звеньям системы. Каждому звену структурной схемы придается описывающее его уравнение или характеристика. Эти уравнения обычно записываются прямо на схеме внутри изображающих звенья прямоугольников в виде передаточных функций (см. п. 2.4). Получение структурной схемы является конечной целью математического описания системы.
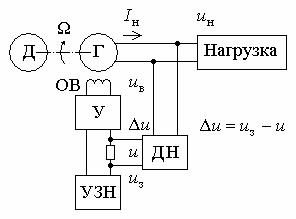
Рис. 2.1. Замкнутая система управления напряжением генератора постоянного тока
В качестве примера рассмотрим разбиение на звенья системы автоматического регулирования напряжения генератора постоянного тока, изображенной на рис. 2.1, где Д – двигатель, Г – генератор, УЗН – устройство задания напряжения, У – усилитель, ОВ – обмотка возбуждения генератора, ДН – датчик (делитель) напряжения. При этом принято, что усилитель регулятора состоит из двух частей –
33

усилителя напряжения УН и усилителя мощности УМ. Каждый из этих усилителей обладает направленностью действия и поэтому может быть выделен в виде отдельного звена. Это показано на рис. 2.2.
Рис. 2.2. Разбиение на звенья системы автоматического регулирования напряжения
На рис. 2.2 стрелками показаны внешние воздействия – задающее воздействие Uз и возмущение в виде сопротивления нагрузки Rн на зажимах генератора. На этом же рисунке в виде кружочка, разделенного на секторы, дано условное изображение элемента сравнения, т. е. суммирующего элемента, выявляющего
разность U Uз U . |
Рядом показаны знаки сигналов (плюс у Uз |
и минус у U ). Как |
показано на рис. 2.2, обычно сектор, |
соответствующий вычитаемому сигналу, закрашивается черным цветом.
2.2. Дифференциальные уравнения. Линеаризация уравнений
Для получения математического описания системы обычно составляют описание ее отдельных элементов. В частности, для получения уравнений системы составляют уравнения для каждого входящего в нее элемента (рис. 2.3). Совокупность всех уравнений элементов и дают уравнения системы.
Рис. 2.3. Звено направленного действия
34
В общем случае звенья и системы описывают нелинейными дифференциальными уравнениями произвольного порядка
|
|
|
|
|
|
, (2.1) |
[Y(t),Y |
(t),Y(t), ,U(t),U(t),U(t), , F(t), F(t), F(t), ] 0 |
|||||
где Y(t) – |
выходная величина, |
U(t) |
– управляющее воздействие, |
|||
F(t) – возмущающее воздействие.
Уравнение (2.1), описывающее процессы в звене при произвольных входных воздействиях, называют уравнением динамики.
Пусть при постоянных входных величинах U(t) U0 и F(t) F0 процесс в звене с течением времени установится: выходная величина примет постоянное значение Y(t) Y0. Тогда уравнение (2.1) примет вид
(Y0,0, 0, ,U0,0,0, , F0,0,0, ) 0.
Это уравнение описывает статический или установившийся режим, и его называют уравнением статики.
Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой звена или элемента (а также системы) называют зависимость выходной величины от входной в статическом режиме.
Основная сложность, которая существует при выводе уравнений звеньев системы, заключается в необходимости установления допустимой степени идеализации и упрощения звеньев. Нелинейные звенья и системы во многих случаях можно линеаризовать, т. е. заменить исходные нелинейные уравнения линейными, приближенно описывающими процессы. Процесс преобразования нелинейных уравнений в линейные называют линеаризацией.
а |
б |
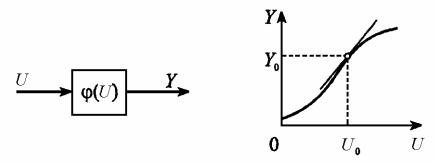
Рис. 2.4. Линеаризация статического звена
35

Рассмотрим звено, описываемое нелинейной статической зависимостью Y (U) (рис. 2.4, а). Пусть установившийся режим звена соответствует значениям входной и выходной величин U0 и Y0 (рис. 2.4, б) и отклонения U от U0 в процессе работы звена достаточно малы. В этом случае исходную нелинейную зависимость Y (U) можно разложить в ряд Тейлора в окрестностях точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получить следующую приближенную зависимость:
d
где dU 0
d |
|
||
Y (U0) |
|
|
(U U0), |
|
|||
dU 0 |
|
||
– значение производной |
функции (U) по U при |
||
подстановке в выражение этой производной U U0.
Это уравнение можно переписать в таком окончательном виде:
Y k U,
где
dU U U0; Y Y Y; k .
dU 0
Проведенная линеаризация имеет простую графическую интерпретацию: она соответствует, как показано на рис. 2.4, б, замене действительной нелинейной характеристики касательной к ней
вточке, соответствующей установившемуся режиму. Коэффициент k
вполученном уравнении равен тангенсу угла наклона этой касательной относительно оси абсцисс. Поэтому его величина может быть найдена чисто графическим построением без нахождения аналитического выражения для исходной нелинейной зависимости
(U).
Рассмотрим теперь более общий случай, когда звено описывается нелинейным уравнением, включающим производные по
времени от входной и выходной величин:
[Y(t),Y(t),Y(t), ,U(t),U(t),U(t), ] 0.
Разложив, как и прежде, нелинейную функцию, находящуюся в левой части уравнения, в ряд Тейлора в точке установившегося режима, получим следующее линейное дифференциальное уравнение для приращений переменных:
36
d |
|
d |
|
|
d |
|
|
|
||||||||
|
|
|
|
Y |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Y |
|
|
Y ... |
||||||||
dY 0 |
|
dY 0 |
dY |
0 |
|
|
(2.2) |
|||||||||
|
d |
|
|
d |
|
d |
||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
U |
|
|
U |
|
|
U ... 0. |
|||||||
|
dU |
0 |
|
dU 0 |
|
dU 0 |
|
|||||||||
Здесь |
d |
, |
|
||
dU |
0 |
|
d |
и т. д. – значения производных функции , |
||
|
|
|
|
|
|||
dU |
0 |
|
|
получающиеся при подстановке значений U0, Y0 и нулевых значений производных, соответствующих установившемуся режиму.
Показанная процедура линеаризации нелинейных звеньев приводит к приближенному описанию их линейными дифференциальными уравнениями в отклонениях (в вариациях).
Допустимость такой линеаризации ограничена следующими очевидными условиями. Во-первых, она применима только для малых отклонений, т. е. полученные в результате линеаризации уравнения пригодны для приближенного исследования только таких режимов в системах, при которых переменные величины на входе звеньев претерпевают достаточно малые отклонения от установившихся значений. При этом точность исследования растет с уменьшением отклонений.
Во-вторых, поскольку такая линеаризация основана на разложении в ряд Тейлора, она применима только к непрерывно дифференцируемым нелинейностям. Поэтому такие нелинейности называются линеаризуемыми. Нелинейные звенья, не удовлетворяющие этому требованию, называются существенно нелинейными. К существенно нелинейным звеньям, например, относятся звенья с прерывистыми характеристиками типа релейных характеристик и с неоднозначными характеристиками типа петли гистерезиса.
В теории автоматического управления принята стандартная форма записи линейных дифференциальных уравнений звеньев. При этом (2.2) в операторной форме записывается так:
(Tnn pn Tnn 11pn 1 T1p 1)y(t)
(k |
m |
pm k |
m |
pm k p k |
0 |
)u(t). |
(2.3) |
|
|
1 |
|
|
37
Здесь |
p d /dt |
– |
|
оператор |
дифференцирования |
по |
времени; |
||||||||||||||||
u(t) |
U(t) |
; |
y(t) |
Y(t) |
|
– |
приращения переменных в относитель- |
||||||||||||||||
U0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
Y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
d |
|
|
d |
U |
0 |
|
|
|
|
|||||
ных единицах; ki |
|
|
|
/ |
|
|
|
|
– коэффициенты передачи; |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
d |
|
|
d |
dU(i) |
|
0 |
dY 0 Y0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Tj |
|
|
|
/ |
|
|
– постоянные времени. |
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||
dY( j) |
0 |
dY 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Особенности |
|
|
приведенной |
формы |
записи |
заключаются |
|||||||||||||||||
в следующем. |
Выходная |
величина |
и |
ее |
производные |
находятся |
|||||||||||||||||
влевой части уравнения, а входная величина и ее производные –
вправой. Коэффициент при приращении выходной величины равен
единице в результате деления обеих частей |
уравнения |
на |
d |
. |
|
||||
Приращения переменных обозначаются |
строчными |
dY |
0 |
|
буквами |
||||
и выражены в относительных единицах. Правда, иногда более удобно использовать абсолютные значения приращений переменных. В этом случае выражения для коэффициентов передачи, стоящих в правой части уравнения, соответственно изменяются.
Коэффициенты левой части уравнения – постоянные времени
вобоих случаях остаются без изменения. Размерность их – секунда
встепени, равной порядку производной, перед которой стоит данный коэффициент.
Если ввести обозначения собственного оператора звена
Q(p) Tnn pn Tnn 11pn 1 T22 p2 T1p 1
и оператора входного воздействия
R( p) km pm km pm k2 p2 k1 p k0 ,
то линеаризованное дифференциальное уравнение звена (2.3) можно записать в более компактной форме
Q(p)y(t) R(p)u(t).
Здесь n – порядок собственного оператора, порядок звена, n m – условие физической реализации звена.
Аналогично на основе принципа суперпозиции может быть получено уравнение и при наличии возмущающего воздействия
Q(p)y(t) R(p)u(t) P(p) f (t).
38
Звенья и системы, которые описываются линейными уравнениями, называются линейными – соответственно линейными звеньями и линейными системами.
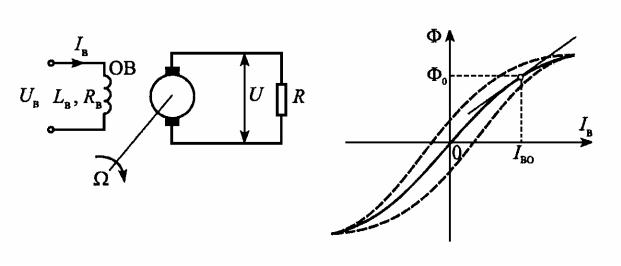
Пример 2.1. Рассмотрим в качестве примера линеаризации вывод уравнения генератора постоянного тока, показанного на рис. 2.5, а.
а |
б |
Рис. 2.5. К выводу уравнения генератора постоянного тока
Решение. Входной величиной генератора в данном случае является напряжение возбуждения Uв, а выходной – напряжение на его зажимах U . Скорость вращения якоря и величину сопротивления нагрузки Rн примем постоянными. Реакция якоря предполагается скомпенсированной и не учитывается.
Напряжение генератора
U |
Rн |
E. |
(2.4) |
|
Ra Rн |
||||
Здесь E – э. д. с. генератора; |
|
|
||
Rа – |
сопротивление цепи |
якоря |
генератора; Rн – сопротивление нагрузки (принято чисто активным). Э. д. с. генератора пропорциональна скорости вращения якоря
и магнитному потоку, т. е. |
|
|
|
E C Ф, |
(2.5) |
где Ω – |
угловая скорость вращения якоря; Ф – сцепляющаяся |
|
с якорем |
часть магнитного потока, создаваемого |
обмоткой |
|
|
39 |
возбуждения; С – коэффициент, постоянный для данной машины. Поскольку скорость вращения якоря постоянна, перепишем выражение (2.5) в виде
|
(2.6) |
E C Ф, |
|
где C C . |
|
Поток Ф является функцией тока возбуждения, т. е. |
|
Ф (Iв). |
(2.7) |
Эта зависимость нелинейная и показана на рис. 2.5, б.
В свою очередь, ток возбуждения зависит от напряжения возбуждения согласно следующему уравнению цепи возбуждения:
U |
в |
R I |
в |
wσ |
dФ |
, |
(2.8) |
|
|||||||
|
в |
|
dt |
|
|
||
|
|
|
|
|
|
|
где Uв – напряжение возбуждения; Iв – ток возбуждения; Rв – сопротивление цепи возбуждения; w – число витков обмотки возбуждения; σ – коэффициент рассеяния магнитного потока, с помощью которого полный поток, создаваемый обмоткой возбуждения, выражается в виде σФ (σ 1).
Уравнения (2.4), (2.6), (2.7) и (2.8) в совокупности определяют искомую зависимость U от Uв через промежуточные переменные E,
Фи Iв. Эта зависимость нелинейная из-за нелинейности
характеристики намагничивания генератора (2.7). Эта нелинейность связана с насыщением магнитной цепи, а также с гистерезисом.
Линеаризовать такую нелинейность по вышеизложенной методике путем перехода к малым приращениям переменных можно только, если пренебречь гистерезисом, т. е. ограничиться учетом основной кривой намагничивания, показанной на рис. 2.5, б сплошной линией. Предположим, что петля гистерезиса узка и ею заведомо можно пренебречь. Тогда, переходя к приращениям переменных, получаем следующую систему линейных уравнений
U |
|
|
Rн |
|
E; |
|||
|
|
|
|
|||||
|
|
Ra Rн |
|
|
||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
E С Ф; |
|
|
|
|
||||
|
|
|
|
|
|
|
|
(2.9) |
|
|
|
|
|
|
|||
|
|
|
|
|
||||
Ф |
|
dФ |
|
I |
в |
; |
||
|
||||||||
|
|
|
|
|
|
|||
dIв |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Uв Rв Iв wσ p( Ф).
40

dФ
Здесь определяется как тангенс угла наклона касательной
dIв 0
к основной кривой намагничивания в точке установившегося режима
(рис. 2.5, б).
Исключив из (2.9) промежуточные переменные E, Ф и Iв, получим искомое уравнение, связывающее U с Uв:
|
|
(Tв p 1) U kв1 Uв, |
(2.10) |
|||||||||||||
где Tв – постоянная времени цепи возбуждения: |
|
|||||||||||||||
|
|
|
|
|
wσ |
|
|
|
|
|
|
|
|
|||
|
|
Tв |
|
|
dФ |
|
; |
|
|
|
||||||
|
|
|
R |
|
|
|
|
|
||||||||
|
|
|
dI |
в |
|
|
|
|
||||||||
|
|
|
|
|
в |
|
0 |
|
|
|
|
|||||
kв1 – коэффициент передачи генератора по возбуждению: |
|
|||||||||||||||
|
|
|
|
RнС |
|
|
|
|
|
|
|
|
||||
k |
в1 |
|
|
|
|
|
|
|
dФ |
. |
|
|||||
R (R R ) |
|
|
||||||||||||||
|
|
dI |
в |
|
|
|||||||||||
|
|
|
в |
|
a |
|
|
н |
|
|
|
|
0 |
|
||
При этом Tв и kв1 зависят от выбранной точки установившегося режима, в которой осуществляется линеаризация.
Если перейти к относительным единицам, уравнение (2.10) примет вид:
|
|
|
|
|
|
(Tв p 1)u kв2uв, |
(2.11) |
|||
где u |
U |
; |
uв |
Uв |
; |
kв2 |
kв1 |
Uв0 |
. |
|
|
|
|
|
|||||||
|
U0 |
|
Uв0 |
|
|
U0 |
|
|||
В структурной схеме системы, в состав которой входит рассматриваемое звено, последнее должно быть изображено, как показано на рис. 2.6.
Рис. 2.6
Выше при выводе уравнения генератора было принято, что скорость вращения якоря и нагрузка постоянны. Изменение этих
41
