
12. СИНТЕЗ ЛИНЕЙНЫХ САУ
12.1. Задачи синтеза САУ
Основным и практически наиболее важным приложением результатов полученных теорией автоматического регулирования и управления является синтез автоматических систем. Он базируется на тех методах улучшения статических и динамических свойств системы, которые были рассмотрены ранее.
Синтезом системы автоматического регулирования называется определение ее структуры и параметров, обеспечивающих определенное качество регулирования. Структура системы и передаточные функции некоторых звеньев не могут быть выбраны совершенно произвольно. Конструкция чувствительного и исполнительного элементов определяется особенностями объекта; в соответствии с их конструкцией предъявляются определенные требования и к остальным функциональным элементам. Поэтому задача синтеза по существу сводится к выбору так называемых корректирующих устройств, обеспечивающих получение требуемого качества при заданных передаточных функциях остальных элементов, и к определению требуемой величины коэффициента усиления.
Задача синтеза, вообще говоря, не имеет однозначного решения. Это объясняется не только тем, что определенное качество может быть получено разными способами, но и прежде всего тем, что сами по себе требования к качественным показателям не являются строго определенными и выбираются на основе целого ряда более или менее справедливых предположений. Во-первых, та или иная совокупность качественных показателей не может полностью характеризовать поведение системы во всех случаях. Так, например, широко распространенные показатели качества регулирования при единичном ступенчатом воздействии будут достаточно точно характеризовать процессы ликвидации небольших начальных рассогласований; при больших рассогласованиях вследствие нелинейности типа «насыщение» эти показатели не будут соблюдаться. Можно также определить точность системы при определенных предполагаемых воздействиях, но невозможно предугадать величину и форму всех возможных воздействий.
263
Во-вторых, стремление довести показатели качества до определенных величин вступает в противоречие с возрастающей сложностью системы. По этим причинам в процессе синтеза следует рассмотреть несколько вариантов и выбрать наилучший на основании анализа синтезированной системы.
Теорией автоматического управления предложен ряд методов синтеза линейных автоматических систем, которые рассмотрены
внастоящем пособии.
12.2.Синтез параметров САУ по минимуму интегральной оценки
Всистемах автоматического регулирования и управления обычно задается объект регулирования. Если, кроме того, задана структура регулятора и корректирующих средств, то задача синтеза сужается до выбора параметров регулятора и корректирующих средств, исходя из поставленных требований. При этом для выбора параметров САУ могут быть использованы интегральные оценки.
Интегральные оценки применяют для суждения о качестве регулирования. Квадратичная интегральная оценка
|
|
I1 ε2(t)dt |
(12.1) |
0 |
|
дает представление об отклонении переходной характеристики от идеальной (ступенчатой). Улучшенная квадратичная интегральная оценка
|
2 |
|
2 |
2 |
|
(12.2) |
|
I2 [ε |
(t) T |
(t)]dt |
|||||
|
ε |
|
|||||
0 |
|
|
|
|
|
|
показывает отклонение переходной характеристики от экспоненты с постоянной времени T.
Чем меньше значение I1 или I2, тем ближе переходная характеристика соответственно к идеальной или к экспоненте.
С помощью интегральных оценок по их минимуму осуществляют также выбор параметров системы.
Пусть по минимуму квадратичной интегральной оценки Ii требуется выбрать параметр α при известных значениях всех остальных параметров системы. Нужно составить выражение для Ii, в него численные значения известных параметров. Тогда
264

квадратичная интегральная оценка Ii становится функцией одного
параметра α, т. е. Ii Ii( ).
Значение α α0, соответствующее минимуму функции Ii, определяют из уравнения
Ii(α) |
0. |
(12.3) |
|
||
α |
|
|
После этого необходимо проверить, что (12.3) есть действительно условие минимума функции Ii(α). Это верно, если при найденном значении α
|
2I |
(α) |
|
|
|
|
|
i |
|
|
|
0. |
(12.4) |
|
2 |
|
||||
|
α |
|
|
|
|
|
|
|
|
α α0 |
|
|
|
Иногда для указанной проверки удобнее вычислить Ii при |
||||||
найденном значении α, а |
также |
|
при |
двух соседних – |
большем |
|
и меньшем. Последние два значения Ii должны быть больше первого. Изложенное справедливо, если производные Ii(α)/ α
и 2Ii(α)/ α2 существуют при всех допустимых значениях α. Может оказаться, что функция Ii(α) не имеет минимума по α внутри области допустимых значений α. Тогда нужно определить Ii при граничных значениях α (при максимальном и минимальном) и выбрать то из них, которое соответствует меньшему значению Ii.
Можно одновременно выбирать значения двух параметров α и β. В этом случае после подстановки в выражение для Ii численных значений всех известных параметров Ii Ii(α;β). Искомые значения параметров α α0 и β β0 определяют из системы уравнений
Ii(α,β) 0; Ii(α,β) 0,
α β
если эти равенства действительно соответствуют минимуму функции
Ii(α;β) по α и β.
Наиболее сложным этапом расчета является составление выражения для I1 или I2. Удобнее подставить численные значения известных параметров в дифференциальное уравнение (или передаточную функцию) системы и затем составлять выражение для I1или I2.
265

Пример 12.1. Определить квадратичную интегральную оценку
I ε2(t)dt
0
для замкнутой системы с передаточной функцией
1
Ф(p) p3 αp2 βp 1
и найти значения параметров α и β, которые минимизируют I при отработке системой единичного ступенчатого воздействия.
Решение. Передаточная функция замкнутой системы по ошибке
Фε(p) 1 Ф(p) |
|
p(p2 αp βp) |
||||||||||||
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
p3 αp2 βp 1 |
||||||
Изображение по Лапласу для ошибки |
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
p2 αp βp |
|
|
|
|
||
E(p) Фε |
(p) |
|
|
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
p p3 αp2 βp 1 |
||||||||||
Согласно (10.22) получаем следующее выражение для ошибки |
||||||||||||||
|
b2a a (b2 2b b )a a b2a |
a |
||||||||||||
I |
|
2 0 1 |
1 |
|
0 2 0 3 |
0 |
2 3 |
, |
||||||
|
2a0a3(a1a2 a0a3) |
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||
для которого b0 a0 |
1; b1 |
a1 |
α; |
b2 a2 |
β; |
|
a3 1. |
|||||||
По этим значениям находим аналитическое представление интегральной оценки
I(α,β) αβ2 α2 β. 2(αβ 1)
Уравнения для параметров α и β, полученные из условия минимизации интегральной оценки,
|
|
I(α,β) |
|
α2 β 2α |
; |
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
α |
|
|
|||||
|
|
|
2(αβ 1) |
|
|
||||
|
I(α,β) |
|
α2β2 |
2αβ 1 α3 |
0. |
||||
|
|
|
2(αβ 1) |
|
|||||
|
β |
|
|
|
|||||
Из первого условия следует αβ 2, тогда из второго 1 α3 0. |
|||||||||
Следовательно, α0 1; |
β0 2; |
Imin 1,5. |
|
|
|||||
266
12.3. Синтез корректирующих устройств по логарифмическим амплитудно-частотным характеристикам
При синтезе корректирующих устройств исходят из того, что объект регулирования (неизменяемая часть системы) задан, а синтезу структуры и параметров подлежат корректирующие устройства или регулятор (изменяемая часть системы). Для решения задачи в такой постановке весьма эффективными оказываются частотные методы синтеза, использующие логарифмические частотные характеристики САУ.
Метод синтеза корректирующих устройств, разработанный В. В. Солодовниковым, основывается на соответствии между логарифмическими частотными характеристиками разомкнутой системы и ее статическими и динамическими свойствами в замкнутом состоянии. Метод используется для САУ минимальнофазового типа, у которых все нули и полюсы передаточной функции разомкнутой системы расположены в левой полуплоскости и амплитудная характеристика однозначно определяет вид фазовой характеристики. Поэтому при синтезе достаточно рассматривать лишь логарифмическую амплитудно-частотную характеристику разомкнутой системы.
Синтез корректирующих устройств методом ЛАХ заключается в следующем. Если исходная передаточная функция разомкнутой
системы – Wисх(p), желаемая передаточная функция – |
Wжел(p) |
|||
и передаточная функция |
последовательного корректирующего |
|||
звена – Wпос(p), то можно записать равенство |
|
|||
W(p) Wисх(p)Wпос(p) Wжел(p), |
(12.6) |
|||
откуда |
|
Wжел(p) |
|
|
W |
(p) |
. |
|
|
|
|
|||
пос |
Wисх(p) |
|
||
|
|
|||
Тогда для ЛАХ можно получить следующее соотношение: |
|
|||
Lпос(ω) Lжел(ω) Lисх(ω). |
(12.7) |
|||
Таким образом, ЛАХ последовательного корректирующего звена получается простым вычитанием ординат исходной ЛАХ из ординат желаемой ЛАХ.
По виду ЛАХ Lпос(ω) определяется структура и параметры последовательного корректирующего устройства. Если коррекция
267
динамических свойств САУ осуществляется параллельным корректирующим устройством или с помощью дополнительной обратной связи, то могут быть использованы формулы пересчета.
Обычно синтез корректирующих устройств САУ можно считать состоящим из пяти этапов: 1) построения ЛАХ исходной
нескорректированной |
системы; 2) |
построения |
желаемой ЛАХ; |
||
3) |
определения вида и параметров корректирующих |
устройств; |
|||
4) |
технической |
реализации |
корректирующих |
устройств; |
|
5) |
поверочного расчета (моделирования) системы с построением |
||||
переходного процесса. |
|
|
|
|
|
|
Рассмотрим некоторые общие рекомендации по формированию |
||||
желаемой ЛАХ. |
|
|
|
Lжел(ω) |
|
|
Желаемой называют асимптотическую |
ЛАХ |
|||
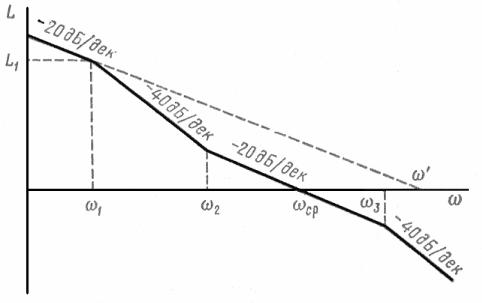
разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Желаемая ЛАХ (рис. 12.1) состоит из трех основных асимптот: низкочастотной, средне-частотной и высокочастотной. Кроме того, могут быть сопрягающие асимптоты, которые соединяют основные.
Рис. 12.1
Строится желаемая логарифмическая амплитудно-частотная характеристика на основании требований к системе. Вид низкочастотной области ЛАХ разомкнутой системы определяет главным образом статические свойства, т. е. точность системы.
268
Среднечастотная область ЛАХ, прилегающая к частоте среза ωс определяет в основном запас устойчивости и качество переходных процессов. Высокочастотная область лишь незначительно влияет на качество процессов управления.
Желаемая ЛАХ в возможно большем интервале частот должна совпадать с ЛАХ исходной нескорректированной системы. В противном случае реализация корректирующих устройств резко усложняется, особенно если требуется увеличить частоту среза и значительно повысить коэффициент усиления в области высоких частот.
В низкочастотной области наклон желаемой ЛАХ должен составлять 20υ дБ/дек, где υ – порядок астатизма системы. Желамая ЛАХ на частоте ω 1 имеет ординату 20lgk, где k 1/C1 – общий коэффициент усиления разомкнутой системы.
В районе частоты среза ωс |
наклон желаемой ЛАХ выбирается |
равным 20υ дБ/дек, что |
позволяет обычно обеспечить |
необходимый запас устойчивости. Чем больше протяженность участка с наклоном 20υ дБ/дек, тем больше запас устойчивости и выше качество переходного процесса.
|
Частоту среза ωс |
желаемой характеристики Lжел(ω) выбирают |
|||||||||||||
из условия |
|
|
|
|
|
ωс α /tр , |
|
|
|
|
(12.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
где α α(σм) (табл. 12.1). |
|
|
|
|
|
|
|
Таблица 12.1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
σм, % |
|
10 |
|
|
20 |
|
|
30 |
|
40 |
|
|
||
|
α |
|
|
0,914 |
|
|
2,625 |
|
|
3,875 |
|
5,066 |
|
||
|
Среднечастотная часть желаемой характеристики Lжел(ω) |
||||||||||||||
пересекает |
ось |
частот |
при |
ω ωс |
с |
наклоном |
20υ дБ/дек |
||||||||
в интервале |
частот [ω2,ω3]. |
При этом |
ω3 (2 4)ωс, ω2 |
ωс2 /ω3, |
|||||||||||
избыток фазы π | (ω2)| |
на левом конце и избыток фазы | (ω3)| π |
||||||||||||||
на правом конце интервала должен быть не менее 40°. |
|
Lжел(ω) |
|||||||||||||
|
Сопряжение |
среднечастотной части |
характеристики |
||||||||||||
с ее низкочастотной |
частью |
выполняется в интервале |
[ω1,ω2] |
||||||||||||
269
прямыми с наклоном –40 или –60 дБ/дек. Сопряжение среднечастотной части Lжел(ω) с ее высокочастотной частью выполняется на интервале [ω3,ω4] ω4 (6 8)ωс прямыми с наклоном –40 дБ/дек. При сопряжении среднечастотной части характеристики следует контролировать, чтобы избыток фазы на концах интервала был не меньше 40 .
Высокочастотная асимптота желаемой ЛАХ мало влияет на свойства системы, поэтому ее следует выбирать так, чтобы корректирующее устройство было возможно более простым. Это достигается при совмещении высокочастотных асимптот характеристик Lжел(ω) и Lисх(ω). Если совмещение не удается, то высокочастотная асимптота Lжел(ω) должна иметь тот же наклон, что и высокочастотная асимптота Lисх(ω).
Желаемая передаточная функция Wжел(p), соответствующая ЛАХ Lжел(ω), приведенной на рис. 12.1, имеет следующий вид:
Wжел(p) |
kжел(T2 p 1) |
|
|
|
, |
(12.8) |
|
|
|||
|
p(T1p 1)(T3p 1)(T4 p 1) |
|
|
где Ti 1/ωi .
Искомая передаточная функция корректирующего звена пассивного или активного четырехполюсника находится по частотным характеристикам Lпос(ω).
Пример 12.2. Используя последовательную коррекцию, выполнить синтез замкнутой системы, у которой прямой тракт имеет передаточную функцию
Wисх(p) |
200 |
, |
|
p(0,1p 1)(0,02p 1)(0,005p 1) |
|||
|
|
так, чтобы переходный процесс отработки входного ступенчатого сигнала имел перерегулирование не более 30 % и время регулирования не более 0,8 с.
Решение. На рис. 12.2 приведены логарифмические частотные характеристики Lисх(ω), исх(ω) прямого тракта системы.
270
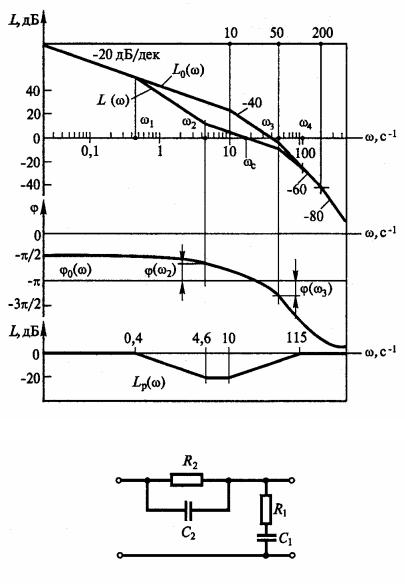
а
б
Рис. 12.2
1. Для построения желаемой логарифмической амплитудночастотной характеристики определим частоту среза
ω3,875 /0,8 15,2с 1.
2.Среднечастотный интервал [ω2,ω3] желаемой характеристики
такой, что ω2 (3,8 7,7) с 1, ω3 (30 60) с 1. Избыток фазы π | жел(ω2)|, определяемый по рис. 12.2, на левом конце интервала составляет (80…63)°, а на правом (30…58)°, поэтому правая граница интервала должна быть изменена: ω3 (45 60) с 1.
271
3. |
Сопряжения |
низкочастотной |
и высокочастотной частей |
||
характеристики выполним так, что ω |
0,4с 1 и ω |
4 |
115с 1. |
||
4. |
Определим |
1 |
частотную |
характеристику |
|
амплитудную |
|
||||
корректирующего звена, вид которой (рис. 12.2, а) позволяет найти передаточную функцию и схему (рис. 12.2, б) этого звена:
|
|
W (p) |
(T1p 1)(T2 p 1) |
, |
|||
|
|
|
|||||
|
|
пос |
|
|
(T3p 1)(T4 p 1) |
||
где |
|
|
|
|
|||
|
|
|
|
|
|
|
|
T1 R1C1, |
T2 R2C2, |
T3 T4 T1(1 R2 / R1)C1 T2. |
|||||
5. Последние соотношения могут быть использованы для |
|||||||
определения четырех параметров звена. Положим C 0,5 мкФ, тогда |
|||||||
остальные параметры определяются однозначно: |
|||||||
T1 1/4,6с; |
T2 1/10с; |
|
T3 1/0,4с; |
T4 1/115с, поэтому |
|||
R1 435 кОм; |
R2 |
2,0 МОм; |
C2 0,05 мкФ. |
|
|
||
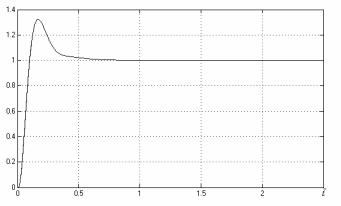
Полученный в результате синтеза переходный процесс, представленный на рис. 12.3, соответствует поставленным требованиям.
Рис. 12.3. Переходный процесс в синтезированной системе
Пример 12.3. Дана нескорректированная система автоматического регулирования с передаточной функцией
Wисх(p) |
2 |
. |
|
p(0.25p 1)(0.0625p 1) |
|||
|
|
Необходимо увеличить коэффициент усиления разомкнутой системы в 20 раз (26 дБ), не нарушая существенно качества
272
