
Тогда
H(p)R(p) [E H(p)R(p)]Φ (p) Φ (p) H(p)R(p)Φ (p).
Полученное выражение преобразуем
H(p)R(p) H(p)R(p)Φ (p) H(p)R(p)[E Φ (p)] Φ (p).
Окончательно получаем
R(p) H(p) |
1 |
Φ |
|
(p)[E Φ |
|
|
1 |
|
|
(12.21) |
|
|
|
(p)] |
R |
(p)R (p). |
|||||
Из (12.21) видно, что регулятор в общем случае может |
||||||||||
выполнять две функции: компенсировать свойства объекта |
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
(12.22) |
|
|
|
|
R (p) H(p) |
|
|
|
|||
и обеспечивать необходимый |
вид |
|
переходных |
процессов |
||||||
в соответствии с Ф (p)
|
|
|
(p)] |
1 |
. |
(12.23) |
R |
(p) Φ |
(p)[E Φ |
|
Элементы матрицы требуемых передаточных функций Φ (p) выбираются исходя из требований к качеству переходных процессов различных параметров объекта. Если ставится задача синтеза многосвязной системы регулирования при условии полной
автономности контуров регулирования, то в матрице Ф (p) следует принять Фij (p) 0приi j.
Пример 12.4. Рассмотрим синтез структуры и параметров МСАУ ГТД с регулируемым соплом, представляющего собой многомерный объект регулирования (рис. 12.9). Здесь управляемыми
могут быть следующие параметры: n – частота вращения вала; Tт – температура газа перед или за турбиной. Управляющие воздействия: Gт – расход топлива в камеру сгорания; Fс – выходное сечение реактивного сопла.
283
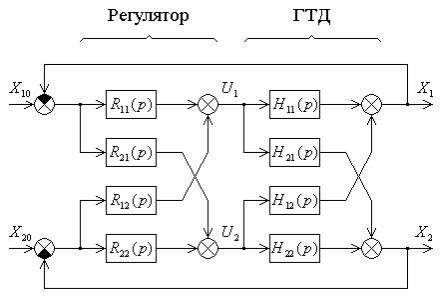
Рис. 12.9
Для ГТД с координатами
|
|
|
|
|
|
n |
|
|
|
|
T |
|
|
|
|
|
G |
т |
|
|
|
|
F |
|
|
|
|
||||
|
X |
1 |
|
|
; X |
2 |
|
|
т |
;U |
1 |
|
|
|
;U |
2 |
|
|
с |
|
|
|
|
|
|||||||
|
n0 |
T |
|
|
|
|
Fс0 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Gт0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
матрица H(p) записывается в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
H(p) |
H11(p) |
H12(p) |
|
|
|
1 |
|
|
|
|
|
k11 |
|
|
k12 |
, |
|||||||||||||||
H |
|
|
(p) |
H |
|
|
(p) |
|
|
|
k |
|
(T p 1) |
k |
|
|
|||||||||||||||
21 |
22 |
(τ |
0 |
p 1) |
|
21 |
|
||||||||||||||||||||||||
где kij,Tij – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
22 |
|
||||||||||
коэффициенты |
|
числителей |
передаточных |
функций |
|||||||||||||||||||||||||||
объекта; τ0 – постоянная времени двигателя, определяемая инерционностью вала турбокомпрессора.
Матрица регуляторов
R11(p) |
R12(p) |
|
R(p) R (p) |
R (p) . |
|
21 |
22 |
|
Тогда матрица передаточных функций системы может быть записана в виде
Φ(p) |
1 |
11(p) |
12(p) |
, |
|
|
|
||
|
||||
|
(E HR) 21(p) |
22(p) |
|
|
где
2 |
|
Фij(p) Hik (p)Rkj(p), |
i j; |
k 1 |
|
284 |
|
2 |
|
Фij(p) Hik (p)Rki(p) H R, |
i, j 1,2; |
k 1 |
|
2 |
|
(E HR) |E HR| 1 Hij(p)Rji(p) H R;
i, j 1
H и R – соответственно определители передаточных матриц H(p)
иR(p).
Вразвернутом виде для диагональной матрицы регулятора получаем следующее выражение
Φ(p) |
1 |
|
|
1 H11(p)R11(p) H22(p)R22(p) H R |
|||
|
|
H11(p)R11(p) H R |
|
|
H12(p)R22(p) |
|
|
||||
|
H |
21 |
(p)R (p) |
H |
22 |
(p)R (p) |
H |
|
. |
|
|
11 |
|
22 |
|
R |
|||
Определитель матрицы Ф(p) при этом равен |
|
|
|
||||||
Φ |
|
|
H R |
|
|
|
. |
||
|
1 H (p)R (p) H |
22 |
(p)R (p) |
H |
|
|
|||
|
11 |
11 |
22 |
|
R |
||||
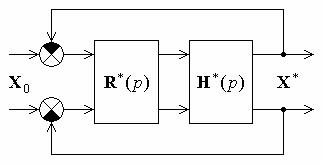
Выбор матрицы Ф (p) требуемых передаточных функций осуществляется путем построения гипотетической МСАУ с тем же количеством регулируемых величин, что и в синтезируемой системе (рис. 12.10), но с минимизацией порядков передаточных функций объекта и регуляторов.
Рис. 12.10
При синтезе двумерной САУ (m 2) передаточные матрицы объекта H (p) и регуляторов R (p) гипотетической системы могут быть выбраны в виде
285
H (p) [H |
|
] |
; R (p) |
1 |
E[R |
] |
, |
ij |
|
||||||
|
(2 2) |
|
τ p ij |
(2 2) |
|
||
где Hij; Rij – вещественные числа, значения которых находятся из
условия задания необходимого качества процессов управления; τ – коэффициент, необходимый для задания движения в системе в безразмерном масштабе времени.
Гипотетическая МСАУ имеет 2m2 8 степеней свободы для придания желаемого вида переходным процессам в системе. Матрица регуляторов в диагональных элементах имеет оператор 1/τp, что обеспечивает свойства астатизма по отношению к ступенчатым воздействиям. Изменяя структуру матриц H (p) и R (p), можно придавать необходимый вид матрице требуемых передаточных функций. Примем Rij 1 при i j и Rij 0 при i j. Тогда для m 2 получим
|
H |
|
H |
|
|
|
1 1 |
0 |
|
H (p) |
11 |
|
12 |
; |
R |
|
|
; |
|
|
H |
|
|
||||||
|
H |
21 |
22 |
|
|
p 0 |
1 |
||
|
|
|
|
|
|
1 |
|
|
|
|
|
H |
τp |
|
|
|
H |
|
τp |
|||
Φ*(p) |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
H |
|
|
|
|
12 |
|
|
. |
|
τ |
2 p |
2 (H |
|
H |
|
)τp |
|
|
H τp |
|
H |
τp |
|
||||||||
|
|
H |
|
|
|
H |
|
|||||||||||||||
|
|
|
|
|
11 |
|
22 |
|
|
|
|
21 |
|
|
|
22 |
|
|
|
|
||
При наложении условий полной автономности контуров |
||||||||||||||||||||||
регулирования в матрице H (p) следует принять |
Hij 0 |
при i j, |
||||||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
H |
τp |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
Φ*(p) |
|
|
|
|
|
|
|
|
|
|
|
11 |
H |
|
|
|
|
|
|
|
. |
|
τ |
2p |
2 (H |
|
H |
|
)τp |
|
|
|
0 |
|
H |
τp |
|
||||||||
|
|
H |
|
|
|
H |
|
|||||||||||||||
|
|
|
|
|
11 |
|
22 |
|
|
|
|
|
|
|
|
22 |
|
|
|
|
||
Определитель матрицы Ф (p) равен
Φ |
|
|
H |
|
|
|
|
. |
τ |
2p2 (H |
H |
|
)τp |
H |
|
||
|
|
11 |
|
22 |
|
|
|
Таким образом, придавая матрице H (p) соответствующий вид,
получаем необходимую структуру матрицы Ф (p)
Тогда, используя (12.21) применительно к двухмерной САУ, получим
286
|
|
1 |
|
H |
|
(p)[ * |
(p) |
|
|
* |
] H |
|
(p) * |
(p) |
R(p) |
|
|
|
|
22 |
11 |
|
Φ |
|
|
12 |
21 |
|
|
H |
|
|
|
|
|
|
* ] H11(p) *21(p) |
|||||||
|
* |
) |
H21(p)[ 11* (p) |
Φ |
||||||||||
|
|
(E Φ |
|
|
|
|
|
|
|
|
|
|||
H |
22 |
(p) * |
(p) H (p)[ * (p) |
|
|
* ] |
|||||||||||
|
|
|
12 |
|
|
|
|
12 |
|
22 |
Φ |
|
, |
||||
H (p) * (p) H (p)[ * (p) * |
] |
||||||||||||||||
|
21 |
|
12 |
|
|
|
|
21 |
|
22 |
|
Φ |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
где ij(p) – элементы матрицы Ф (p); |
|
|
|
|
|
||||||||||||
|
|
|
|
* |
) |
|
Φ |
* |
|
(Ф |
Ф ) 1. |
|
|
|
|||
|
|
|
(E Φ |
|
|
|
|
11 |
22 |
|
|
|
|
||||
Матрица регуляторов может быть приведена к типовому виду |
|||||||||||||||||
|
|
|
|
1 |
kR |
|
|
|
kR |
|
|
|
|
||||
R(p) |
|
|
|
|
11 |
|
|
12 |
|
|
|
. |
|||||
|
|
|
|
|
|
|
kR22 (TR22 p |
|
|
|
|||||||
|
|
|
|
τ p kR21 (TR21 p 1) |
1) |
||||||||||||
Как видно из полученного выражения, система управления является астатической, два регулятора содержат форсирующие звенья. Следовательно, результатом матричного синтеза явились регуляторы с интегральным и пропорционально-интегральным законами управления, не представляющие трудности для технической реализации.
Контрольные вопросы
1.Как определяются неизвестные параметры системы управления с помощью интегральных оценок?
2.Что такое желаемая ЛАЧХ, как она определяется и из каких асимптот она состоит?
3.Какой наклон имеет низкочастотная часть желаемой ЛАЧХ?
4.Какой наклон имеет среднечастотная часть желаемой ЛАЧХ?
5.Какой наклон имеет высокочастотная часть желаемой ЛАЧХ?
6.На какой частоте желаемая ЛАЧХ должна пересекать частотную ось?
7.Как рассчитывается частота среза системы управления?
8.По какой формуле рассчитывается ЛАЧХ последовательного корректирующего звена?
9.Как по виду ЛАЧХ определяется передаточная функция корректирующего звена?
10.Как проводится синтез систем с помощью метода приближения передаточных функций?
287
