
4.МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
4.1.Общая характеристика метода гармонической линеаризации
Широкое распространение для исследования нелинейных систем автоматического управления высокого порядка ( n 2) получил приближенный метод гармонической линеаризации (или гармонического баланса) с применением частотных представлений, развитых в теории линейных систем. Метод гармонической линеаризации, основанный на работах Н. Крылова и Н. Боголюбова, был предложен Л. Гольдфарбом в 1940 г. и применен им для анализа систем автоматического управления. Значительно позже к различным модификациям этого метода пришли ученые многих стран: Тастин в Англии, Оппельт в ФРГ, Дютиль во Франции и Кохенбургер в США. В СССР этот метод получил развитие и обоснование во многих последующих работах. Здесь следует указать работы Е. Попова, И. Пальтова, Я. Цыпкина, М. Айзермана, И. Смирновой, Ю. Топчеева и многих других.
Метод гармонической линеаризации – это метод исследования автоколебаний. Он позволяет определить условия существования и параметры возможных автоколебаний в нелинейных системах. Другие названия этого метода и его модификаций – метод гармонического баланса, метод описывающих функций, метод эквивалентной линеаризации.
Рассмотрим нелинейную систему, схема которой представлена на рис. 4.1. Система состоит из линейной части ЛЧ с передаточной
функцией Wл ( p) |
и нелинейного звена |
НЗ |
с |
конкретно заданной |
характеристикой |
Z = Z ( X ) . Полагаем, |
что |
в |
системе существуют |
автоколебания, амплитуду и частоту которых мы хотим найти. В
рассматриваемом режиме входная величина |
X |
нелинейного звена и |
|
|
выходная Z являются периодическими функциями времени.
Метод гармонической линеаризации основан на предположении, что колебания на входе нелинейного звена являются
синусоидальными, т. е. |
|
X (t) = X 0 + X m sin ωt , |
(4.1) |
81

где |
X m |
– амплитуда и |
ω |
– частота этих автоколебаний, а |
возможная в общем случае постоянная составляющая, автоколебания несимметричны.
Рис. 4.1. Нелинейная система
X 0 |
– |
когда
При этом сигнал на выходе нелинейного звена Z (t) = Z[ X (t)] содержит спектр гармонических составляющих с амплитудами Zm1, Zm2 , Zm3 и т. д. и частотами ω , 2ω , 3ω и т. д. Предполагается, что этот сигнал z(t) , проходя через линейную часть W ( p) , фильтруется
ею в такой степени, что в сигнале на выходе линейной части |
Y (t) |
||
можно пренебречь всеми высшими гармониками |
Ym2 , Ym3 |
и т. д. и |
|
считать, что |
|
|
|
Y (t) Y0 +Ym1 sin(ωt + ) . |
|
|
(4.2) |
4.2. Сущность гипотезы фильтра в методе гармонической линеаризации
Предположение (4.2) носит название гипотезы фильтра, и выполнение этой гипотезы является необходимым условием гармонической линеаризации.
Рис. 4.2. Эквивалентная нелинейная разомкнутая система
Рассмотрим схемы представленные на рис. 4.1 и рис. 4.2. Условие эквивалентности схем, изображенных на этих рисунках, при X 0 = 0 можно сформулировать в виде равенства:
82

X (t) + Y (t)
=
0
.
(4.3)
При выполнении гипотезы фильтра уравнение (4.2) распадается на два других уравнения:
X |
m |
= |
|
|
=
Ym1
π .
,
(4.4)
(4.5)
Уравнения (4.4) и (4.5) носят название уравнений гармонического баланса; первое из них выражает баланс амплитуд, а второе – баланс фаз гармонических колебаний. Таким образом, для того чтобы в рассматриваемой системе существовали незатухающие гармонические колебания, при соблюдении гипотезы фильтра должны выполняться условия (4.4) и (4.5).
Для суждения о выполнении гипотезы фильтра рассмотрим частотные спектры сигналов X (t) , Z (t) и Y (t) в разомкнутой схеме
(рис. 4.2). При моногармоническом сигнале
X (t)
спектры сигналов
Z (t)
и
Y (t)
кроме основной гармоники
Zm1
и Ym1
содержат высшие
гармонические составляющие
Zm
и |
Ym |
.
В зависимости от вида
нелинейности
Z ( X )
амплитуды высших гармоник в сигнале
Z (t)
будут большими или меньшими.
Автоколебания в нелинейных системах всегда несинусоидальны вследствие искажения их формы нелинейным звеном. Поэтому метод гармонической линеаризации является принципиально приближенным и область его применения ограничена случаями, когда автоколебания на входе нелинейного звена достаточно близки к синусоидальным. Для того чтобы это имело место, линейная часть системы должна не пропускать высшие гармоники автоколебаний, т.е. являться фильтром низких частот.
Из вышесказанного следует, что удельный вес высших гармоник в сигнале Y (t) меньше, чем в сигнале Z (t) . Справедливости гипотезы
фильтра соответствует такая характеристика линейной части
W |
( |
л |
|
jω)
,
чтобы, проходя через нее, все гармоники, кроме первой, затухали до пренебрежимо малых значений.
Количественно это условие можно выразить следующим образом:
Z mk |
|
Wл ( jkω) |
1, |
(4.6) |
|
Z m1 |
Wл ( jω) |
||||
|
|
|
где k – номер рассматриваемой гармоники.
83
В общем случае условие (4.6) должно выполняться для любого
целого значения |
k 2. В |
том случае, когда рассматриваются |
||
симметричные колебания, в |
сигнале |
Y (t) |
отсутствуют четные |
|
гармоники и условие (4.6) должно рассматриваться при k 3.
С помощью метода гармонической линеаризации решаются две
основные группы задач: |
|
|
|
а) исследование |
моногармонических |
автоколебаний |
в |
нелинейных замкнутых системах, (условие (4.6) должно выполняться для частоты ω предполагаемых автоколебаний);
б) исследование условий отсутствия моногармонических автоколебаний в нелинейных замкнутых системах, (условие (4.6)
должно выполняться во всем диапазоне частот |
0 ω |
предполагаемых автоколебаний). |
|
Так как обычно Zmk / Zm1 1 при k 2, то для приближенных
расчетов условие (4.6) может быть смягчено и сформулировано так: наклон логарифмической частотной характеристики линейной части должен быть, по крайней мере – 20 40 дБ/дек.
При наклоне характеристик − 20 дБ/дек
W |
( j2ω) |
|
1 |
|
л |
|
|
= |
|
W |
|
( jω) |
2 |
|
|
|
|||
л |
|
|
|
|
а при наклоне характеристик − 40
W |
( j2ω) |
|
1 |
|
л |
|
|
= |
|
W |
|
( jω) |
4 |
|
|
|
|||
л |
|
|
|
|
|
W |
( j3ω) |
|
и |
л |
|
|
W |
|
( jω) |
|
|
|
||
|
л |
|
|
дБ/дек |
|||
|
W |
( j3ω) |
|
и |
л |
|
|
W |
|
( jω) |
|
|
|
||
|
л |
|
|
 =
=
 =
=
1 3
1 9
;
.
Исследования автоколебаний несколько различаются в зависимости от симметрии или несимметрии рассматриваемых колебаний. При исследовании несимметричных автоколебаний большое значение имеет постоянная составляющая сигнала в системе. При нечетном характере нелинейностей и отсутствии внешнего воздействия (U (t) = 0 на рис. 4.1) наибольший интерес
представляют симметричные автоколебания.
Выполнение гипотезы фильтра в форме сильного неравенства (4.6) встречается в практических задачах сравнительно редко, поэтому применение гармонической линеаризации бывает строго обосновано далеко не всегда. Однако даже при отсутствии строгого обоснования этот метод во многих практических задачах наиболее прост и дает удовлетворительное приближенное представление о процессах, протекающих в реальных устройствах. При этом в каждом
84
случае невыполнения гипотезы фильтра полученное решение нуждается в экспериментальном или теоретическом подтверждении на математической или физической модели.
4.3. Коэффициенты гармонической линеаризации нелинейных звеньев
Поскольку мы считаем, что линейная часть системы пропускает только основную гармонику автоколебаний, имеет смысл интересоваться только этой гармоникой на выходе нелинейного звена. Поэтому разложим выходные колебания в ряд Фурье и отбросим высшие гармоники. В результате получим:
Z (t) = Z ( X ) = Z0 + C1 sin ωt + C2 cosωt . |
(4.7) |
Здесь
|
|
1 |
|
2π |
|
|
|||
|
|
|
|
|
|
|
|
||
Z0 |
= |
2π |
|
Z ( X )d (ωt); |
|||||
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
1 |
|
2π |
|
|
|
||
|
= |
|
|
Z ( X ) sin ωtd (ωt); |
|||||
|
|
||||||||
1 |
|
|
|||||||
C |
π |
|
|
|
|||||
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
1 |
2π |
|
|
|||||
|
|
|
|
||||||
= |
|
Z ( X )cosωtd (ωt); |
|||||||
C2 |
|
|
|
||||||
|
|
π |
|
0 |
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
X |
= X |
0 |
+ X |
m |
sin ωt. |
||||
|
|
|
|
|
|
|
|||
(4.8)
Перепишем выражение (4.7) в более удобном для последующего использования виде, подставив в него получающиеся из (4.1)
следующие выражения для sin ωt |
и cos ωt : |
|
|
|
|
|
||||||||||||||||
|
sin ωt = |
X − X 0 |
; |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X m |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.9) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
p( X − X 0 ) |
|
|
|
|
|
||||||
|
cosωt = |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X m ω |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставив эти выражения в (4.7), будем иметь: |
|
|||||||||||||||||||||
Z = Z |
0 |
+ (k |
г |
+ |
k'г |
p)( X − X |
0 |
) |
|
|
(4.10) |
|||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z = k |
г0 |
X |
0 |
+ (k |
г |
+ |
k'г |
p)( X − X |
0 |
) . |
(4.11) |
|||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
ω |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
85
Здесь введены обозначения:
|
k |
|
= |
Z |
0 |
; |
||
|
г0 |
|
|
|||||
X |
|
|||||||
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
C |
|
|
|
k |
г = |
|
|
1 |
; |
|||
X |
|
|
||||||
|
|
|
|
m |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
C |
|
|
|
k |
'г |
= |
|
|
2 |
. |
||
|
X m |
|||||||
|
|
|
|
|
|
|||
(4.12)
Дифференциальное уравнение (4.11) справедливо для синусоидального входного сигнала (4.1) и определяет выходной сигнал нелинейного звена без учета высших гармоник.
а
б
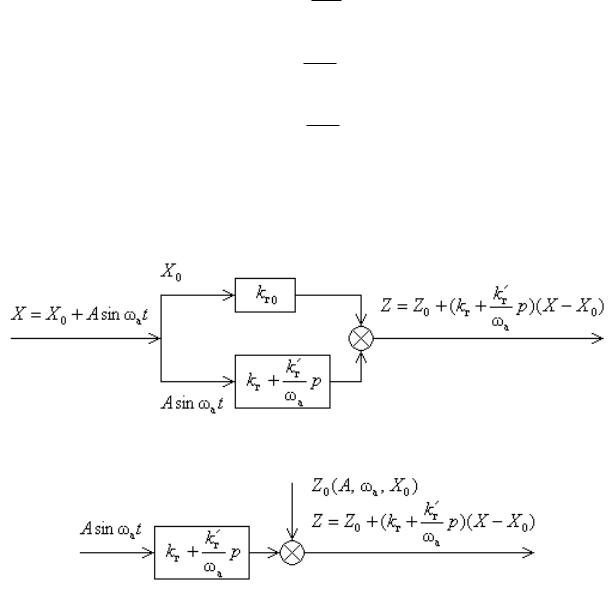
Рис. 4.3. Эквивалентное линейное звено, полученное в результате гармонической линеаризации
Коэффициенты
kг0 ,
kг
и
kг
в соответствии с выражениями (4.8)
для коэффициентов Фурье составляющей X 0 , амплитуды
являются функциями постоянной X m и частоты ω автоколебаний на
входе нелинейного звена. При фиксированных X m , ω и
X 0
уравнение (4.11) является линейным. Таким образом, если отбросить высшие гармоники, то для фиксированного гармонического сигнала исходное нелинейное звено может быть заменено эквивалентным
86
линейным, описываемым уравнением (4.11). Эта замена и называется гармонической линеаризацией.
На рис. 4.3, а условно изображена схема этого звена, состоящая из двух параллельных звеньев. Одно звено kг0 пропускает
постоянную составляющую, а составляющую автоколебаний.
Коэффициенты |
kг0 |
, |
kг |
и
другое – только
|
называются |
kг |
синусоидальную
коэффициентами
гармонической линеаризации или гармоническими коэффициентами передачи: kг0 – коэффициент передачи постоянной составляющей, а
kг и kг – два коэффициента передачи синусоидальной составляющей
автоколебаний. Эти |
коэффициенты определяются нелинейностью |
||
Z ( X ) и значениями |
X m = A, ω и X 0 по формулам (4.8). Для всех |
||
безынерционных нелинейных звеньев величины kг0 , |
kг |
|
|
и kг не |
|||
зависят от ω и являются функциями только амплитуды |
X m |
и X 0 . |
|
Постоянная составляющая Z0 на выходе нелинейного звена [см.
уравнения (4.7) и (4.10)] появляется по одной из двух причин:
1) если к системе приложено внешнее постоянное воздействие создающее X 0 [см. уравнение (4.1)];
2) если характеристика, нелинейного звена несимметрична относительно начала координат, вследствие чего происходит явление выпрямления входного синусоидального сигнала.
При гармонической линеаризации нелинейных звеньев с такими
характеристиками нельзя выражать |
Z0 |
через |
X 0 |
с помощью |
коэффициента гармонической линеаризации kг0
|
|
|
Z |
0 |
= k |
г0 |
X |
0 |
|
|
|
|
|
|
|||
так как здесь |
Z0 0 |
, при |
X 0 = 0 . |
Поэтому |
||||
, т. е. в виде
(4.13)
для несимметричных
нелинейностей нельзя пользоваться уравнением (4.11), а следует применять уравнение (4.10). Соответствующая схема представлена на рис. 4.3, б.
При отсутствии внешнего воздействия и симметричной характеристике Z ( X ) постоянная составляющая Z0 = 0 и уравнение
(4.11) принимает вид: |
|
|
|
|
|
|
Z = (k |
г |
+ |
k'г |
p) X |
(4.14) |
|
ω |
||||||
|
|
|
|
|||
|
|
|
|
|
или
87

|
|
|
|
Z = Wн ( p) X |
, |
|
|
|
k' |
|
|
|
|
где |
Wн = kг + |
г |
p |
– передаточная |
функция |
|
ω |
||||||
|
|
|
|
|
линейного звена, которую можно назвать передаточной функцией нелинейного звена.
В соответствии с (4.11) и (4.12) коэффициент
(4.15)
эквивалентного
гармонической
kг |
определяем |
выходную гармоническую составляющую, совпадающую по фазе с
входным гармоническим сигналом, а коэффициент |
|
– выходную |
kг |
составляющую, сдвинутую по фазе относительно входного сигнала
|
|
|
на / 2 вперед или назад в зависимости от знака kг , то есть знака C2 . |
||
Коэффициент |
|
появляется в уравнении (4.11) в случае |
kг |
||
неоднозначных характеристик
Z ( X
)
.
Неоднозначность характеристики приводит к тому, что при изменении знака входного сигнала происходит запаздывание в изменении выходного сигнала в связи с переходом на другую ветвь характеристики Z ( X ) . В результате при гармоническом входном
воздействии возникает запаздывание по фазе первой гармоники на выходе относительно входного сигнала. Поэтому в данном случае в
выражении (4.7) коэффициент |
C |
2 |
при косинусоидальной |
|
|
|
составляющей не равен отрицательным получится и
нулю и отрицателен. Соответственно
k |
в уравнении (4.11). |
г |
В случае безынерционной однозначной нелинейности первая гармоника на выходе нелинейного звена обязательно совпадает по фазе с входным сигналом. Поэтому уравнение (4.11) принимает вид:
Z = kг0 ( X m , X 0 ) X 0 + kг ( X m , X 0 )( X − X 0 ) . |
(4.16) |
Здесь в функциями X
скобках показано, что величины
m и X 0 .
kг0
и kг являются
При нечетной однозначной характеристике и постоянного внешнего воздействия уравнение (4.16) упрощается:
Z = kг ( X m ) X .
отсутствии
предельно
(4.17)
88
а |
б |
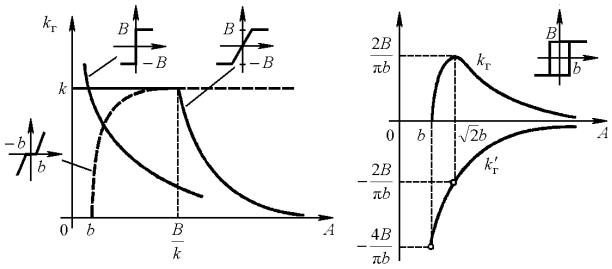
Рис. 4.4. Графики коэффициентов гармонической линеаризации
kг
( X
На |
рис. |
m ) |
и k'г |
4.4,
( X |
m |
) |
|
|
а и б в качестве примера приведены графики для трех нечетных нелинейностей. Эти графики
имеют ясный физический смысл, и их можно получить экспериментально подобно частотным характеристикам. Во всех случаях, когда характеристика нелинейного звена имеет насыщение, коэффициенты гармонической линеаризации стремятся к нулю при X m → , поскольку при этом амплитуда выходного сигнала остается
ограниченной. Если характеристика имеет зону нечувствительности, наоборот, влияние нелинейности падает с ростом X m и коэффициент
kг
стремится к значению коэффициента передачи
k
линейного
участка |
характеристики. |
При |
неоднозначной |
релейной |
|||
характеристике |
влияние |
неоднозначности |
проявляется |
в |
|||
запаздывании по фазе, и соответственно величина коэффициента |
k |
||||||
г |
|||||||
уменьшается по мере увеличения |
X m по сравнению с шириной петли. |
При гармонической линеаризации нелинейное звено заменяется линейным, эквивалентным для постоянной составляющей: входного сигнала и приближенно эквивалентным для его колебательной составляющей. При этом приближенно принимается, что спектр колебательной составляющей входного сигнала состоит из одной гармоники, и пренебрегается ее искажением в нелинейном звене.
89
4.4. Анализ параметров автоколебаний нелинейных систем методом гармонической линеаризации
Рассмотрим замкнутую САУ, изображенную на рис. 4.1. Наша задача – найти параметры возможных автоколебаний в определенной, интересующей нас точке системы.
Первым этапом решения является осуществление гармонической линеаризации и с ее помощью определение параметров возможных автоколебаний на входе нелинейного звена.
Рассмотрим вначале более простой случай, когда отыскиваются автоколебания в виде
X = X m sin ωt , |
(4.18) |
т. е. без постоянной составляющей. имеет нечетную характеристику,
воздействия, |
создающего |
X 0 |
Это будет, если нелинейное звено и нет внешнего постоянного
. Применив гармоническую
линеаризацию, заменим нелинейное звено линейным, описываемым уравнением (4.15):
В результате получим линейную САУ с передаточной функцией
W ( p) =Wл ( p)Wн ( p) . |
(4.19) |
Входящие в |
W |
н |
( p) |
величины |
kг ( X m , ω) |
и |
|
|
|
|
|
как нелинейные функции искомых неизвестных
k' |
г |
( |
|
|
|
X |
|
|
|
m |
|
X
и
m |
, |
|
|
ω |
|
ω)
.
выражаем
Заметим еще раз, что получаемая только при фиксированных величинах
система
X m и ω .
является линейной При их изменении
система по-прежнему нелинейная, так как содержит коэффициенты kг и k 'г , являющиеся функциями этих величин.
Искомые значения параметров
X m
и
ω
,
входящих в
передаточную функцию (4.19) линейной САУ, соответствуют наличию в этой системе незатухающих колебаний, т. е. нахождению ее на границе устойчивости из-за наличия у характеристического уравнения пары сопряженных мнимых корней. Иными словами, значения X m и ω могут быть найдены с помощью известных
критериев устойчивости линейных систем как значения варьируемых параметров, при которых система оказывается на границе устойчивости, соответствующей незатухающим колебаниям.
Таким образом, дело сводится к применению известных методов определения границы устойчивости линейных систем.
90
