
Так, по критерию Гурвица условие наличия у характеристического уравнения мнимых корней сводится к равенству
|
|
n−1 |
= 0 , |
(4.20) |
где |
n −1 |
– предпоследний |
минор |
определителя Гурвица, |
составленного из коэффициентов левой части
D( p)
уравнения
замкнутой системы. Левая часть D( p) , как известно, числителя и знаменателя передаточной функции W ( p) .
По критерию Найквиста то же условие имеет вид:
W ( jω) = −1,
т. е. с учетом (4.19)
равна сумме
(4.21)
Wн ( jω)Wл ( jω) = −1.
(4.22)
Из критерия Михайлова это условие получаем в виде
|
|
|
|
D( jω) = 0 . |
(4.23) |
Выбор того или иного критерия устойчивости для нахождения |
|||||
значений |
X m |
и |
ω |
зависит от конкретной схемы |
системы и |
определяется общими рекомендациями. |
|
||||
В результате находятся параметры возможных автоколебаний в |
|||||
системе, |
например, |
в виде зависимости X m (ω) . Если при синтезе |
|||
САУ требуется исследовать зависимость автоколебаний от какоголибо параметра системы, получаются уже три неизвестных параметра и решение находится в виде зависимостей X m и ω от варьируемого
параметра системы. При двух варьируемых параметрах системы решение получается в виде линий фиксированных значений X m и ω
в плоскости этих параметров.
Нелинейный характер зависимостей входящих в Wн ( p)
коэффициентов
kг
и k 'г гармонической линеаризации от
X m
и ω
делает задачу нахождения искомых значений X m и ω значительно
более сложной, чем в случае определения границ устойчивости линейных систем. Поэтому обычно прибегают к методу последовательных приближений или графическим методам (как и в случае решения аналогичных уравнений при статистической линеаризации).
В частности, при использовании уравнения (4.22) можно рекомендовать следующий графический способ, предложенный Л. С. Гольдфарбом. В комплексной плоскости строятся годограф
91

W |
( |
л |
|
jω)
, то есть АФЧХ линейной части, и годограф
− |
1 |
|
|
W |
( jω) |
н |
|
. При
этом значения
X m
указываются как параметр на текущих точках
последнего годографа. В соответствии с (4.22) точки пересечения годографов определяют искомые значения амплитуды X m и частоты
ω автоколебаний. (Значение X m берется с годографа нелинейного
звена, а находить
ω |
– с годографа |
точку пересечения
линейной части.) Можно, наоборот,
годографов |
|
1 |
и |
−Wн ( jω) , как |
|
|
|||
W |
л |
( jω) |
|
|
|
|
|
|
предложил Коченбургер.
При применении логарифмического критерия условие (4.22) принимает вид:
L |
л |
(ω) + L |
|
(ω) = 0; |
||
|
|
н |
|
|||
|
|
(ω) + |
|
(ω) = −π. |
||
|
л |
н |
||||
|
|
|
||||
устойчивости
(4.24)
В этом случае строится серия ЛАХ и ЛФХ системы для ряда
значений |
X m . Искомыми значениями |
X m |
будут те, при которых |
ЛФХ пересечет уровень − на частоте среза. В свою очередь, частота среза определяет значение частоты ω .
В тех случаях, когда входящие в |
Wн |
коэффициенты |
kг |
и |
k 'г |
достаточно сложно зависят от
X m
и
ω
, так что вычислить
Wн
по
X m
и |
ω |
затруднительно, рекомендуется следующий |
(4.22) или (4.23) находятся сперва зависимости |
k |
г |
|||
|
|
|
|
|
|
берутся зависимости |
kг ( X m , ω) |
и |
k'г ( X m , ω) |
, |
|
способ. На основе (ω) и k 'г (ω) . Затем определяемые по
(4.12), и совместно с первыми
находятся значения |
X m |
и |
зависимостями графическим решением ω удовлетворяющие обеим парам
зависимостей.
Наконец, в наиболее сложных случаях приходится прибегать к методу последовательных приближений. Например, при применении условия (4.23) по критерию Михайлова последовательно задаются рядом значений X m и, строя каждый раз годограф D( jω) ищут
значение X m , при котором годограф пройдет через начало координат.
92
4.5. Анализ устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
После того как найдены возможные автоколебательные режимы, необходимо исследовать их на устойчивость. Реально существовать в системе могут только устойчивые колебания. Для исследования устойчивости осуществляют линеаризацию системы переходом к приращениям относительно рассматриваемого колебательного режима и применяют обычные критерии устойчивости линейных САУ. Существуют также более простые необходимые критерии устойчивости колебаний. Часто вопрос об устойчивости найденного периодического решения оказывается ясным и из чисто физических соображений.
Наконец, как уже отмечалось, необходимо осуществить проверку гипотезы о том, что линейная часть системы в достаточной мере является фильтром нижних частот для найденных значений
частоты ω |
автоколебаний. |
|
|
|
Ранее |
была |
рассмотрена |
система |
автоматического |
регулирования, содержащая нелинейное звено и линейную часть (рис. 4.1), и было отмечено, что условием существования автоколебаний в системе является гармонический баланс колебаний на входе нелинейного звена и на выходе звена сравнения. Воспользовавшись комплексным коэффициентом усиления, можно записать уравнение гармонического баланса как уравнение (4.22).
При этом предполагается, что исследуются симметричные автоколебания при отсутствии постоянной составляющей.
Записанное условие можно рассматривать как уравнение относительно неизвестных частоты и амплитуды автоколебаний (амплитуда определяется на входе нелинейного звена). Это уравнение распадается на два (оно записано для комплексных величин), его действительные решения, если они существуют, дают частоту и амплитуду возможных автоколебаний в системе.
Согласно Л. С. Гольдфарбу уравнение автоколебаний удобно решать графически следующим образом. Запишем уравнение (4.22) в виде
|
1 |
−1 |
~ |
|
|
Wл ( jω) = − |
|
= −Wн |
( A) = Vн ( A) , |
(4.25) |
|
Wн ( A) |
|||||
|
|
|
|
где A = X m – амплитуда автоколебаний.
93
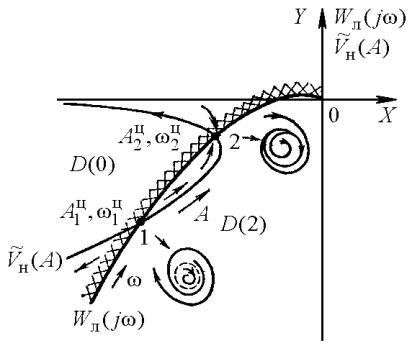
На рис. 4.5 изображены годографы частотной характеристики
линейной части Wл ( jω) |
и инверсного коэффициента гармонической |
||
линеаризации, взятого |
со знаком минус: Vн ( A) = −Wн |
−1 |
( A) . Они |
|
|||
пересекаются в двух точках 1 и 2, определяющих искомые автоколебательные режимы (циклы).
Рис. 4.5. Годографы частотной характеристики линейной части и инверсного коэффициента гармонической линеаризации
Не каждое из найденных решений соответствует устойчивым автоколебаниям, т. е. автоколебаниям, которые в случае вариации, вызванной кратковременным возмущением, восстанавливаются.
Для суждения об устойчивости автоколебаний будем рассматривать близкие к гармоническим колебания
X(t) = Aцeαt sin( ωt + )
счастотой мало отличающейся от частоты автоколебаний.
Затухание или нарастание колебаний характеризуется коэффициентом α : если α 0, то колебания нарастают, если α 0, то
колебания затухают. |
|
|
|
|
Коэффициент |
передачи |
линейной |
части |
вблизи |
автоколебательного |
режима Wл (α + jω) . При |
этом |
| α | ω . В |
|
94
автоколебательном |
режиме |
ω = ω |
ц |
и α |
= 0. |
||
|
|||||||
определяющей автоколебательный режим |
|
||||||
~ |
|
( A) + jY ( A) = W (α + jω) = X |
|||||
V ( A) = X |
н |
||||||
н |
|
н |
л |
|
|
|
|
В окрестности точки,
л (α, ω) + Yл (α, ω) .
Условия устойчивости автоколебаний в точке (
ω |
ц |
|
и Aц ) могут
быть сформулированы так: если |
dα |
0 |
, то колебания устойчивы, |
|
dA |
||||
|
|
|
если, наоборот, dAdα 0 , то они неустойчивы.
Условие устойчивости автоколебаний может быть получено на основании дифференцирования последнего выражения и приравнивания действительных и мнимых частей:
dX н |
|
= |
X л |
|
dα |
|
+ |
|
X л |
|
dω |
|
, |
|
dA |
α |
dA |
|
ω |
|
dA |
||||||||
|
|
|
|
|
|
|
||||||||
dY |
|
Y |
|
dα |
|
Y |
|
dω |
|
|||||
н |
= |
л |
|
|
|
+ |
|
л |
. |
|
||||
dA |
α |
|
|
|
ω |
|
||||||||
|
|
dA |
|
|
|
dA |
|
|||||||
На основании условий Коши – Римана для функций комплексного переменного можно записать
|
X |
л |
= |
Y |
л |
; |
|
|||
|
|
|
|
|
|
|||||
α |
ω |
|
||||||||
|
|
|
||||||||
|
Y |
|
|
|
|
X |
|
|
||
|
л |
= − |
л |
. |
||||||
|
|
|
||||||||
|
|
|
|
ω |
||||||
|
|
|
|
|
|
|||||
α |
|
|
|
|
||||||
(4.26)
(4.27)
аналитических
(4.28)
Тогда, подставляя (4.28) в (4.26) и (4.27) и решая уравнения,
относительно |
dα |
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
dX |
н |
|
X |
л |
|
dY |
|
|
||||
|
|
|
|
л |
|
|
|
|
+ |
|
|
|
н |
|
|
|||
|
|
dα |
|
ω |
dA |
ω |
dA |
|
|
|||||||||
|
|
= |
|
|
|
. |
(4.29) |
|||||||||||
|
|
dA |
|
X |
|
|
|
|
|
|
Y |
|
|
|||||
|
|
|
|
л |
|
|
2 |
|
|
|
2 |
|
|
|||||
|
|
|
( |
|
|
) |
+ ( |
|
л |
) |
|
|
||||||
|
|
|
|
ω |
|
ω |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как знаменатель уравнения (4.29) всегда положителен, то условие устойчивости автоколебаний можно сформулировать следующим образом:
|
Yл |
dXн |
|
+ X л |
dYн |
0 . |
(4.30) |
|
|
|
|||||
|
ω dA |
ω |
dA |
|
|||
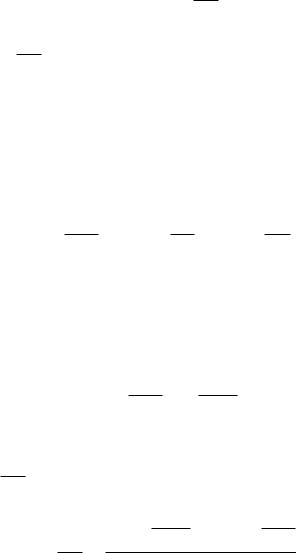
Выражению (4.30) можно дать наглядную геометрическую |
|||||||
интерпретацию |
(рис. 4.6. а, |
если |
рассматривать |
D-разбиение |
|||
плоскости X, |
У кривой |
1, |
описываемой |
уравнением |
|||
95
W |
( jω) = |
л |
|
D(2), где
X л α
(ω) + jY |
(ω) |
л |
|
0. |
|
при 0 ω на областях: D(0), где
а
α
0
, и
б
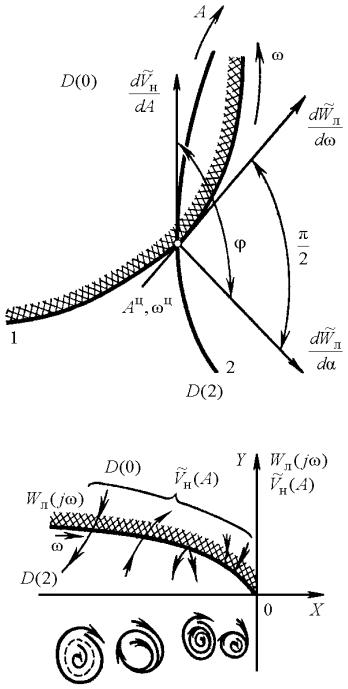
Рис. 4.6: а) – геометрическая интерпретация условия устойчивости автоколебаний; б) – возможные типы автоколебаний и их фазовые портреты
Вектор
Wл = |
X л + j |
Yл |
(4.31) |
ω |
ω |
ω |
|
96

направлен по касательной к этой кривой в сторону возрастания |
ω , а |
согласно (17.28) вектор |
|
dW |
|
X |
л |
|
Y |
|
W |
|
|
л |
= |
|
+ j |
л |
= − j |
л |
(4.32) |
||
dα |
α |
α |
ω |
||||||
|
|
|
|
||||||
направлен нормально к этой кривой в сторону возрастания α , т. е. в область D(0). Рассматривая в точке пересечения частотного (1) и амплитудного (2) годографов вектор dVн / dA , можно определить угол
между векторами dV |
н |
/ dA |
и W / . Условие, когда этот угол по |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
||
модулю лежит в пределах от |
/ 2 |
|
до |
, согласно правилам алгебры |
|||||||||||||||||
комплексных чисел определяется выражением |
|
|
|
|
|
|
|
||||||||||||||
Re |
Wл |
Re |
dVн |
+ Im |
Wл |
Im |
dVн |
= |
X л |
|
|
dX н |
+ |
Yл |
|
dYн |
. (4.33) |
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
α |
|
dA |
|
|
α |
|
dA |
|
α |
|
dA |
α |
|
dA |
||||||
Если учесть условия (4.28), |
|
то выражение (4.33) |
совпадает с |
||||||||||||||||||
неравенством (4.30) и, следовательно, соответствует условию устойчивости автоколебаний.
Точка 1 на рис. 4.5 соответствует неустойчивым колебаниям и неустойчивому предельному циклу в фазовом пространстве, а точка 2
– устойчивым колебаниям и устойчивому предельному циклу.
Возможны случаи односторонне неустойчивых автоколебаний, в |
|
которых случайное возрастание амплитуды нарушает режим, а |
|
уменьшение ее на режиме не сказывается или, наоборот, уменьшение |
|
амплитуды нарушает режим, |
а возрастание ее на режиме не |
сказывается. Такие случаи |
соответствуют точкам касания |
амплитудного |
н |
|
и частотного Wл ( j ) годографов. |
|
|||
|
|
V |
( A) |
|
|
|
|
Все четыре возможных типа автоколебаний и соответствующие |
|||||||
им фазовые портреты показаны на рис. 4.6, б. |
|
|
|||||
На |
основании |
проведенных |
рассуждении |
можно |
|||
сформулировать следующие правила суждения об устойчивости автоколебаний: колебания устойчивы, если, двигаясь по характеристике нелинейного элемента в сторону возрастания амплитуды, переходим из области D(2) в область D(0). Наоборот, автоколебания неустойчивы, если, двигаясь по характеристике нелинейного элемента в сторону возрастания амплитуды, переходим из области D(0) в область D(2). В первом случае / 2 , а во
втором – 0 / 2 .
97
а
б
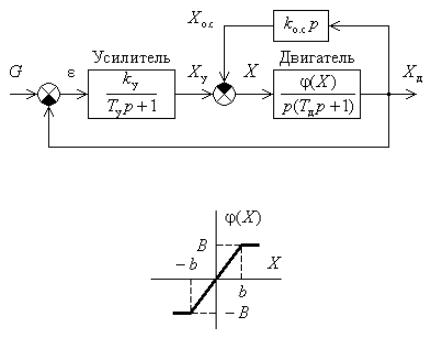
Рис. 4.7. Структурная схема следящей системы
Пример 4.1. Рассмотрим пример применения метода гармонической линеаризации для исследования условий устойчивости и автоколебаний следящей системы, структурная схема которой показана на рис. 4.7, а. Система состоит из двигателя Д с постоянной времени Tд , усилителя У с постоянной времени TУ и
коэффициентом передачи
kУ
и корректирующей гибкой обратной
связи ГОС с коэффициентом передачи системы является угол поворота X д
kо.с.
вала
. Выходной величиной двигателя, а входной
величиной, которая отслеживается системой, – задающее воздействие G . Двигатель представляет собой нелинейное звено вследствие
ограничения скорости вращения |
pX д его вала. Согласно |
схеме, |
|
уравнение двигателя имеет вид: |
|
|
|
(Т д p +1) pX д = ( X ) , |
|
(4.34) |
|
где ( X ) – однозначная нечетная характеристика с насыщением, |
|||
приведенная на рис. 4.7, б. |
|
|
|
Решение. Ограничимся рассмотрением случаем, когда |
G = 0 . |
||
Тогда гармоническая линеаризация нелинейности |
( X ) |
дает |
|
уравнение: |
|
|
|
( X ) = kг ( X m ) X . |
|
(4.35) |
|
98 |
|
|
|

Здесь, коэффициент kг функцией только амплитуды
гармонической линеаризации является X m автоколебаний и равен
где
|
|
k |
|
|
г |
k |
д |
= B / b |
|
|
k |
д |
, при X |
m |
b |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
= 2kд |
|
|
b |
|
b |
|
|
b |
|
|
|||||
(arcsin |
+ |
1 |
+ |
|
), при X |
|
|||||||||
|
|
X |
|
X |
|
|
2 |
m |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
m |
|
|
m |
|
|
X m |
|
|
|
– коэффициент передачи двигателя
b
на
,(4.36)
линейном,
участке его характеристики ( X ) . Соответствующий график характеристики
k |
г |
( X |
m |
) |
|
|
|
для такой
нелинейности показан на рис. 4.4, а. В результате передаточная функция разомкнутой гармонически линеаризованной системы, имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
( p) |
|
|
W ( p) =W |
|
|
( p) |
|
|
|
|
|
|
|
д |
|
|
||||
у |
|
+W |
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
( p)W |
( p) |
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
о.с. |
|
д |
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||
W |
|
( p) = |
|
|
|
|
|
у |
|
; |
|
|
|
|
|||
у |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
T |
|
|
|
p +1 |
|
|
|
|
||||
|
|
|
|
|
|
у |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
( p) = |
|
k |
г |
( X |
m |
) |
; |
|
|||||||
W |
д |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
(T |
|
|
p +1) p |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|||
|
|
|
|
( p) = k |
|
|
p. |
|
|
|
|
||||||
W |
о.с. |
о.с. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
(4.37)
(4.38)
Отсюда левая часть уравнения замкнутой системы, равная сумме числителя и знаменателя W ( p) ,
D( p) = (T |
у |
p +1)(T |
p +1) р +[k |
о.с. |
p(T |
у |
p +1) + k |
У |
]k |
г |
( X |
m |
) |
|
д |
|
|
|
|
|
|
или
(4.39)
D( p)
где
a0a1a2a3
=a0 p3 + a1 p2 + a2 p
=TуTд ;
=Tу (1 + kо.с.kг ( X m ))
=1 + kо.с.kг ( X m );
=kо.с.kг ( X m ).
+ a |
, |
3 |
+ Tд ;
(4.40)
(4.41)
99
При малых отклонениях от установившегося |
|
|||||
соответствующего |
X = 0 , когда |
X b, рассматриваемая |
||||
является линейной. В этом случае в (4.39) надо заменить |
kг |
|||||
kд . Условие устойчивости такой линейной системы, |
|
|||||
критерию Гурвица, имеет вид: |
|
|
|
|
|
|
|
n−1 = a1a2 − a0a3 0 |
1 , |
|
2 , a3 . |
|
|
при положительности всех коэффициентов a0 , |
|
|
||||
|
|
|
a |
a |
|
|
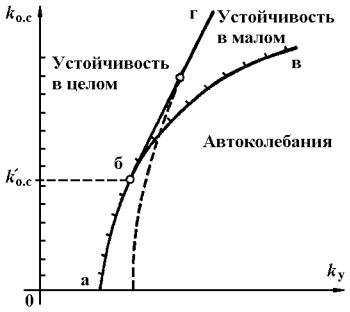
Рис. 4.8. Область устойчивости следящей системы
режима, система
( X m ) на
согласно
(4.42)
На рис. 4.8 построена область устойчивости этой
первом квадранте плоскости коэффициентов |
k у |
и |
kо. |
с
системы в
., которые
приняты в качестве варьируемых параметров системы. Область
устойчивости ограничена слева осью k |
о.с. |
на которой |
a |
3 |
= 0 |
, а справа |
|
|
|
|
|
– параболой абв, уравнение которой находится из равенства |
n−1 = 0 |
и имеет вид: |
|
k |
|
= |
1 |
( |
Tу + Tд |
+ k |
|
)(1 + k |
|
k |
|
) . |
(4.43) |
||
у |
|
|
|
|
о.с. |
|
д |
||||||||
|
|
Tд |
|
|
kдTу |
|
|
о.с. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определим теперь с помощью гармонической линеаризации, как |
|||||||||||||||
влияет нелинейность |
|
( X ) |
на устойчивость |
системы. Из |
чисто |
||||||||||
физических соображений можно предположить, что эта нелинейность характеристики двигателя должна ухудшить условия устойчивости вследствие того, что при выходе скорости двигателя из линейной
100
