2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 6

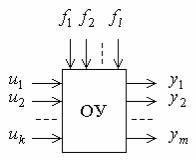
Рис. 6.1

Пусть y1, , ym обозначают выходные величины, u1, ,uk – сигналы управления или задающие воздействия и f1, , f l – возмущающие воздействия. Тогда уравнения многомерных стационарных линейных систем и объектов в общем случае можно записать в виде следующей системы:

к изображениям Лапласа, при нулевых начальных условиях получим систему алгебраических уравнений

(6.2)

где Yj(p) L[yj(t)],U j(p) L[uj(t)], Fj(p) L[fj(t)].

Для многомерных систем удобна матричная форма записи уравнений. Введем в рассмотрение матрицы

119

С их помощью (6.1) в матричной форме будет:

В (6.3) после умножения и сложения матриц в правой и левой частях получатся матрицы – столбцы. Приравняв их соответственные элементы, получим систему уравнений (6.1). Аналогично, выполнив указанные операции над матрицами и приравняв соответственные элементы матриц левой и правой частях матричного уравнения (6.4), получим систему (6.2).

Запись дифференциальных уравнений обьекта управления или системы управления в виде (6.3) или (6.4) называется уравнениями «вход-выход». Эти уравнения позволяют полностью описать статические и динамические свойства обьекта управления или системы управления.

Пример 6.1. Пусть исходная система дифференциальных уравнений имеет вид

120

(a0 p a1)y1 a2y2 b0 pu1 b1u2,

a3y1 (a4 p a5)y2 b2u2 .

В матричной форме, как нетрудно проверить, эта система записывается в виде

A(p)y(t) B(p)u(t),

где

6.1.2. Передаточные матрицы. Для описания многомерных систем и объектов, как и в случае одномерных систем, можно использовать передаточные функции. Передаточной функцией

Wiju(p) (в изображениях Лапласа) по j-му параметру управления и i-му выходу называют отношение изображения Лапласа выходной

Эту передаточную функцию можно вычислить следующим образом. В системе (6.2) приравниваем нулю изображения всех возмущающих воздействий и параметров управления, кроме U j(p).

Из полученной системы алгебраических уравнений находим решение Yi(p), а затем, разделив его на U j(p), получим искомую

передаточную функцию.

Аналогично определяют передаточную функцию Wijf (p) по j-му возмущающему воздействию и i-му выходу

В случае многомерных систем (объектов) для ее полного описания необходимо иметь m k передаточных функций по управлению и m l передаточных функций по возмущению. Эти передаточные функции записывают в виде матриц:

121

Пример 6.2. Пусть система (объект) описывается уравнениями

Wu(p) Wf (p) A 1(p).

6.1.3. Весовые или импульсные переходные матрицы. Пусть управляющий сигнал uj δ(t), а остальные управляющие сигналы и

возмущающие воздействия равны нулю. При этом решение (6.7) многомерной системы при нулевых начальных условиях обозначим

w1uj(t), w2uj(t), , wmju (t). Эти функции называют весовыми или импульсными переходными функциями. Функция wij(t) описывает

реакцию системы на i-м выходе при действии в точке приложения j-го параметра управления единичного импульса и называется импульсной переходной или весовой функцией по j-му параметру управления и i-му выходу.

123

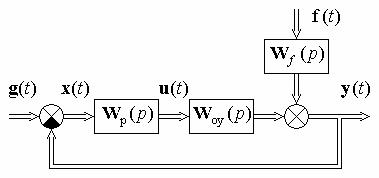
мой величины, u(t) – управляющих воздействий, f(t) – возмущений, Wоу(p) – передаточных функций объекта управления, Wf (p) –

передаточных функций для возмущений. Кроме того, введена прямоугольная матрица передаточных функций регулирующего устройства Wр(p), которая определяет используемые законы

регулирования. Она дает связь между изображениями управляющих величин и ошибок:

U(p) Wр(p)X(p).

Уравнения многомерной системы (рис. 6.2) могут быть получены действиями, аналогичными одномерному случаю.

125

координаты x1, , xn – фазовыми координатами. Вектор u называют вектором управления или просто управлением, а его координаты u1, ,uk – управляющими воздействиями. Вектор y называют вектором выхода, а его координаты y1, , ym– выходными координатами.

Под состоянием объекта (или динамической системы) понимается совокупность величин, полностью определяющих его динамику в данный момент времени. Обычно под состоянием объекта понимается совокупность значений выходных координат и их производных.

Будем определять состояние объекта (динамической системы) вектором x с компонентами x1, x2, , xn. Множество этих векторов составляет n мерное пространство состояний (фазовое пространство), которое может рассматриваться как абстрактное n-мерное пространство. Совокупность n линейно независимых векторов в этом пространстве образует базис. Каждая компонента xi является проекцией вектора состояния x на соответствующий вектор базиса.

Уравнения движения объекта можно привести к такому виду, в котором каждое из уравнений имеет первый порядок:

x Ax Bu;

y Cx,

где вход u и выход y представляют собой соответственно k-мерные

127