2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 6

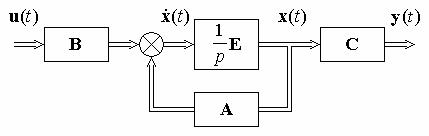
и m-мерные векторы, а размерность вектора x совпадает с порядком системы n; матрицы A, B и C являются числовыми.

Все составяющие векторов входа и выхода являются конкретными физическими величинами. Вектор же состояния может рассматриваться как некоторая абстрактная характеристика объекта. Физическая природа фазовых координат не является существенной. Координаты xi зависят от выбора базиса n-мерного линейного пространства состояний. Изменение базиса соответствует переходу к новым фазовым координатам xi , но не отражается на входных u и выходных y координатах, описывающих изменение конкретных физических величин.

Структурная схема модели вход-состояние-выход объекта в соответствии с уравнениями состояния (6.19) приведена на рис. 6.3.

Рис. 6.3. Структурная схема модели вход-состояние-выход

6.2.2. Преобразование дифференциальных уравнений к нормальной системе. Дифференциальные уравнения, разрешимые относительно старшей производной, всегда можно привести к нормальной системе. Рассмотрим, как преобразуются уравнения одномерной стационарной линейной системы управления.

Пусть система управления описывается уравнением

128

Учитывая их, из уравнения (6.26) получаем

Объединяя это уравнение с уравнениями (6.27), получаем нормальную систему

эквивалентную исходному уравнению (6.24). Выходная переменная системы управления и новые переменные связаны соотношением

(6.25)

Обратный переход от уравнений состояния к передаточной матрице объекта осуществляется по формуле

где E – единичная матрица.

Пример 6.3. Рассмотрим переход от уравнений вход-выход и передаточных функций к уравнениям состояния объекта.

Пусть, например, уравнение вход-выход имеет вид

Q(p)y R(p)u,

где Q(p) (p 1)(p 2); R(p) 1; n 2;m 1.

Передаточная функция:

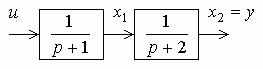
Структурная схема объекта приведена на рис. 6.4.

Рис. 6.4. Структурная схема объекта

Пусть x1 соответствует выходному сигналу первого звена, а x2 –

130

dx1 x2; dt

и уравнений состояния.

Решение. Рассмотрим движение самолета в продольной плоскости, совпадающей с плоскостью его симметрии. Это движение характеризуется следующими угловыми координатами: углом

атаки α, составленным вектором скорости и продольной осью x. Эти углы связаны кинематическим соотношением (см. рис. 1.9):

α θ.

Воздействиями, с помощью которых можно управлять движением самолета, являются изменение положения руля высоты δв и изменение тяги двигателей δр. В качестве выходных координат можно принять величину скорости V и один из углов: или θ.

132

Тогда исходные уравнения перепишутся в требуемой форме:

x1 n11x1 n12x2 n13x3 nрu1; x2 n21x1 n22x2 n23x3 x4;

x3 x4;

x4 (n31 n30n21)x1 (n30n22 n32)x2 n30n23x3(n30 n33)x4 nвu2;

y1 x1; y2 x3.

6.3. Управляемость и наблюдаемость

Математическое описание линейной динамической системы может быть выполнено с помощью дифференциальных уравнений «вход-выход», передаточной и весовой матриц, с помощью

и весовые матрицы, полученные при нулевых начальных условиях, могут не отражать некоторых динамических особенностей системы. Это становится особенно очевидно при рассмотрении свойств

описанием системы в терминах пространства состояний, т. е. записывая уравнения движения в виде

x Ax Bu;

(6.31)

y Cx.

134

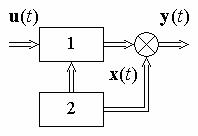
Рис. 6.5

Из (6.32) очевидно, что все фазовые координаты x2j

( j 1, 2, , n2) неуправляемы, так как на них не оказывает действие вход системы u ни непосредственно, ни через остальные координаты x1i (i 1, 2, , n1). Вектор фазовых координат x и матрицы A, B,C при этом имееют клеточную структуру

Свойство управляемости системы определяется парой матриц

системы x на основе знания реакции системы y на конечном интервале времени.

Система (6.31) называется полностью набдюдаемой, если она не эквивалентна системе вида

x1 A11x1 B1u;

а n1 n2 n. Другими словами, полностью наблюдаемой является система, для которой нельзя указать базис такой, чтобы фазовые координаты разбились на две группы, причем координаты второй группы x2 не входят ни в уравнения для координат первой группы, ни в алгебраические соотношения для выходных переменных y

(рис. 6.6).

136

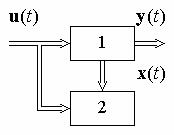
Рис. 6.6

Из (6.33) очевидно, что все фазовые координаты x2j

( j 1, 2, , n2) ненаблюдаемы, так как они не оказывают влияния на выход системы y ни непосредственно, ни через остальные координаты x1i (i 1, 2, , n1). Матрицы A, B,C при этом имеют вид

Свойство наблюдаемости системы определяется парой матриц A,C и не зависит от вида матрицы B.

Для решения вопроса о том, является система полностью управляемой и наблюдаемой или нет, воспользоваться непосредственно определениями, приведенными выше, затруднительно. Ответ на этот вопрос дают критерии управляемости и наблюдаемости, предложенные Р. Е. Калманом и позволяющие судить о свойствах системы без перехода к другим базисам на основе исходной формы записи уравнений (6.31).

Составим из матриц A, B матрицу

имеющей n строк и kn столбцов. Критерий управляемости формулируется следующим образом. Размерность n1 управляемой части равна рангу матрицы U. Как ивестно, ранг матрицы – это наивысший порядок минора матрицы, не равного нулю. Очевидно, что n1 n. Система является полностью управляемой, если ранг матрицы U равен n.

При n1 n система полностью управляема, при 0 n1 n – не полностью управляема и при n1 0 – полностью неуправляема.

Аналогичный критерий имеет место и для свойства наблюдаемости системы. Составим из матриц A,C матрицу

137